Pythonプログラミング（ステップ７・リスト・フーリエ級数）

周期的なデータ

連続的な時間$t$の各点で値を持つようなデータの系列 $x(t)$を考える。 ただし、基本的な周期$T$が存在して、 $$ x(t+T) = x(t) \tag{1} $$ であるとしよう。 例えば、ある地点の気温の変動を考えるけれども、毎年、完全に同じ変動を繰り返す（$T$は1年）、といったケースである。 厳密に考えれば、完全に同じパターンが繰り返されるような現象はあり得ないとも言えるので、これは一種の理想化ではあるが、 範囲を区切るなどすれば、ほぼそれに近い状況はいくつも見つけることができるだろう。 例えば、一定の音程で発声している声や楽器の音信号や、あるいは、$t$を空間座標と読み替えれば、結晶中の原子の位置も、こうした例の一種とみなせる。

周期$T$を持つような関数の代表は、なんと言っても、正弦関数と余弦関数、 $$ \sin\left(\frac{2 \pi n}{T} t\right), \;\; \cos\left(\frac{2 \pi n}{T} t\right) $$ であろう。ここで、$n$は任意の整数をとり得る。 $n=0$の場合は定数関数になるが、もちろん、それも周期関数の一種である。

フーリエ級数

周期$T$の任意の関数は、周期が$T/n$の正弦関数と余弦関数の重ね合わせ $$ x(t) = c + \sum_{n=1}^{\infty} \left[ a_n \sin\left(\frac{2 \pi n}{T} t\right) + b_n \cos\left(\frac{2 \pi n}{T} t\right) \right] \tag{2} $$ で表現できることが証明されている。この級数は、発見者である数学者フーリエにちなんで、フーリエ級数と呼ばれている。 言い方を変えると、どのような周期関数$x(t)$でも、複数の正弦波に必ず「分解」することができる。 その数学的な証明は専門書にあたっていただくことにして、以下で、その「使い方」についてみてゆくことにしよう。

ここで天下り的ではあるが、$m=1,2,\cdots$ について、区間$T$での以下の積分について $$ \begin{eqnarray} \int_0^T \sin\left(\frac{2 \pi n}{T} t\right) \sin\left(\frac{2 \pi m}{T} t\right) dt & = & \frac{T}{2} \delta_{m,n} \\ \int_0^T \sin\left(\frac{2 \pi n}{T} t\right) \cos\left(\frac{2 \pi m}{T} t\right) dt & = & 0 \\ \int_0^T \cos\left(\frac{2 \pi n}{T} t\right) \cos\left(\frac{2 \pi m}{T} t\right) dt & = & \frac{T}{2} \delta_{m,n} \end{eqnarray} \tag{3} $$ であることを用いると（$\delta_{n,m}$はクロネッカーのデルタ）、(2)式の両辺に正弦関数や余弦関数をかけて積分することで、 $$ \begin{eqnarray} \int_0^T x(t) \sin\left(\frac{2 \pi m}{T} t\right) \, dt = a_m \frac{T}{2} \\ \int_0^T x(t) \cos\left(\frac{2 \pi m}{T} t\right) \, dt = b_m \frac{T}{2} \end{eqnarray} \tag{4} $$ 加えて、三角関数の周期性から $$ \int_0^T x(t) dt = T c \tag{5} $$ も明らかである。

以上をまとめ直すと、フーリエ級数の係数は $$ \begin{eqnarray} c & = & \frac{1}{T} \int_0^T x(t) dt \\ a_n & = & \frac{2}{T} \int_{0}^{T} x(t) \sin\left(\frac{2 \pi n}{T} t\right) \, dt \\ b_n & = & \frac{2}{T} \int_{0}^{T} x(t) \cos\left(\frac{2 \pi n}{T} t\right) \, dt \end{eqnarray} \tag{6} $$ で与えられる。 ただし、関数の周期性から、積分範囲は $$ \int_{t_0}^{t_0 + T} \cdots dt $$ であれば、$t_0$の選び方は任意である。

矩形波の分解

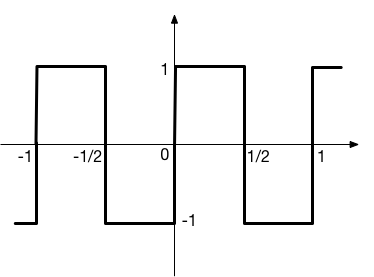
では、$x(t)$として、図のような周期$1$の矩形波を考えてみよう。このような角張った波形が、本当に正弦関数（と余弦関数）の重ね合わせで表現できるのだろうか。

フーリエ級数の係数を求めてみると、 まず、波形の対称性から、明らかに $$ c = 0 $$ である。 さらに、 $$ a_n = 2 \int_0^{1/2} \sin(2 \pi n t) dt + 2 \int_{1/2}^{1} (-1) \sin(2 \pi n t) dt = \begin{cases} 0 & (n \textrm{:even}) \\ \frac{4}{n \pi} & (n \textrm{:odd})\\ \end{cases} $$ $$ b_n = 2 \int_0^{1/2} \cos(2 \pi n t) dt + 2 \int_{1/2}^{1} (-1) \cos(2 \pi n t) dt = 0 $$ となることが分かる。

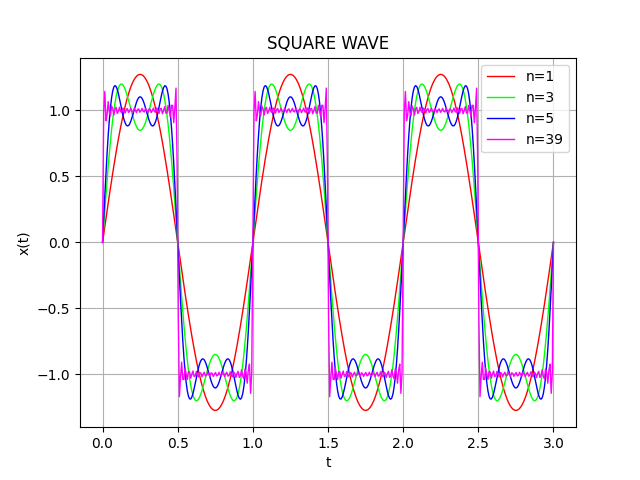
このフーリエ級数を1, 3, 5, そして 39次までで打ち切った際の様子をプロットするコードの例と出力例を以下に示す。 項の数が大きくなるについて、矩形波に近づく様子が観察できる。

# coding: utf-8

import numpy as np
import math
import matplotlib.pyplot as plt


t = np.linspace(0,3,400)

x1 = 4/(1*np.pi)*np.sin(2*np.pi*1*t)
x3 = 4/(1*np.pi)*np.sin(2*np.pi*1*t) + 4/(3*np.pi)*np.sin(2*np.pi*3*t)
x5 = 4/(1*np.pi)*np.sin(2*np.pi*1*t) + 4/(3*np.pi)*np.sin(2*np.pi*3*t) +  4/(5*np.pi)*np.sin(2*np.pi*5*t)

xn = np.zeros(shape=(t.shape[0],))
for n in range(1,40,2):
    xn += 4/(n*np.pi)*np.sin(2*np.pi*n*t)


plt.title("SQUARE WAVE")
plt.plot(t, x1, color=(1.0,0.0,0.0), linewidth=1.0, label="n=1")
plt.plot(t, x3, color=(0.0,1.0,0.0), linewidth=1.0, label="n=3")
plt.plot(t, x5, color=(0.0,0.0,1.0), linewidth=1.0, label="n=5")
plt.plot(t, xn, color=(1.0,0.0,1.0), linewidth=1.0, label="n=39")
plt.legend()
plt.xlabel('t')
plt.ylabel('x(t)')
plt.grid(True)
plt.show()

　練習：のこぎり波の分解

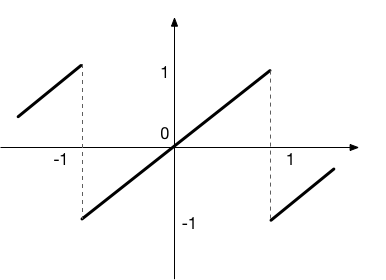
矩形波の例に倣って、のこぎり波（下図）をフーリエ級数で近似・表示してみなさい

複素関数を使った表現

複素指数関数を使うと、(2)式はさらにすっきりと $$ x(t) = \sum_{n=-\infty}^{\infty} c_n \exp\left( i \frac{2\pi n}{T} t\right) $$ と表現することができる。

オイラーの公式から $$ \begin{eqnarray} \sum_{n=-\infty}^{\infty} c_n \exp\left( i \frac{2\pi n}{T} t\right) = \sum_{n=-\infty}^{\infty} c_n \left[ \cos\left( \frac{2\pi n}{T} t \right) + i \sin\left( \frac{2\pi n}{T} t \right) \right] \\ = c_0 + \sum_{n=1}^{\infty} \left[ i (c_n - c_{-n}) \sin\left( \frac{2\pi n}{T} t \right) + (c_n + c_{-n}) \cos\left( \frac{2\pi n}{T} t \right) \right] \end{eqnarray} $$ したがって、式を見比べると、係数の間には $$ \begin{eqnarray} c & = & c_0 \\ a_n & = & i (c_n - c_{-n}) \\ b_n & = & c_n + c_{-n} \end{eqnarray} $$ という対応が成り立つ。 連立方程式を解いて $$ \begin{eqnarray} c_n & = & \frac{b_n - i a_n}{2} \\ c_{-n} & = & \frac{b_n + i a_n}{2} \\ \end{eqnarray} $$ このことから、$c_n$と$c_{-n}$は複素共役 $$ c_{-n} = c^*_n $$ の関係にあることがわかる。

　解説: 一筆書き

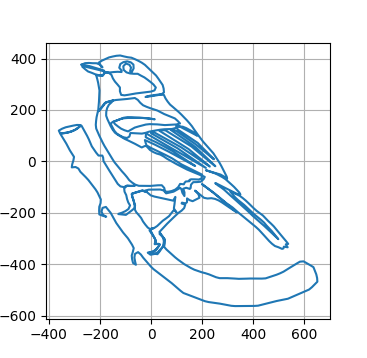
写真の鳥（シジュウカラ）の外形を「閉じた一筆書き」でトレースして、座標に変換したデータファイル great-tit-drawing.txtを用意した。 このデータファイルでは、一筆書きの全体の線の長さを1024等分し、それぞれの点のx座標とy座標の値がリストされている。

以下のPythonコードを使って、座標を読み出してプロットすると、鳥の一筆書きが表示される。

# coding: utf-8

import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt("great-tit-drawing.txt")
xpos = data[:,0]
ypos = data[:,1]
plt.plot(xpos, ypos)
plt.grid()
plt.show()

これらの線分はループを形成しているので、（線分長の関数としての）ｘ座標、y座標共に、周期的であることは明らかである。 そして、これを一種の「時系列」と見なせば、この節で述べたフーリエ級数の考え方がそのまま適用できる。

ただし、データ点は有限であることから、データ点の「幅」よりも細かい変化についての情報はもともと含まれておらず、 そのような場合は、有限の項数を持つ級数（すなわち、有限個の正弦、余弦関数の和）でデータを表現できることがわかっている。 これは、離散フーリエ変換（discrete Fourier transform; DFT)と呼ばれている。

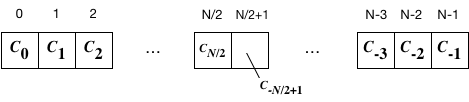
NumPyに含まれる np.fft.fft()関数を使うと、$N$データ点 $x_0, x_1, x_2, \cdots, x_{N-1}$ についての（離散的）フーリエ級数 $$ x_k = \frac{1}{N} \sum_{n=-N/2}^{N/2} c_n \exp\left(i \frac{2 \pi n}{N} k \right) $$ の係数 $c_n$が、サイズ$N$の配列として得ることができる。 計算結果として返される配列には、以下の図のような順に係数が格納されている：

NumPyのDFTの機能を用いて展開係数 $c_n$ を求め、 その後、限られた（低次の）項のみを用いて式(2)に従ってデータを「復元」するコードを作成してみた。 変数 nlimが、フーリエ級数の打ち切り次数に対応する。

# coding: utf-8

import numpy as np
import matplotlib.pyplot as plt

data = np.loadtxt("great-tit-drawing.txt")
xpos = data[:,0]
ypos = data[:,1]

X = np.fft.fft(xpos)
Y = np.fft.fft(ypos)

nlim=64

N = X.shape[0]
s = np.arange(0,N,1.0)
x = X[0] * np.cos(2*np.pi*0.0/N*s)/N
y = Y[0] * np.cos(2*np.pi*0.0/N*s)/N
for n in range(1,nlim+1):
    xan = (X[n] - X[N-n]) * (0.0 + 1.0j)
    xbn = (X[n] + X[N-n])
    yan = (Y[n] - Y[N-n]) * (0.0 + 1.0j)
    ybn = (Y[n] + Y[N-n])
    x = x + xan * np.sin(2*np.pi*n/N*s)/N + xbn * np.cos(2*np.pi*n/N*s)/N
    y = y + yan * np.sin(2*np.pi*n/N*s)/N + ybn * np.cos(2*np.pi*n/N*s)/N

plt.plot(np.real(x), np.real(y),label='nc='+str(nlim))
plt.grid()
plt.legend()
plt.show()

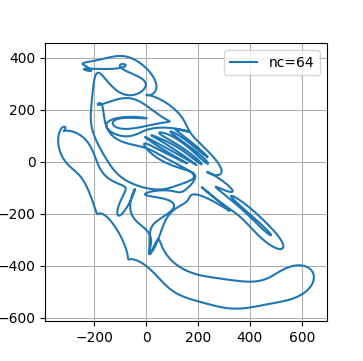
64次までで打ち切った場合の例を以下に示す。細かい線は消されて（省略されて）しまっている一方で、図形の概要は再現されていることが判る。

フーリエモードの「省略」によって得られるパターンは、どこかしら、ピカソの動物の線描に似ているようにも思われる。 この偉大な画家が、細かい線の変化は無視し、なだらかな曲線のみを残すことによって、対象物のミニマルな表現を追求したとすれば、 こうした類似性はあながち不思議なことではないのかもしれない。

　練習

打ち切り次数を1, 2, 3と増やしながら図形の変化を確かめ、「そうなる理由」について考察してみなさい。