Pythonプログラミング(ステップ7・統計的検定・ウィルコクソンの順位和検定)
このページでは、2セットのデータ間で分布の代表値に違いがあるかどうかを検定するノンパラメトリックな方法について考える。
2グループの試験の結果の違い
同じ試験を2つのグループに対して実施して、違いがあるかどうかを検討したい。 試験の結果は点数化できるものとすると、ナイーブな発想としては、両群の平均値を求め、その大小を議論すれば良さそうである。 しかしながら、平均の大小に意味があるかどうかは慎重に吟味しなければならない。 ここでは、点数が正規分布すると仮定できない(サンプル数が少なすぎて正規性をチェックできない、あるいは、そもそも正規分布から 大きく偏っている)場合を想定して、その方法について考えてみたい。
2つのグループ A, Bについて、グループ1の人数を$n_A$で、それぞれの点数が$\{x_i\}$ ($i=1,\cdots,n_A$)、 グループ2の人数が$n_B$で、点数が$\{y_j\}$ ($j=1,\cdots,n_B$)であったとする。 ここで、もし2つのグループに全く違いが無ければ、2つを併せて一群と見なしても、統計的な性質に違いは生じないはずである。
そこでまず、$n_A + n_B$人分の全データを併せて、小さい順に並べ替え、点数の低い順に順位を付けておく。
そして、グループを特長づける量として、片方のグループ(ここではグループAとする)の受験者の、 併合したグループ内での順位の和を考える。
順位を通してグループを特徴づけることで、点数分布の正規性をあらかじめ仮定しなくても済む。 ここで、「正規性を仮定する」とは、母集団の特徴が平均と分散で表されると仮定するという意味で、 平均と分散というパラメータの値と差異が議論の中心となる。 これに対して、順位を用いる方法はノンパラメトリックな(パラメータに依らない)手法のひとつであり、 より広い対象についての議論が可能となる。 ここで紹介するのは、ウィルコクソンの順位和検定(Wilcoxon rank sum test)とよばれる方法である。
順位和の計算例
順位和の場合の数
2つのグループに違いがなければ、全体の中である順位を占ている人がどちらのグループに属していても構わない。 以下では簡単のため、順位は全て異なる(同順位はない)場合を考える。
例えば、グループAが6人、グループ2も6人の、全体で12名の場合を考えると、グループAの順位和の現れ方として
1 + 2 + 3 + 4 + 5 + 6 = 21 1 + 2 + 3 + 4 + 5 + 7 = 22 1 + 2 + 3 + 4 + 6 + 7 = 23 1 + 2 + 3 + 4 + 5 + 8 = 23 1 + 2 + 3 + 4 + 5 + 9 = 24 1 + 2 + 3 + 4 + 6 + 8 = 24 1 + 2 + 3 + 5 + 6 + 7 = 24 ... 6 + 8 + 9 + 10 + 11 + 12 = 56 7 + 8 + 9 + 10 + 11 + 12 = 57
がすべて等しい可能性を持っていることになる。
順位和を $S$、グループAの人数を $k$、可能な順位の最大値を $m$ とすれば、 順位和が $S$ となるような場合の数は
『値が$m$以下の、$k$個の異なる自然数の和が$S$となるような組み合わせの数』
に等しい。すなわち、場合の数は、自然数の加算分割問題の一種と解釈できる。
その計算方法は、 参考書 の『4.6 自然数の分割』に述べられているので、ここでは詳細は割愛する。 以下は参考書中の アルゴリズム20 をPythonで記述して、$S$ の加算分割を求め、表示するコードの例である:
# Algorithm 20: 加算分割問題を解く
# coding: utf-8
def rank_sum(s, k, m):
if s<1:
return [ ],0
if m<k:
return [ ],0
if k==1:
if s<=m:
return [[s]],1
else:
return [ ],0
ell = [ ]
c = 0
t = min(m, s-k*(k-1)//2)
while True:
ellprime,cprime = rank_sum(s-t,k-1,t-1)
for g in ellprime:
ell.append(g + [t])
c = c + cprime
t = t - 1
if k*t < s + k*(k-1)//2:
break
return ell,c
# メイン部
s = int(input('S='))
k = int(input('k='))
m = int(input('m='))
ell,c = rank_sum(s,k,m)
print('場合の数=',c)
for e in ell:
print(e)
順位和の分布形
1位から $n_A + n_B$ 位までの順位を、AグループとBグループに割り付けるやり方は、全部で
$$
{n_A + n_B \choose n_A } =
\frac{(n_A + n_B)!}{n_A! \; n_B!}
$$
通りである。
その中で、Aの順位和(rank sum)が $s$ であるような組み合わせの割合(順位和の確率分布)を求め、表示するPythonコードを以下に示す。
変数 m が $n_A + n_B$、k が$n_A$(または$n_B$)に対応する。
# coding: utf-8
import math
import matplotlib.pyplot as plt
def rank_sum(s, k, m):
if s<1:
return [ ],0
if m<k:
return [ ],0
if k==1:
if s<=m:
return [[s]],1
else:
return [ ],0
ell = [ ]
c = 0
t = min(m, s-k*(k-1)//2)
while True:
ellprime,cprime = rank_sum(s-t,k-1,t-1)
for g in ellprime:
ell.append(g + [t])
c = c + cprime
t = t - 1
if k*t < s + k*(k-1)//2:
break
return ell,c
# メイン部
m = 12
k = 6
SS = k*(k+1)//2
SE = k*(2*m-k+1)//2
rs=[ ]
n_rs=[ ]
n_norm=[ ]
sum=0
tot=math.factorial(m)/(math.factorial(k)*math.factorial(m-k))
mu = k * (m+1)/2
sigma = math.sqrt(k*(m-k)*(m+1)/12)
for s in range(SS,SE+1):
ell,c = rank_sum(s,k,m)
rs.append(s)
n_rs.append(c)
g = tot/(math.sqrt(2*math.pi)*sigma) * math.exp(-(s-mu)**2/(2*sigma**2))
n_norm.append(g)
q = 1 - sum/tot
sum += c
p = sum/tot
print(s,p,q)
plt.bar(rs, n_rs, color=(1.0,0,0.0), label="m,k="+str(m)+","+str(k))
plt.plot(rs, n_norm, color=(0.0,0,1.0), label="Normal Approx.")
plt.xlabel('Rank Sum')
plt.ylabel('N')
plt.legend()
plt.grid(True)
plt.show()
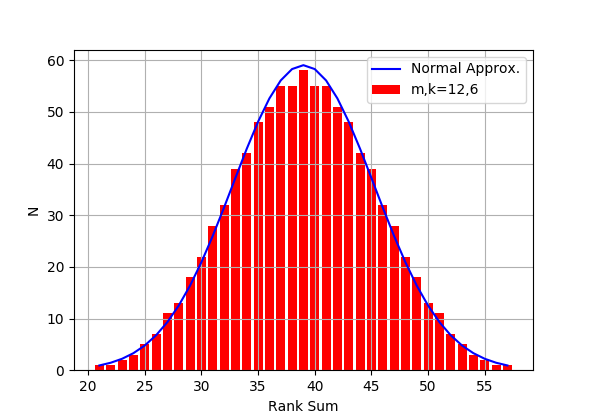
上のコードで表示した順位和の分布を以下に示す:
グループのメンバーの数が大きければ、この分布は平均が $$ \mu = \frac{n_A (n_A + n_B+1)}{2} $$ 分散が $$ \sigma^2 = \frac{n_A n_B (n_A + n_B + 1)}{12} $$ の正規分布で近似できることが知られている(グラフ中、青色の実線でプロット)。
順位和による2グループの違いの検定
上記のコードを実行すると、以下のような数値の表が出力される。 左から、順位和、順位和がそれ以下である確率、順位和が以上となる確率、 をそれぞれ表す。
21 0.0010822510822510823 1.0 22 0.0021645021645021645 0.9989177489177489 23 0.004329004329004329 0.9978354978354979 24 0.007575757575757576 0.9956709956709957 25 0.012987012987012988 0.9924242424242424 26 0.020562770562770564 0.987012987012987 27 0.032467532467532464 0.9794372294372294 .... 50 0.9675324675324676 0.04653679653679654 51 0.9794372294372294 0.03246753246753242 52 0.987012987012987 0.02056277056277056 53 0.9924242424242424 0.012987012987012991 54 0.9956709956709957 0.007575757575757569 55 0.9978354978354979 0.0043290043290042934 56 0.9989177489177489 0.0021645021645021467 57 1.0 0.0010822510822511289
このとき、帰無仮説として『2つのグループは同じ点数分布を持つ集団からのサンプルである』を、 対立仮説として『2つのグループの点数分布には差があった』をそれぞれ設定し、 有意水準を 0.01 と置いたと想定してみよう。
その場合、分布の片側で 0.005 以下の確率となるのは、順位和が 23以下 および、順位和が 55以上の領域である。 すなわち、グループAの順位和が 23以下、または55以上であれば、有意水準 0.01 で帰無仮説は棄却される。
 練習:ウィルコクソンの順位和検定
練習:ウィルコクソンの順位和検定
ある試験をA大学とB大学とで実施したところ、各学生の点数はそれぞれ以下のようであった。
A大学 68 87 73 90 83 B大学 55 98 80 77 61 72
試験の結果に優位な差があるかかどうかを、ウィルコクソンの順位和検定(両側検定)を使って分析しなさい。
 ヒント:SciPyの利用
ヒント:SciPyの利用
このページで述べた Wilcoxonの順位和検定は、Mann-WhitneyのU検定と呼ばれる方法と、本質的に同等である。
SciPyのライブラリにはMann-WhitneyのU検定を行う関数 mannwhitneyu()が用意されている。
ただし、
マニュアルによれば、
それぞれのサンプル数が20より大きな場合に使用が制限されている。
# coding: utf-8
from scipy.stats import mannwhitneyu
x = [68, 32, 85, 76, 73, 84, 90, 79, 83, 41, 95, 69, 80, 77, 68, 78, 85, 73, 84, 56, 67]
y = [87, 98, 80, 82, 63, 78, 79, 87, 93, 69, 88, 91, 76, 68, 89, 93, 76, 99, 78, 80]
u,pval = mannwhitneyu(x,y,alternative='two-sided')
print('U=',u)
print('p=',pval)