Pythonプログラミング(ステップ7・カイ二乗検定・独立性)
このページでは、独立性についてのカイ二乗検定について考える。(このページは作成中)
独立性の検定
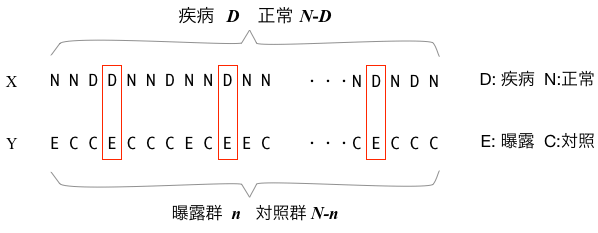
化学物質や放射線等による曝露の影響を調べるため、疫学的な調査を行っているとしよう。 曝露を受けたグループと、対照群(コントロール)について、疾患が認められる人数と正常な人の人数をそれぞれ以下のような分割表(contingency table)にまとめたとしよう ($a, b, c, d$はそれぞれの人数で、全体で $a+b+c+d=N$人が調査の対象であったとする)。
| 疾患有 | 正常 | 計 | |
| 曝露群 | $a$ | $b$ | $a+b$ |
| 対照群 | $c$ | $d$ | $c+d$ |
| 計 | $a+c$ | $b+d$ | $N$ |
ここで、$N$人のうち、疾患有を $D=a+c$ 人、暴露群の人数を $n=a+b$ とおくと、暴露群の中で疾患有りの人数($k$とする)が決まれば、上の表の欄は全て一意に決まってしまう。 その意味で、このデータの自由度は1(1つの確率変数で表現できる)と言える。
| 疾患有 | 正常 | 計 | |
| 曝露群 | $k$ | $n - k$ | $n$ |
| 対照群 | $D-k$ | $N-n-D+k$ | $N-n$ |
| 計 | $D$ | $N-D$ | $N$ |
もしも、疾患と曝露が全く無関係(独立)であったとすると、この表の$k$はどのような確率分布に従うべきだろうか?
$N$人の中から曝露群に$n$人を割り当てる場合の数は$N\choose{n}$である。その中で、疾患のある$D$のうち$k$人と、疾患の無い$N-D$人のうちの$n-k$人をそれぞれ曝露群に割り当てる 場合の数は ${D\choose{k}} {{N-D}\choose{n-k}}$ 通りある。 従って、独立性を仮定した場合に表の左上が$k$であるような確率は、 $$ p(k) = \frac{{D\choose{k}} {{N-D}\choose{n-k}}}{{N}\choose{n}} \tag{1} $$ であることが分かった。この分布は超幾何分布 (hypergeometric distribution)と呼ばれている。
これを元の表記$a, b, c, d$を使って表すと $$ \frac{(a+b)! \ (c+d)! \ (a+c)! \ (b+d)!}{N! \ a!\ b!\ c!\ d!} \tag{2} $$ となり、Fisherの正確確率検定ではこちらの表式が使われることが多い。
式(1)の超幾何分布の平均と分散は $$ \mu = \sum_{k=0}^{n} k \ p(k) = \frac{n D}{N} $$ $$ \sigma^2 = \sum_{k=0}^{n} k^2 p(k) - \mu^2 = \frac{n(N-n)}{N-1} \frac{D}{N} \frac{N-D}{N} $$ となる(導出は省略)。 また、$N$, $k$共に十分大きな数のとき、超幾何分布は正規分布に漸近することが分かっている。 すると、 $$ \frac{k - \mu}{\sigma} $$ は平均0、分散1の正規分布に従うので、その2乗、すなわち $$ \chi^2 = \frac{(k - \mu)^2}{\sigma^2} $$ は、自由度1のカイ2乗分布に従うことになる。
ここで、$k=a, n=a+b, D=a+c, N=a+b+c+d$を入れ、$N \simeq N-1$とおいて式を整理すると、 $$ \chi^2 = \frac{N (ad-bc)^2}{(a+b)(a+c)(b+d)(c+d)} \tag{3} $$ が得られる。
一方で、統計学の教科書には、分割表の$i$行 $j$列の平均値を $E_{ij}$、データを $O_{ij}$ とするときにカイ二乗統計量は $$ \chi^2 = \sum_{ij} \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \tag{4} $$ で計算できる、と書かれている。 上の表の場合に、それぞれの項を具体的に書き下すと $$ \chi^2 = \frac{\left(a - \frac{(a+b)(a+c)}{N^2} N \right)^2}{\frac{(a+b)(a+c)}{N^2} N} + \frac{\left(b - \frac{(a+b)(b+d)}{N^2} N \right)^2}{\frac{(a+b)(b+d)}{N^2} N} + \frac{\left(c - \frac{(a+c)(c+d)}{N^2} N \right)^2}{\frac{(a+c)(c+d)}{n^2} N} + \frac{\left(d - \frac{(b+d)(c+d)}{N^2} N \right)^2}{\frac{(b+d)(c+d)}{n^2} N} $$ となるが、(それなりに退屈な計算をして)式を整理すると、これは式(3)と完全に一致することがわかる。 すなわち、式(4)のやり方で求めた量も、自由度1のカイ二乗分布に従う。
同様に、分割表の行の数が$r$、列の数が $c$の場合には、式(4)の統計量は、自由度 $(r-1) \times (c-1)$ のカイ二乗分布に従う。 2行2列の場合は $(2-1) \times (2-1)$ なので、自由度は1となり、上記の計算と整合する。
 解説:分割表のシミュレーション
解説:分割表のシミュレーション
$N$個の要素から成るXとYの2つのリストがあって、Xには「疾患有り」を表すDが$D$個、「無し」を表すNが$N-D$個、 他方Yは、暴露群に割当られたことを示すEが$n$、対照群を表すCが$N-n$、それぞれ割当られているような状況を考える。 XとYの要素をランダムに組み合わせたときに、XとYがD-Eになっているような組(図の赤枠)の数が、上記の説明の$k$の値に対応するはずだ。
ランダムな系列を生成し、D-E のペアの個数を $k$ とする。
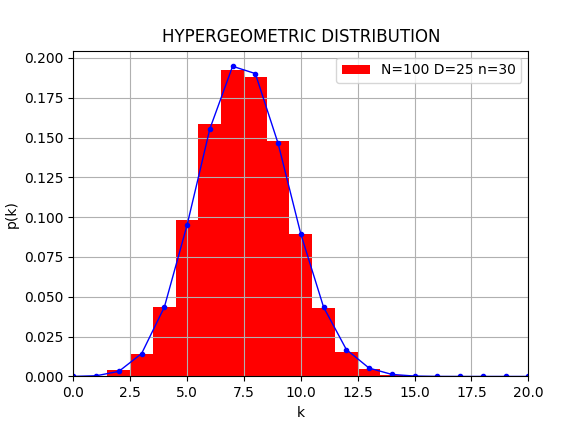
そこで、配列のシャッフル機能を使って、実際に何度も組み合わせを行い、得られた$k$の分布を表示するPythonコードの例を以下に示す。 ただし、リストの要素に記号ではなく数値(0か1)を使ってコーティングしている。 併せて、式(1)の確率分布もプロットするようになっている。
np.concatenate([配列1, 配列2]) は2つ配列を結合した配列を生成
np.random.shuffle(配列) は配列の内容をランダムに入れ替える
# coding: utf-8
import math
import random
import numpy as np
from scipy.stats import hypergeom
import matplotlib.pyplot as plt
ntrial=10000
N = 100
D = 25
n = 30
# 0 がD個、1が N-D個の配列を生成
x = np.concatenate([np.zeros(D,int), np.ones(N-D,int)])
# 0 がn個、1が N-n個の配列を生成
y = np.concatenate([np.zeros(n,int), np.ones(N-n,int)])
tab = []
for _ in range(ntrial):
np.random.shuffle(x) # 配列要素をランダムに並べ替える
np.random.shuffle(y)
k=0
for i in range(N):
if x[i]==0 and y[i]==0: # 両方0のペアをカウントする
k=k+1
tab.append(k)
rv = hypergeom(N, n, D)
xaxis = np.arange(0, n+1)
pmf = rv.pmf(xaxis)
plt.title("HYPERGEOMETRIC DISTRIBUTION")
plt.hist(tab, bins=xaxis-0.5, density=True, color=(1.0,0,0.0), label="N="+str(N)+" D="+str(D)+ " n="+str(n))
plt.plot(xaxis,pmf,'.-',color=(0.0,0,1.0), linewidth=1.0)
plt.xlim(0,20)
plt.legend()
plt.xlabel('k')
plt.ylabel('p(k)')
plt.grid(True)
plt.show()
赤いバーがシミュレーション結果、青線が対応する超幾何分布。
病因となっている遺伝子を見つける
我々の遺伝情報はDNA上の1次元的な文字(塩基の種類)として記憶されているが、その中の「単語」あるいは「文」に相当するのが遺伝子である。 ヒトの場合、2万以上の遺伝子が現在見つかっており、それぞれの遺伝子の型がさまざまな形質を決める要因になっている。 そして、その中には遺伝病も含まれる。
ここで、ある遺伝子座 X に可能な遺伝子が G, T の二種類であるとき、ある疾患が遺伝子 G に由来するかどうか調べたい。 ただし、G は顕性(優性)である(相同染色体の少なくとも片方にGがあれば、それが表現される)場合について考える。 簡単のため、G の他に対立遺伝子は T のみとするが、複数の対立遺伝子が可能な場合は、Tを「G以外の遺伝子」と考えればよい。
そこで、疾患を持ったグループ $R$ 人と、無作為に選んだグループ $S$ 人(対照群)について、遺伝子座 X の解析を行って、比較することにした。
調査の結果、遺伝型毎の人数の表を得ることができる。
表1
| GG | GT | TT | ||
| 疾患群 | $r_0$ | $r_1$ | $r_2$ | $R$ |
| 対照群 | $s_0$ | $s_1$ | $s_2$ | $S$ |
| 計 | $n_0$ | $n_1$ | $n_2$ | $N$ |
このデータをもとに、遺伝子の数についての2×2の表にまとめ直すことができる:
表2
| G | T | ||
| 疾患群 | $2 r_0 + r_1$ | $r_1 + 2 r_2$ | $2 R$ |
| 対照群 | $2 s_0 + r_1$ | $s_1 + 2 s_2$ | $2 S$ |
| 計 | $2 n_0 + n_1$ | $n_1 + 2 n_2$ | $2 N$ |
遺伝子Gが疾患に関係がない(独立)との帰無仮説を立て、 式(3)に従ってカイ二乗統計量を求め、Gが疾患にとって統計的に有意かどうかを評価することができる。
 練習:分割表の検定
練習:分割表の検定
表1の各欄の数値を入力すると、Gと疾患が無関係と仮定した場合のカイ二乗分布統計量に対するp値を出力するコードを書いてみなさい。
 ヒント
ヒント
表2のデータに対して、式(3)に従ってカイ二乗統計量を求め、分布関数を積分すればよいが、 SciPyライブラリの中には各種の統計計算を行ってくれる関数が多数用意されているので、そちらを使うと便利である。 以下は、chi2_contingency関数を使って、分割表のカイ二乗統計量やp値を求めるコードの例である:
# coding: utf-8
from scipy.stats import chi2_contingency
table=[[180,20],
[380,7]]
chi2, pval, dof, expctd = chi2_contingency(table)
print("p-value:",pval)