Pythonプログラミング（ステップ７・統計的仮説検定）

このページでは、統計的仮説検定の考え方について復習する。

背理法による証明

$\sqrt{2}$が無理数である（有理数でない）ことを証明するには、通常、背理法(proof by contradiction)が使われる。 考え方のアウトラインは、

1. 2の平方根が有理数である（$m,n$を自然数として、 $\sqrt{2}=m/n$ と置ける）と仮定する
2. この仮定のもとで、数学的な矛盾が生じることを示す
3. 矛盾が生じたのは仮定に誤りがあった、すなわち、$\sqrt{2}$ を有理数とおいたことによる
4. 無理数とは有理数でない数であるから、$\sqrt{2}$が無理数であることが証明できた

となる。

【矛盾の示し方の例】$m, n$を自然数として、$\sqrt{2}=m/n$とおいて両辺を二乗し変形すると、$2n^2 = m^2$となる。両辺を因数分解すると、左辺は因数として素数2を余計にひとつ含む。 素因数分解の一意性から、 両辺の因数2の数は等しくなければならないから、これは矛盾。

背理法による証明では、矛盾点を示すことに失敗したとしても、最初に置いた仮定が正しいわけではないことに注意したい。

確率を使った背理法：統計的仮説検定

統計的仮説検定も同じような発想で、『何々であること』を主張するために、『何々でなかった』とすると生じる確率的な矛盾を示す方法が採られる。

例えば、ある化学物質に毒性があるか無いかを確かめるため、曝露群と対照群それぞれについて実験データが得られたとしよう。 このとき、得られたデータ（数値）から、毒性の有無を推論するために、以下のようなステップを踏むのが一般的である。

1. 確かめたい主張『暴露群と対照群とで、暴露群のほうが疾患が生じる比率が高い』を設ける。これを対立仮説（alternative hypothesis）と呼ぶ。
2. それが正しくないとしたら対立仮説が支持できるような（確率的な矛盾を引き出すための）仮説を設ける。これを帰無仮説（null hypothesis）と呼ぶ。 例えば、『暴露群と対照群とでは疾患の率に差は無い』。
3. 帰無仮説が正しい状況の確率モデルを考え、そのモデルに基づいて、観測されたデータが見いだされる確率を見積もる。
4. その確率が十分小さければ（例えば5%以下）帰無仮説が棄却され、対立仮説が採択される。

ここで、帰無仮説が棄却できない（検定結果がが有意でなかった）場合は、帰無仮説が支持されたわけではないことに注意する。 というのは、帰無仮説が設定したモデルよりもデータをより合理的に（高い尤度で）説明するモデルがあるはずなので、 棄却されなかったことを以て、帰無仮説を「正しい」とすることはできないからだ。 その意味で、「帰無仮説を採択する」という表現を使うべきではない。

二項検定

ここで、比較的シンプルなモデルを使って考察できる統計的仮説検定の例を考えてみよう。

サッカー試合のコイントス等で使うためのコインに偏りが生じないか調べるため、コインを何度もトスしてみたところ、表が11回、裏が19回出た。

ここで、対立仮説として『このコインは表と裏が出る確率に偏りがある』を設定してみる。 帰無仮説は『このコインの裏表が出る確率は等しい』となる。

ここで、有意水準を$\alpha=0.05$に設定する。ただし、以下に述べるように、離散的な事象を扱うため、 棄却域の確率がちょうど0.05となるように範囲を設定することはできない。

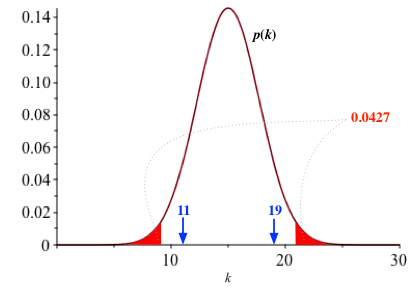
帰無仮説の下で、表が$k$回、裏が$30-k$回出る確率は、二項分布を使って、 $$ p(k) = {30 \choose k} \left( \frac{1}{2} \right)^{30} = \frac{30!}{k! \, (30-k)!} \frac{1}{2^{30}} $$ となる。

表裏の出方に偏りがあるというのは、表が少なく出る場合と、表が多く出る両方の場合が考えられるから、 分布の両裾の面積を合わせると有意水準となるような$k$の範囲を求めておく必要がある（両側検定）。 $p(k)$は平均値の両側で対称なので $$ \sum_{k=0}^x p(k) + \sum_{k=n-x}^n p(k) \le 0.05 $$ となるような最大の$x$を求める。以下のようなコードを使って調べてみると

# coding: utf-8

from scipy.stats import binom

n = 30
alpha=0.05

for k in range(n+1):
    p1 = binom.cdf(k, n, 0.5)
    p2 = 1.0-binom.cdf(k, n, 0.5) + binom.pmf(k, n, 0.5)
    print("p(",k,"): ",p1,p2)

$k \le 9, \; 21 \le k$が棄却域であることがわかる。

表が出た回数11は、9より大きい（上図の赤で示した棄却域の内側にある）ので、有意な偏りとは言えない。 すなわち、帰無仮説『このコインの裏表が出る確率は等しい』は棄却されない。 また、計算してみると、このデータのp値は 0.200 である。

結果の解釈と検定力

もし、p値が非常に小さければ（例えば0.00001等）、帰無仮説は明らかにデータの説明に失敗しているのだから、それを棄却するのは自然である。

ところが、上記のように「中途半端」なp値の場合は、結果に対していくつかの解釈が可能となる。

仮に、p値が有意水準よりも小さな値となった場合でも、偶然、そのように小さな確率の事象が生じた可能性は依然として残る。 そのため、もともと間違いでは無かった帰無仮説を誤って棄却してしまう「間違い」が起こり得る（第１種の過誤）。

他方で、$p$値が有意水準より大きな場合（前節のコインの例では、コインに偏りがあって対立仮説が採択されるべき状況にもかかわらず）、 偶然に、偏りが小さく現れてしまう場合（第２種の過誤）も考えられる。

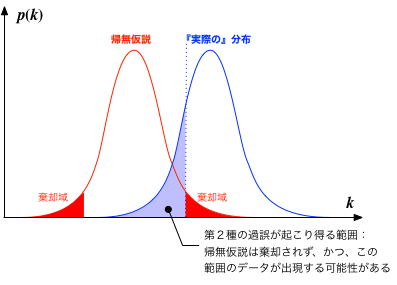
ここで、裏が出る確率が本当は $q \neq 1/2$ であったとしよう（下図の青い分布）。 帰無仮説で仮定されている分布（赤）と『実際の』分布に重なりがあると、 図で青色で塗りつぶした領域にデータが入っている場合は、帰無仮説は棄却されないことになる。 すなわち、第２種の過誤が生じる結果となってしまう。

第二種の過誤が生じる確率は、『実際の』分布を、帰無仮説の棄却域の外で積分すればよい（その確率を$\beta$とする：上図の青で塗られた面積に対応）。 $\beta$が大きければ、過誤が生じる恐れが増える。$1 - \beta$は特に検出力(power)と呼ばれる。

分布の重なり具合($\beta$)は、分布の裾野が狭いほど小さくなるので、すなわち、一般にサンプル数が大きければ$\beta$は減少し、検出力は高まる。 もし平均の差をあらかじめ見積もれるのであれば、十分な検出力を得るために必要となるサンプルの数を見積もることができる。

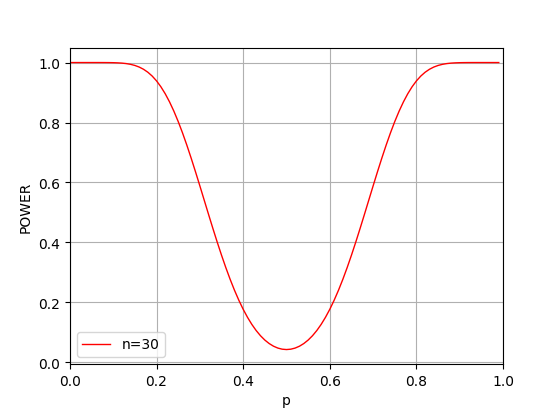
以下のコードは、サンプル数が30の場合について、『実際に』コインの表が出る確率を横軸に、その場合の検出力をプロットする例である。 教科書などでは、検定力は0.8程度以上であることが望ましいと書かれているが、プロットの結果をみると、表の出る確率が 0.25程度以下、または0.75程度以上 （相当偏ったコイン）でなければ、この検定方法では正しい判断が下し難いことが示唆される。

# coding: utf-8

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 30
alpha=0.05

kvals = np.arange(n+1)
xvals = np.arange(0,1,0.01)
power = [ ]

for x in xvals:
    beta=0
    for k in kvals:
        p1 = binom.cdf(k, n, 0.5)
        p2 = binom.cdf(k, n, 0.5) - binom.pmf(k, n, 0.5)
        if alpha/2.0<p1 and p2<1.0-alpha/2.0:
            p_alt = binom.pmf(k, n, x)
            beta += p_alt
    power.append(1.0-beta)

plt.plot(xvals,power,color=(1.0,0,0.0), linewidth=1.0, label='n='+str(n))
plt.legend()
plt.xlim(0,1)
plt.xlabel('p')
plt.ylabel('POWER')
plt.grid(True)
plt.show()

　練習：超能力の真偽

「透視能力」があるかもしれない被検者Aについて、その真偽を統計的に確かめたい。 そこで、○、☓、△　がそれぞれ書かれた３枚の紙を用意し、そのうちの１枚を内部が見えない封筒に入れた上で、中の記号を当ててもらう実験を何回か行い、その結果を統計的に分析することにした。

実験のデザインを考え、模擬的にそれを実施してみなさい。