Pythonプログラミング（ステップ７・統計計算・主成分分析）

このページでは、NumPyを使った主成分分析について考える。

多次元データの相関

$n$組のデータ$(x_i,y_i)$が与えられているとしよう。例えば、$i$番目の人の体重を$x_i$、身長を$y_i$といった具合である。 このデータの対を縦ベクトル $\boldsymbol{x}_i = \left( \begin{array}{c} x_i \\ y_i \end{array} \right)$で表し、それを連ねた行列 $$ X= \left( \begin{array}{cccc} x_1 & x_2 & \cdots & x_n \\ y_1 & y_2 & \cdots & y_n \\ \end{array} \right) $$ で表現することにする。 ここで、簡単のために、$x_i$と$y_i$の平均は0（あるいは、元のデータからそれぞれの平均を差し引いた値）であるとしよう。

これを使って、データ$X$の（分散）共分散行列$C$を $$ C \equiv \left( \begin{array}{cc} C_{xx} & C_{xy} \\ C_{yx} & C_{yy} \\ \end{array} \right) = \frac{1}{n} X X^\top $$ と表すことができる（ただし平均は0と仮定。また $X^\top$は$X$の転置）。 $C_{xx}$は$x$について、$C_{yy}$は$y$についての分散である。また明らかに$C_{xy} = C_{yx}$（共分散行列は対称行列）である。

ここで、ある行列$A$を使って、$\boldsymbol{x}_i$ を座標変換する、すなわち $$ A \boldsymbol{x}_i $$ した上で、変換後のデータの共分散行列を計算すると、「元の」共分散行列$C$を使って、 $$ \frac{1}{n} A X (A X)^\top = \frac{1}{n} A X X^\top A^\top = A C A^\top $$ と書くことができる。 ここで、$A$をうまく整えることによって、共分散行列が対角化できて、 $$ A C A^\top = \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \\ \end{array} \right) $$ となるようにしてみよう。 つまり、見方を変えることで、２つのデータの相互相関（「混じり合い」）を消すことができないか、を考えるわけである。

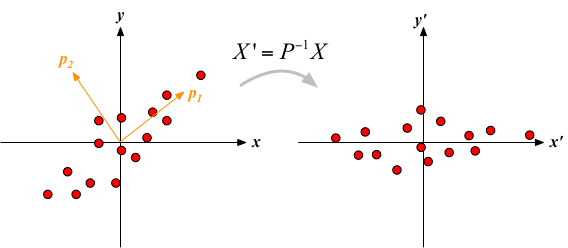
ここで$C$は対称行列であるから、固有値は全て実数で、直交行列$P$を使って $$ P^{-1} C P = \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \\ \end{array} \right) $$ と対角化できる（線形代数の教科書を参照）。すなわち、変換の行列は$A=P^{-1}$とすればよいことがわかった。 ここで$P$は、$C$の直交する固有ベクトル($\boldsymbol{p}_1, \boldsymbol{p}_2$)を並べてできる行列 $$ P = \left( \begin{array}{cc} \boldsymbol{p}_1 \; \boldsymbol{p}_2 \end{array} \right) $$ である。

主成分分析

前節での説明から明らかなように、共分散行列$C$の固有値は、座標変換後の、主軸に沿った分散である。 つまり、上記の操作は、データの統計的な変動を（相互相関を0にするという意味で）独立な成分にふるい分け、それぞれの分散を調べる作業に他ならない。 もし、$x_i$と$y_i$が完全に連成して変動していたら（極端な場合、$y_i = x_i$ならば）、変動している成分は実質的に１つだけであって、 その分散を与えるのが$C$の最大の固有値になる。 そして、残りの固有値（分散）は0である。

以上は二次元データの場合について述べたが、データの次元が上がって（変数の数が増えて）も全く同様の議論が可能である。 こうして、多変量の中から大きく変動しかつ相関が大きいグループを見つけ出す手法を主成分分析(principal component analysis）と呼ぶ。

現実的には、最大固有値を与える成分（第１主成分）以外の固有値も無視できない値を取る。 各成分の全体的な変動への寄与は、固有値（各成分の分散）の大小で見積もることができる。 データの次元を$N$とし、$k$番目の固有値を $\lambda_k$ とすると、全ての固有値の和との比率 $$ \frac{\lambda_k}{\sum_{j=1}^N \lambda_j} $$ は寄与率と呼ばれ、成分の「重要度」の尺度として使われる。

$\ell$番目の次元のデータが、第１主成分にどれくらい影響しているかを評価するために、両者の相関係数を求めてみよう。 $N$ 次元の $n$点のデータ $\boldsymbol{x}_i = (x_{1,i}, \ x_{2,i},\ x_{3,i},\ \cdots, x_{N,i})^\top$（ただし、$i=1, \cdots, n$) が与えられている状況を考えると、 第一主成分方向のデータ点の「座標」は、第一主成分の固有ベクトルを $\boldsymbol{p}_1$ とすれば、その方向への射影成分 $$ \frac{ \boldsymbol{x}_i \cdot \boldsymbol{p}_1} {\| \boldsymbol{p}_1 \|} $$ になる。

$\ell$番目の次元のデータ列 $\boldsymbol{x}^{\ell} = (x_{\ell,1},\ x_{\ell,2}, \cdots , x_{\ell,n} )$ と第一主成分との相関係数を求めるためには、まず、 $$ S = \frac{1}{n} \sum_{i=1}^n x_{\ell, i} \frac{ \boldsymbol{x}_i \cdot \boldsymbol{p}_1} {\| \boldsymbol{p}_1 \|} = \frac{1}{n} \frac{ \boldsymbol{x}^{\ell} X^\top \boldsymbol{p}_1 }{ \| \boldsymbol{p}_1 \| } $$ を計算する必要がある。 ここで、$\boldsymbol{x}^{\ell} X^\top$は、共分散行列の$\ell$行目の行ベクトルに他ならないから、固有値と固有ベクトルの関係から $$ C^{\ell} \boldsymbol{p}_1 = \lambda_1 p_{\ell} $$ すなわち、 $$ S = \frac{\lambda_1 p_{\ell}}{\| \boldsymbol{p}_1 \|} $$ となる（$p_{\ell}$は固有ベクトル$\boldsymbol{p}_1$の$\ell$番目の成分）。

次いで、規格化のために $$ Q = \frac{1}{n} \sum_{i=1}^n (x_{\ell, i})^2 = C_{\ell \ell} $$ $$ R = \frac{1}{n} \sum_{i=1}^n \left( \frac{ \boldsymbol{x}_i \cdot \boldsymbol{p}_1} {\| \boldsymbol{p}_1 \|} \right)^2 = \lambda_1 $$ と置くと、求めたい相関係数は $$ c_\ell = \frac{S}{Q^{1/2} R^{1/2}} = \frac{\sqrt{\lambda_1} p_{\ell}}{C_{\ell \ell}^{1/2} \| \boldsymbol{p}_1 \|} $$ となる。 この量は負荷（loading）と呼ばれ、第2主成分以下に対しても、同様に定義できる。

ここまでをまとると、以下の手順で主成分分析を行うことができる：

1. $N$次元のデータ$(x_{1,i}, \ x_{2,i},\ x_{3,i},\ \cdots, x_{N,i})$を$n$点サンプルする（$i=1,2,\cdots,n$)。
2. 各座標軸毎にデータの平均を計算し、元のデータから差し引いて、平均0のデータセット$X$を生成する 加えて、各変量の標準偏差が１になるように規格化しておくのが一般的な前処理の方法である（データの標準化）。
3. $C = \frac{1}{n} X X^\top$ により共分散行列を求める。
4. $C$の固有値と固有ベクトルを計算し、固有値が大きい順に並べ替える。
5. 上記に従って各成分の寄与率を計算する。
6. 上記に従って各成分の負荷を計算する。

NumPyによるコーディング

上で述べた手順に従って、Pythonによって主成分分析を行ってみよう。

サンプルとして用意したのは、プロ野球データFreakに掲載されていた、ある球団の選手全員の 身長(cm)、体重(kg)、年齢(歳)、在籍年数(年)、年俸(万円)のデータで、こちらからダウンロードできる。

ファイルからのデータの読み込み、固有値・固有ベクトル等の行列演算までコーディングするのは大変なので、ここでは、 広く使われているNumPy（ナンパイ）というライブラリを活用することにする。以下は、NumPyを使ったコードの例である：

# coding: utf-8

import numpy as np

data = np.loadtxt("rakuten-2018.txt", delimiter=" ", skiprows=1, usecols=(0,1,2,3,4) )
ndata = data.shape[0]

data[:,4] = np.log10(data[:,4])

mean = np.mean(data,0)
stdev = np.std(data,0)

for i in range(5):
    data[:,i] = (data[:,i]-mean[i])/stdev[i]

C = (data.T).dot(data) / ndata

lmda,P = np.linalg.eig(C)

print(lmda)

print("Contribution:")
for k in range(5):
    print(k,lmda[k]/np.sum(lmda))

for k in range(5):
    print("Loadings for component",k)
    p2 = np.sum( P[:,k]**2 )
    for ell in range(5):
        loading = np.sqrt(lmda[k])*P[ell,k] / ( np.sqrt(C[ell,ell] * p2 ) )
        print(ell,loading)

以下にコードの内容を補足説明する

import numpy as np

NumPyのライブラリを使えるようにする。NumPyの機能は np.何々という名前で呼び出せるようになる。

data = np.loadtxt("rakuten-2018.txt", delimiter=" ", skiprows=1, usecols=(0,1,2,3,4) )

"rakuten-2018.txt"というファイルの内容を配列データとして data にセットする。 データの各項目の区切りはスペース文字（delimiter=" "）、最初の1行はコメントなのでスキップし（skiprows=1）、 0から4列目まで（usecols=(0,1,2,3,4)）を読み込む。

ndata = data.shape[0]

行数を ndata にセットする。data.shapeは、dataの行数と列数のタプル。その0番目の要素が行数。

data[:,4] = np.log10(data[:,4])

NumPyでは、行列の要素を 行列の名前[行番号, 列番号] のように指定する。 第4列の要素それぞれに常用対数（np.log( )）を作用させ、その結果を第4列目にセットしなおす。 年俸額（万円）は選手毎に桁が違うので、その対数を分析の対象とすることにした。

mean = np.mean(data,0)
stdev = np.std(data,0)

配列dataの各列について（0は「行の方向に」を表す)、データの平均を計算し、meanにセットする。 meanには各列の平均が配列として格納されている。 同様にstdevに標準偏差をセットする。

data[:,i] = (data[:,i]-mean[i])/stdev[i]

i列目の各要素から、平均を差し引いて、各要素を標準偏差で規格化する。data[:,i]は、i列目の「最初の行から最後の行まで」を表す。

C = (data.T).dot(data) / ndata

データが格納された配列を$X$とすると、$C= X^\top X$ を計算。このページの最初の説明とは、データの配列の行と列の順が入れ替わっている点に注意。 さらに、それぞれの要素を ndata で割る。この例のように、行列に数値を演算したり、NumPyの関数を作用させると、要素毎にそれが適用される。

lmda,P = np.linalg.eig(C)

共分散行列 $C$ の固有値と固有ベクトルを計算し、それぞれ lmdaとPにセットする。

　練習：選手のデータの分析

上記のコードの内容を実行して、得られた出力に解釈を与えなさい。

　解説:NumPyのスライシング

上の主成分分析のコードでは、data[:,4]などのように、配列の添字の指定の中に : を含む箇所があった。 NumPyには添字を範囲で指定する機能があり、スライシング（slicing）と呼ぶ。その基本形は、開始位置:終了位置:ステップ である。 ステップは省略できて、開始位置:終了位置 と書くとステップが1と解釈される。 以下に、いくつか例を挙げる：

A = B[1:9:2]

A = B[:3]

A = B[3:]

Y = X[:,2]

Y = X[2:4,1:3]

口コミの分析

情報基礎A/Bの演習用に、旅行サイトが収集した宿泊施設の評価に関するアンケートデータが提供されている。 データは、宿泊施設の「立地」, 「部屋」, 「食事」, 「風呂」, 「サービス」, 「設備」, そして「総合」について、 1から5までの5段階で客ごとに尋ねた結果をCSVファイル(travel_data.csv)にまとめたもので、 「情報とデータの基礎」教材(東北大学内限定)からダウンロードできる。

このデータを読み込んで、[立地, 部屋, 食事, 風呂, サービス, 設備] の６次元の変量の配列をXにセットし、 Scikit-learnのPCAモジュールを使って主成分分析を行ってみた例を以下に示す。

# coding: utf-8

import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

data = pd.read_csv('./travel_data.csv')
print(data.dtypes)
# 0:施設ID, 1:立地, 2:部屋, 3:食事, 4:風呂, 5:サービス, 6:設備, 7:総合
X = np.array(data.values.tolist())[:,[1,2,3,4,5,6]]
N = X.shape[0]
M = 6
Z = np.array(data.values.tolist())[:,7]

mean = np.mean(X,0)
stdev = np.std(X,0)
for i in range(M):
    X[:,i] = (X[:,i]-mean[i])/stdev[i]

n_component=2
pca = PCA(n_component)
Y = pca.fit_transform(X)

lmda = pca.explained_variance_
print("Eigenvalues:")
print(lmda)

P = pca.components_
for k in range(n_component):
    print("Loadings for component",k)
    p2 = np.sum( P[k,:]**2 )
    for ell in range(M):
        loading = np.sqrt(lmda[k])*P[k,ell] / np.sqrt(p2)
        print(ell,abs(loading))

plt.scatter(Y[:,0], Y[:,1], marker='.', c=Z)
plt.xlabel('COMPONENT 1')
plt.ylabel('COMPONENT 2')
plt.colorbar()
plt.show()

ここでは、成分数を2とし、主軸が張る平面上にデータを射影してプロットしてみた。 色は「総合評価」に対応している。

第一主成分（横軸）の因子負荷量は、それぞれ

立地(0) 0.23536276575988066
部屋(1) 0.4988847102892133
食事(2) 0.4621571347461268
風呂(3)  0.4412321437208314
サービス(4) 0.4898802473541593
設備(5) 0.533792056856283

であり、設備、部屋、サービスの順に総合評価への「寄与」が大きい。 また、第二主成分については

立地(0) 0.0318203144057574
部屋(1) 0.04250971195738439
食事(2) 0.4151497107781717
風呂(3) 0.24305048941556845
サービス(4) 0.13476746062888328
設備(5) 0.25651281132360404

であり、「食事」によって（他の項目の評価に依らず）総合的な満足感が高められる可能性が示唆される。