Pythonプログラミング(ステップ7・統計計算・情報量と情報エントロピー)
このページでは、「情報」の量的表現である情報量とエントロピーについて考える。
情報のデータ化とデータの情報化
世の中にはいろいろなサービスがあって、それらの口コミ情報が溢れ、多くの場合、評価が「星」の個数などのかたちで点数化されている。 そして我々は、その点数を見ながら、どの店を選ぶか、思案したりするわけである。
サービスの質を点数化する行為について改めて考えてみよう。**ログや、**.com が得たい情報は、それぞれの店やサービス、商品の「質」や「満足度」で、色々な価値の尺度があり得る。 そして、価値に関わるような事項は、数値化が難しいはずだ。 そこで、質問項目を工夫することで、価値の方向性(評価軸)を明確化して、5段階などの尺度として回答させ、データを得ている。
情報機器を使って我々が操作できるのは、基本的に数値や記号のみである。 他方で、情報とは何らかの意味で価値と不可分であって、客観的でなかったり、表現が困難な場合も多い。 アンケート調査は、この典型的な例と言えよう。
それとは反対に、社会活動の中では、特定の目的や意図なしに、自動的に収集されているデータも膨大に存在する。 パソコンやスマートフォンを利用していると、あらゆるサービスで、アクセスや利用の状況が記録されているし、 携帯基地局やWi-Fiのアクセスポイントとモバイルデバイスがデータをやり取りする過程で、通信事業者は利用者の位置情報を把握している。 検索サービスの利用状況は、利用端末と共に、全て記録されている。 これらのデータの意味や価値は、サービスの運用が開始された当初は必ずしも明確ではなかったかもしれないが、 ビジネスの展開や社会の変化の中で、新しい使い道が見いだされてきた。 つまり、データの中から新しい情報が発掘されるような状況に至っているのが現代の社会である。
たとえば、COVID-19の流行においては、スマートフォンのロケーションデータが濃厚接触の検出に使われるようになっているが、 ウィルス感染症の拡大防止は、社会的にも、個人にとっても、有益であるとの価値判断の下に、 そのデータに新たな意味が付与されるようになったわけである。
データの尺度
着目する調査対象についての情報をデータとして表現する際に、何らかのものさし(尺度)を導入する必要がある。 統計学では、以下の分類がよく使われる:
- 名義尺度 (nominal scale)
- データをカテゴリを表す数値や記号。性別(男,女)、検査結果(陰性、陽性)など。
- 順序尺度(ordinal scale)
- データの順序・順位。成績の順位:1,2,3,...、嗜好の程度: 嫌い,やや嫌い,どちらでもない, やや好き, 好き など。
- 間隔尺度(interval scale)
- データの絶対値そのものではなく、データ間の差に意味がある尺度。摂氏や華氏の温度、試験の点数 など。
- 比例尺度(ratio scale)
- 基準値を単位とした大きさの尺度。絶対温度(ケルビン)、ほとんどの物理量。
情報量とエントロピー
自然対数を$\log$で表すと $$ \log_2(x) = \log(x) / \log(2) $$
アンケートの例に戻ると、あるサービスについての5段階評価から、我々はどれくらいの情報を得ることができるのだろうか。 その量的尺度が情報量である。 例えば、沢山のアンケートを実施して、評価 5 の割合(確率)が $P_5$ であったとすると、その情報量は $$ I = - \log_2 P_5 \;\; \textrm{[bit]} $$ となる。 対数の底を2に取った場合、その単位はビット(bit)である。 例えば、評価5が100回に1回しか得られないとすると $ I = - \log_2 (1/100) \approx 6.64 $ [bit] である。 つまり、まれにしか起きない事象に対する情報量は大きく、当たり前(確率が1に近い)の事象の情報量は 0 に近づく。 情報量は、得た情報の意外性の量的な尺度、と言える。
「良い」「悪い」など、2択の質問に対して50%ずつの割合で回答があった場合、その情報量は、 $$ - \log_2(0.5) = 1 \; \textrm{[bit]} $$ ということにある。8通りの選択肢が等しい確率で生じる場合は $$ - \log_2(2^{-8}) = 8 \; \textrm{[bit]} = 1 \; \textrm{[byte]} $$ である。このバイト(byte)は記憶装置等の容量の単位としてもよく使われる。 例えば「容量1テラバイト」というのは、1テラ = $10^{12}$ バイト = $8 \times 10^{12}$ ビットの情報量のデータを保存できる容量、ということになる。 同じことではあるが、$1 / 2^{8 \times 10^{12}}$の等しい確率で生じるような $2^{8 \times 10^{12}}$通りの事象を区別して記憶できる能力、と言ってもよい。
次に、5段階評価のアンケートのそれぞれの回答結果の割合(確率)が $\{P_1, P_2, P_3, P_4, P_5 \}$ であったとしよう。 その時、情報量の平均 $$ H = - P_1 \log_2 P_1 - P_2 \log_2 P_2 - P_3 \log_2 P_3 - P_4 \log_2 P_4 - P_5 \log_2 P_5 $$ をエントロピー(あるいは情報エントロピー、シャノンのエントロピー)と呼ぶ。 この定義は、以下のように、離散的な事象の数($N$)がいくつの場合に対しても一般化できる。 $$ H = - \sum_i^N P_i \, \log_2 P_i \;\; \textrm{[bit]} $$ エントロピーが最大になるのは、全ての回答が等しい確率の場合 ($P_i = 1/N$)で、最小となるのは、一つの回答のみ確率1で他は全て0の場合である。
連続的な確率密度 $p(x)$ に対する同様の量として、微分エントロピー $$ H = - \int p(x) \, \log p(x) \, dx $$ が使われる。 離散事象に対するエントロピーは必ず0か正値を取るのに対して、微分エントロピーは負値も取り得るなど、性質の異なる点もある。
アンケートで「たくさんの」情報を得ようとした場合、結果はできるだけ回答ごとにバラけていたほうが良いだろう。 すると、エントロピーの大きさが、得た情報の目安のひとつとして使えるはずである。 サービスの満足度について1万件の回答のうち、(悪い、やや悪い、ふつう、やや良い、良い)がそれぞれ (231, 1298, 3981, 2765, 1725) 件だったとすると、そのエントロピーは $$ \begin{eqnarray} H = - \frac{231}{10000} \log_2 \left(\frac{231}{10000}\right) - \frac{1298}{10000} \log_2 \left(\frac{1298}{10000}\right) - \frac{3981}{10000} \log_2 \left(\frac{3981}{10000}\right)\\ - \frac{2765}{10000} \log_2 \left(\frac{2765}{10000}\right) - \frac{1725}{10000} \log_2 \left(\frac{1725}{10000}\right) \approx 1.98 \; \textrm{[bit]} \end{eqnarray} $$ となる。 この場合、質問を工夫すれば4つの選択肢 ($2^2$通り)であっても、同じ量の情報が得られたかもしれないが、あくまで計算上のはなしで、 選択項目や項目数は様々なねらいのもので設定される。 例えば、実際のアンケート調査では、5件、7件、あるいは9件のように、ちょうど「中央」を設ける場合が多い。
†データの取り扱いについては、ウェブサイトの注意事項をよく読むこと。
情報とデータの基礎の演習用に提供されている、旅行サイトが収集した宿泊施設の評価に関するアンケートデータについて、情報エントロピーを求めるコードの例を以下に示した。 アンケートの集計データは、宿泊施設の立地, 部屋, 食事, 風呂, サービス, 設備, そして総合について、1から5までの5段階で客ごとに尋ねた結果をまとめたもので、 「情報とデータの基礎」教材(東北大学内限定)からダウンロードできる†。
「情報とデータの基礎」教材(東北大学内限定)
# coding: utf-8
import numpy as np
import math
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('travel_data.csv')
# 列番号と質問項目
# 0:施設ID, 1:立地, 2:部屋, 3:食事, 4:風呂, 5:サービス, 6:設備, 7:総合
x = data.values
N=x.shape[0]
ptab = np.zeros(shape=(7,5))
for i in range(N):
for j in range(7):
k = x[i,j+1]-1
ptab[j,k] += 1
for j in range(7):
ptab[j,:] = ptab[j,:] / np.sum(ptab[j,:])
for j in range(7):
H = 0
for i in range(5):
if ptab[j,i]>0:
H -= ptab[j,i] * math.log2(ptab[j,i])
print("回答",j+1," H=",H,"[bit]")
fig,axes=plt.subplots(ncols=7, nrows=1, figsize=(8, 4))
for i in range(7):
axes[i].hist(x[:,i+1], bins=5, density=True)
axes[i].set_xticks([1.4,2.2,3.0,3.8,4.6])
axes[i].set_xticklabels(["1","2","3","4","5"])
axes[i].set_ylim(0,1)
if i>0:
axes[i].tick_params(labelleft=False)
plt.show()
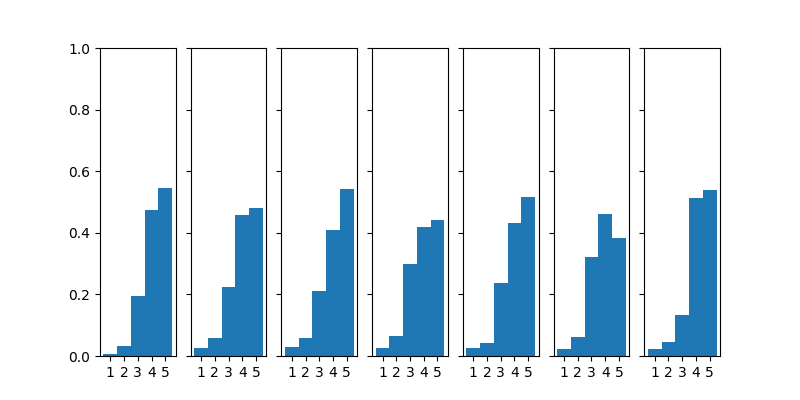
左から「立地」,「部屋」, 「食事」 「風呂」, 「サービス」, 「設備」, および「総合」の回答の分布。
 練習:アンケート結果の信憑性
練習:アンケート結果の信憑性
複数の項目について回答する際に、つい面倒に感じて、全て「5」を付けたりする場合も少なくないかもしれない。 上記のアンケートデータの中で、オール5のサンプルを除外したら、結果はどのように変わるか(変わらないか)を確認してみなさい。
相互情報量
アンケートで複数の回答項目を設けることによって、より多くの情報を得ることができそうにも思える一方で、 全ての項目が類似の点数であったとすると、項目の追加によって得られる情報量は限られるだろう。 言い換えれば、1つの項目についての情報を得たならば、他の項目についての情報も得ることができる。
XとYの2つの確率事象があった際に、『Xを知ることで、Yについて追加で得られる情報量』、あるいは『Yを知ることで、Yについて追加で得られる情報量』は相互情報量と呼ばれる。 Xが$\{x_1,x_2, \cdots, x_N\}$、Yが$\{y_1,y_2, \cdots, x_M\}$の事象で構成される場合、 それぞれの事象の確率を $p(x_i)$、$p(y_j)$、両者の結合確率を $p(x_i, y_j)$ で表すと、 $$ I(X;Y) = \sum_i^N \sum_j^M p(x_i,y_j) \log_2 \left( \frac{p(x_i,y_j)}{p(x_i) \, p(y_j)} \right) $$ で計算できる。
もしもXとYが独立、すなわち $p(x_i,y_j) = p(x_i) p(y_j)$ なら、$I(X;Y)=0$ となって、一方から他方について得られる情報が無いことに対応する。 このとき、相互情報量は最小となる。 反対に、相互情報量が大きな値であればあるほど、情報源は互いに類似していることになる。 その最も極端な場合、同じ情報源の相互情報量は、情報エントロピーに等しい: $ I(X;X) = H(X) $ 。
2つの変量の関連性の指標のひとつとして相関係数が用いられるが、相関係数はXとYの線形的な関係を想定しており、非線形な関係性の有無を検知することはできない。 一方で、相互情報量は、線型性の有無に関係無く、確率的な非独立性を検出することができる。
宿泊施設の評価アンケートの2つの項目について、相互情報量を計算するコードの例である。 このコードでは、「立地」と「総合」評価について計算する。
X = 7 Y = 1
の箇所を変更することで、他の項目同士についての相互情報量も得ることができる。
情報基礎A/B 資料(東北大学内限定)
# coding: utf-8
import numpy as np
import math
import pandas as pd
data = pd.read_csv('travel_data.csv')
# 0:施設ID, 1:立地, 2:部屋, 3:食事, 4:風呂, 5:サービス, 6:設備, 7:総合
tabs = data.values
N=tabs.shape[0]
X = 7
Y = 1
pxy = np.zeros(shape=(5,5))
px = np.zeros(shape=(5,))
py = np.zeros(shape=(5,))
for i in range(N):
x = tabs[i,X]-1
y = tabs[i,Y]-1
pxy[x,y] += 1
px[x] += 1
py[y] += 1
pxy = pxy / np.sum(pxy)
px = px / np.sum(px)
py = py / np.sum(py)
IXY=0
for x in range(5):
for y in range(5):
if px[x]>0 and py[y]>0 and pxy[x,y]>0:
IXY += pxy[x,y] * math.log2( pxy[x,y] / (px[x] * py[y]) )
print("I({0},{1})={2} [bit]".format(X,Y,IXY),sep="")
 練習:相互情報量
練習:相互情報量
質問項目の中で、「総合」評価に最も関連性の強いものはどれか、相互情報量に基づいて、分析してみなさい。