Pythonプログラミング（ステップ７・統計計算・因子分析）

このページでは、代表的な多変量解析手法のひとつである因子分析について、考え方の準備を行う。

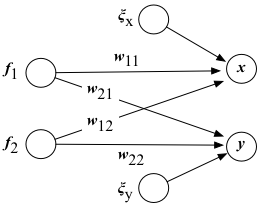
連成しながらランダムに変動する複数のデータのモデル

平均0でランダムに変動する「雑音源」$f_1$ と $f_2$ があるとしよう。それぞれの分散は1とする。 これらの雑音源からある重$w_{ij}$みで「染み出して」きた信号$x,y$を $$ \begin{eqnarray} x = w_{11} f_1 + w_{12} f_2 + \xi_x\\ y = w_{21} f_1 + w_{22} f_2 + \xi_y \end{eqnarray} $$ と表現してみよう。 ここで、混じり合いとは関係のない、固有の雑音$\xi_x, \xi_y$も存在すると仮定する（これらは平均0だが分散は任意の大きさであってよいとする）。 そしてこれらの雑音は互いに独立であると考える。

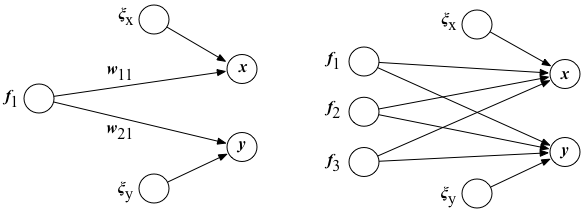
ここでは、たまたま、共通の雑音源の数と信号の数を同じとしたが、共通雑音源の数が1つの場合 $$ \begin{eqnarray} x = w_{11} f_1 + \xi_x\\ y = w_{21} f_1 + \xi_y \end{eqnarray} $$ や、逆に、共通雑音源がさらに多い場合 $$ \begin{eqnarray} x = w_{11} f_1 + w_{12} f_2 + w_{13} f_3 + \xi_x\\ y = w_{21} f_1 + w_{22} f_2 + w_{23} f_3 + \xi_y \end{eqnarray} $$ も考えられる。 一般には、共通雑音源（共通因子）の数は不明であるので、その数も含め、複数のデータの背後にある構造($w_{ij}$の値:因子負荷)を どのように推定すれば良いかを考えるのが、このページのテーマである。

連成信号の相関・共相関

この２つの信号の相関共相関行列は、平均を$E[ \cdot ]$で表し、 共通雑音を縦ベクトル $F = \left( \begin{array}{c} f_1 \\ f_2 \end{array} \right)$、 固有の雑音を対角行列 $ \Xi = \left( \begin{array}{cc} \xi_x & 0 \\ 0 & \xi_y \end{array} \right) $ と置くと、これらの行列を使って $$ \begin{eqnarray} E\left[ \left( \begin{array}{c} x \\ y \end{array} \right) (x \;\; y) \right] &=& E\left[ (W F + \Xi) (W F + \Xi)^\top \right] \\ &=& E\left[ W F F^\top W^\top + \Xi \Xi^\top + W F \Xi^\top + \Xi F W^\top \right] \\ &=& E\left[ W F F^\top W^\top \right] + E\left[ \Xi \Xi^\top \right] + E\left[ W F \Xi^\top \right] + E\left[ \Xi F W^\top \right] \end{eqnarray} $$ と書き表すことができる。

なんだかえらく複雑な式のようにも見えるが、雑音の独立性を仮定すると上の式は簡単化できる。 それぞれの雑音源（$f_1, f_2, \xi_x, \xi_y$)は互いに独立であれば、それらの相関は0、すなわち $E[ f_1 f_2 ] = E[ f_1 \xi_x ] = E[ f_1 \xi_y ] = \cdots = 0$ となる。 すると、上記の式の中で$F \Xi^\top$ や $\Xi F$ は平均すると0となる項を生成するので、結果、最後の2項は平均を取ると0行列 $$ \begin{eqnarray} E\left[ W F \Xi^\top \right] = 0 \\ E\left[ \Xi F W^\top \right] = 0 \end{eqnarray} $$ になる。また、 $$ E\left[ \Xi \Xi^\top \right] = \left( \begin{array}{cc} V_x & 0 \\ 0 & V_y \end{array} \right) $$ （ここで$V_{x}, V_{y}$は、それぞれ$\xi_x, \xi_y$の分散）である。以下ではこの対角行列を$\Psi$と表記することにする。 また、1番目の項は、$f_1, f_2$の共分散行列が、その定義より $$ E\left[ F F^\top\right] = \left( \begin{array}{cc} E[f_1 f_1] & E[f_1 f_2] \\ E[f_2 f_1] & E[f_2 f_2] \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) $$ であることに注意すると、 $$ E\left[ W F F^\top W^\top \right] = W W^\top $$ と表すことができる。

以上をまとめると、２つの信号$x, y$の分散・共分散は、行列を使って $$ W W^\top + \Psi $$ となる。

データの分散・共分散を求める

次に、データの系列 $$ X= \left( \begin{array}{cccc} x_1 & x_2 & \cdots & x_n \\ y_1 & y_2 & \cdots & y_n \\ \end{array} \right) $$ が与えられたときに、これを最もよく再現できるようなモデルのパラメータ（$W$および$\Psi$）を求める手続きについて考えてみよう。 ここでは簡単のため、各データ($\{x_i\}, \{y_i\}$の平均は0とする。 そうでないデータが与えられた場合でも、予め平均を差し引くような「前処理」を行えばよい。

与えられたサンプルの共分散は $$ C \equiv \left( \begin{array}{cc} C_{xx} & C_{xy} \\ C_{yx} & C_{yy} \end{array} \right) = \frac{1}{n} X X^\top $$ で得られるので、モデルの振る舞い方がこれになるだけ一致するようにモデルパラメータを決めればよいはずだ。 ところが、$W$ と $\Psi$ に含まれる未知数の数と$C$の要素数は一般に一致しないので、何らかの仮定や仮説が必要となる。

ガウス分布でモデル化してみる

平均0，分散1のガウス分布する独立な雑音源 $\boldsymbol{e} = (e_1 \; e_2)^\top$があったとき、それを $$ \boldsymbol{s} = \left( \begin{array}{c} s_1 \\ s_2 \end{array} \right) = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right) \left( \begin{array}{c} e_1 \\ e_2 \end{array} \right) = A \boldsymbol{e} $$ のように変換すると、$s_1, s_2$の共分散$S$は、変換行列$A$を使って $$ S = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right) \left( \begin{array}{cc} a_{11} & a_{21} \\ a_{12} & a_{22} \end{array} \right) = A A^\top $$ と書くことができる。

すると、$e_1, e_2$ の値がちょうど$(e_1, e_2)$であるような確率密度は $$ p(e_1, e_2) = \frac{1}{(\sqrt{2 \pi})^2} \exp\left(-\frac{1}{2} (e_1 \ e_2) (e_1 \ e_2)^\top \right) $$ となるが、これを$(s_1, s_2)$ に変数変換すると $$ p(s_1, s_2) = \frac{|A^{-1}|}{(\sqrt{2 \pi})^2} \exp\left(-\frac{1}{2} ( \boldsymbol{s}^\top (A^{-1})^\top A^{-1} \boldsymbol{s} ) \right) $$ ここで、逆行列の計算ルールを思い出すと $$ (A^{-1})^\top A^{-1} = (A^\top)^{-1} A^{-1} = (A A^\top)^{-1} = S^{-1} $$ なので、指数関数の中の行列の部分はスッキリと$S^{-1}$とまとめられる。 また、変換のヤコビ行列式$|A^{-1}|$は、行列式の性質から、$|A^{-1}|=1/|A|$、および$|S| = |A A^\top| = |A| |A^\top| = |A|^2$を使うと、 $1/\sqrt{|S|}$と表現できる。 以上は、変数の数がいくつでも同じことなので、$N$次元の場合、一般的に $$ p(\boldsymbol{s}) = \frac{1}{(\sqrt{2 \pi})^N \sqrt{\left| S \right|}} \exp\left(-\frac{1}{2} \boldsymbol{s}^\top S^{-1} \boldsymbol{s} \right) $$ と書くことができる。

ここで、我々が観察したデータは、多数の無相関なガウスノイズの混合によって生成されている と仮定してみよう。 我々が当初考えていたモデルの共分散、すなわち、 $$ S = W W^\top + \Psi $$ をこの仮定を当てはめると、このモデルの下で$(\textbf{x})$を観測する確率密度は $$ p(\textbf{x}) = \frac{1}{(\sqrt{2 \pi})^N \sqrt{\left| W W^\top + \Psi \right|}} \exp\left(-\frac{1}{2} \textbf{x}^\top (W W^\top + \Psi)^{-1} \textbf{x} \right) $$ となる。 ここで、対称行列$H$に対して成り立つトレース（跡）の公式 $$ \textbf{x}^\top H \textbf{x} = \textrm{tr} ( H \textbf{x} \textbf{x}^\top) $$ を使うと、 $$ p(\textbf{x}) = \frac{1}{(\sqrt{2 \pi})^N \sqrt{\left| W W^\top + \Psi \right|}} \exp\left[-\frac{1}{2} \textrm{tr} \left((W W^\top + \Psi)^{-1} \textbf{x} \textbf{x}^\top \right) \right] \tag{1} $$ と書き直せる。 これは１組のデータに対する尤度であるが、$n$組のデータについては、確率の積を考えて $$ p(X) = \frac{1}{(\sqrt{2 \pi})^{nN} \left| W W^\top + \Psi \right|^{n/2}} \exp\left[ -\frac{1}{2} \textrm{tr} \left( (W W^\top + \Psi)^{-1} X X^\top \right)　\right] \tag{2} $$ これの対数を取った量は対数尤度(log-likelihood)と呼ばれ、$C = X X^\top/n$ を思い出すと、 $$ L(C; W, \Psi) = -\frac{n N}{2} \log(2 \pi) - \frac{n}{2} \log\left| WW^\top + \Psi \right| - \frac{n}{2} \textrm{tr} \left( (W W^\top + \Psi)^{-1} C \right) $$ となる。 共分散$C$のサンプルに対する対数尤度の表式が得られたので、これを最大化するようにパラメータの組を決めればよい。

　練習：複数組のデータに対する確率分布

1回の計測でデータ$\textbf{x}$が得られる確率（式(1)）を元に、$n$回分のデータ $X = (\textbf{x}_1, \textbf{x}_2, \cdots, \textbf{x}_n)$ に対する確率が式(2)となることを示しなさい。

　ヒント

各回の計測は独立と仮定すれば、 $$ p(X) = p(\textbf{x}_1) p(\textbf{x}_2) \cdots p(\textbf{x}_n) $$ が成り立つ。