Pythonプログラミング(ステップ7・補足・二項分布)
このページでは、確率や統計の基本的事項である二項分布についてまとめておく。
1. 二項分布
表が出る確率が$p$のコイン(自動的に、裏が出る確率は$q=1-p$)を$n$回トスして、表が$k$回出る確率を考える。 それぞれのトスを独立と見なし、「表」が出る確率 $p$ の事象が $k$ 回、「裏」が出る確率 $1-p$ が $n-k$ 回が生じることと、 $n$回中、「表」が$k$回生じる場合の数が${n \choose k}$であることを考慮すると、 その確率分布は $$ f(k) = {n \choose k} p^k (1-p)^{n-k} $$ となる。これを二項分布(binomial distribution)と呼ぶ。
以下に簡単な導出方法の例を示した。
二項分布の平均は $$ n p $$ 分散は $$ n p (1-p) $$ である。
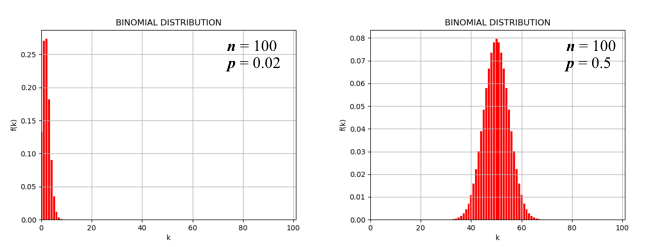
$n$が大きい場合、二項分布は2つの典型的な振る舞い方をする。 ひとつは、$p$が非常に小さい場合で、$k$が小さなところに「いびつに」偏る場合(下図左)、 他方は、$np$が$n$と比べてほどほどの大きさの場合で、平均値($np$)を中心として対称なベル型となる場合である(下図右)。 前者はポアソン分布と呼ばれる離散分布、後者は正規分布と呼ばれる連続分布でよく表現できることが知られている。
$n$が大きい場合の二項分布の典型的な形状
一般に、確率変数$X$の分布関数を$f(x)$とすると、 確率の定義より $$ \sum_x f(x) = 1 $$ 平均は $$ E(X)= \sum_x x f(x) $$
二項分布の平均と分散
まず $$ F(k,p) = \sum_{k=0}^{n} {n \choose k} p^k (1-p)^{n-k} = 1 $$ とおき、式全体を$p$で偏微分して $$ \frac{\partial F}{\partial p} = \sum_{k=0}^{n} k {n \choose k} p^{k-1} (1-p)^{n-k} - \sum_{k=0}^{n} (n-k) {n \choose k} p^{k} (1-p)^{n-k-1} = 0 \tag{1} $$ 上式の一番目の総和に$p$を乗じると、平均を$\mu$とおくと、 $$ p \sum_{k=0}^{n} k {n \choose k} p^{k-1} (1-p)^{n-k} = \sum_{k=0}^{n} k {n \choose k} p^{k} (1-p)^{n-k} = \mu $$ と書ける。同様に、二番目の総和に$1-p$を乗じると、 $$ (1-p) \sum_{k=0}^{n} (n-k) {n \choose k} p^{k} (1-p)^{n-k-1} = n - \mu $$ と書き直せるから、(1)式に$p(1-p)$を乗じて、 $$ (1-p) \mu - p n + p \mu = 0 $$ すなわち $$ \mu = n p $$ を得る。
同様に式(1)をさらに$p$で偏微分し、$\frac{\partial^2 F}{\partial p^2}=0$とおき、上の結果 $\mu=np$ と合わせて、 $$ \sum_{k=0}^{n} k^2 {n \choose k} p^k (1-p)^{n-k} = (np)^2 + np(1-p) $$ が得られる。これより、二項分布の分散(=自乗平均 - 平均の自乗)が $np(1-p)$ であることがわかった。
2. ポアソン分布
二項分布の平均を $\lambda = np$ とおいて、その値を保ったまま、$n$を大きく(同時に$p$は小さく)すると、 二項分布はポアソン分布 $$ f(k) = \frac{e^{-\lambda} \lambda^k}{k!} $$ で近似できる。 ポアソン分布の平均は $\lambda$、分散も同じく$\lambda$である。
以下は、二項分布とポアソン分布をプロットして比較するPythonコードの例である:
# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt
def binomial(k,p,n):
return math.factorial(n)/(math.factorial(k)*math.factorial(n-k)) * p**k * (1-p)**(n-k)
def poisson(k,lmda):
return lmda**k * math.exp(-lmda)/math.factorial(k)
n = int(input("n="))
p = float(input("p="))
lmda=n*p
xdata = np.arange(0,n+1,1)
N = xdata.shape[0]
binomial_data = np.empty(N)
poisson_data = np.empty(N)
for i in range(N):
k = xdata[i]
binomial_data[i] = binomial(k,p,n)
poisson_data[i] = poisson(k,lmda)
plt.title("BINOMIAL DISTRIBUTION vs POISSON DISTRIBUTION")
plt.plot(xdata,binomial_data,'.-',color=(1.0,0,0.0), linewidth=1.0)
plt.plot(xdata,poisson_data, '.-',color=(0.0,0,1.0), linewidth=1.0)
plt.xlim(0,10)
plt.xlabel('k')
plt.ylabel('p(k)')
plt.grid(True)
plt.show()
$n=100,\;p=0.02$の場合。 赤が二項分布、青がポアソン分布。
3. 正規分布
$n$が大きく、かつ $np$ も $n(1-p)$ も十分大きい場合、 二項分布を平均$\mu = np$、分散$\sigma^2 = np(1-p)$の正規分布 $$ f(k) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(k - \mu)^2}{2\sigma^2}} $$ でよく表すことができる。
以下は、二項分布と正規分布をプロットして比較するPythonコードの例である:
# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt
def binomial(k,p,n):
return math.factorial(n)/(math.factorial(k)*math.factorial(n-k)) * p**k * (1-p)**(n-k)
def normal(x,mu,sigma):
return 1/(math.sqrt(2*math.pi)*sigma) * math.exp(-(x-mu)**2/(2*sigma**2))
n = int(input("n="))
p = float(input("p="))
mu=n*p
sigma=math.sqrt(n*p*(1-p))
xdata = np.arange(0,n+1,1)
N = xdata.shape[0]
binomial_data = np.empty(N)
normal_data = np.empty(N)
for i in range(N):
k = xdata[i]
binomial_data[i] = binomial(k,p,n)
normal_data[i] = normal(k,mu,sigma)
plt.title("BINOMIAL DISTRIBUTION vs NORMAL DISTRIBUTION")
plt.plot(xdata,binomial_data,'.-',color=(1.0,0,0.0), linewidth=1.0)
plt.plot(xdata,normal_data, '.-',color=(0.0,0,1.0), linewidth=1.0)
plt.xlim(0,N)
plt.xlabel('k')
plt.ylabel('p(k)')
plt.grid(True)
plt.show()
$n=100,\;p=0.5$の場合。 赤が二項分布、青が正規分布。
 練習:負の二項分布
練習:負の二項分布
負の二項分布(negative binomial distribution)について調べ、その分布関数をPythonを使ってプロットするコードを作成してみなさい。