Pythonプログラミング（ステップ７・配列・線形代数・構造力学）

トラス構造と力の釣り合いの式

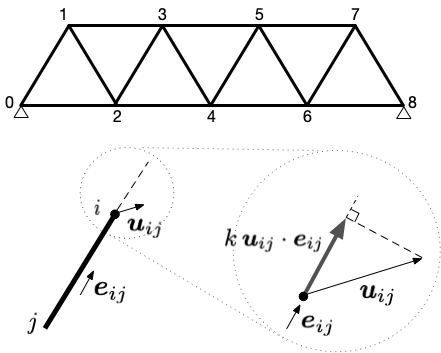
橋梁などは、トラスと呼ばれる構造で設計される場合が多い。 下図は、0と8を支点とするトラス構造の例で、「硬い」棒を太線で表しており、棒の端点は「蝶番」のように自由に回転することができる。 ここでは簡単のために棒は十分軽く質量は無視できて、たわんだりすることもないとしよう。 棒は長手方向にわずかに伸縮することができて、そのばね定数を$k$とおく。 また、棒の長さは全て等しい（簡単のため１）とする。

ここで端点$i$の釣り合いの位置からの変位をベクトル$\boldsymbol{u}_{i}$で表すことにしよう。 すると、$j$番目と$i$番目の端点を接合している棒の相対的な変形は $$ \boldsymbol{u}_{ij} = \boldsymbol{u}_{i} - \boldsymbol{u}_{j} $$ となる。 ここで、 $j$から$i$への単位ベクトルを$\boldsymbol{e}_{ij}$とおくと、変位が十分に小さければ、棒の伸び（縮み）の大きさは $ \boldsymbol{u}_{ij} \cdot \boldsymbol{e}_{ij} $ であって、それによって生じる力の大きさは（力の向きまで考慮すると） $$ {f}_{ij} = k \, \boldsymbol{u}_{ij} \cdot \boldsymbol{e}_{ij} $$ となる。 よって、それによって生じる力（ベクトル）は $$ \begin{eqnarray} \boldsymbol{f}_{ij} & = & k \, \left( \boldsymbol{u}_{ij} \cdot \boldsymbol{e}_{ij} \right) \boldsymbol{e}_{ij} \\ & = & k \, \boldsymbol{e}_{ij}^\top \boldsymbol{e}_{ij} \, \boldsymbol{u}_{ij} \end{eqnarray} $$ となる。

そうすると、端点$i$についての釣り合いは、端点$i$に作用する外力を$\boldsymbol{F}_i$とすれば、 $$ \sum_j \boldsymbol{f}_{ij} + \boldsymbol{F}_i = 0 $$ となる。

もし、棒の長さに比べて端点の変位が十分小さければ、$\boldsymbol{e}_{ij}$は一定と置いてしまっても良さそうだ（微小変形の仮定）。 すると、例えば水平から60度に立ち上がる棒については $$ \boldsymbol{e} = \begin{pmatrix} \cos(\pi/3) \\ \sin(\pi/3) \end{pmatrix} = \begin{pmatrix} 1/2 \\ \sqrt{3}/2 \end{pmatrix} $$ であるから、これから生成される行列（dyadic）は $$ A = \boldsymbol{e}^\top \boldsymbol{e} = \begin{pmatrix} 1/4 & \sqrt{3}/4 \\ \sqrt{3}/4 & 1/4 \end{pmatrix} $$ となる。 同様に、右下がり、および水平な部材については、それぞれ $$ \begin{eqnarray} B & = & \begin{pmatrix} 1/4 & - \sqrt{3}/4 \\ - \sqrt{3}/4 & 1/4 \end{pmatrix}, \\ C & = & \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}, \\ \end{eqnarray} $$ である。

改めて釣り合いの式を書き直すと $$ - \sum_j K_{ij} \, \boldsymbol{u}_{ij} = \boldsymbol{F}_i $$ となる。あるいは、全く同じことであるが $$ \sum_j K_{ij} \, \boldsymbol{u}_{ji} = \boldsymbol{F}_i $$ ここで、$K_{ij}$は、$i,j$を接合する部材の種類毎に $k \, A$, $k \, B$, および $k \, C$ のいずれかである （この$K_{ij}$は部材剛性行列と呼ばれている。ここで$k$はバネ定数）。 この式をよく眺めると、$\boldsymbol{u}_i$を未知数とする連立１次方程式となっていることが分かる。 すなわち、外力$\boldsymbol{F}_i$を与えた際の、各端点の変位を、連立方程式から求めることができる。

剛性行列の生成

ここで、$i$番目の端点のx方向の変位を$u^i_x$、y方向の変位を $u^i_y$ と表すことにして、各点の変位をベクトル $$ \boldsymbol{U} = \begin{pmatrix} u^1_x \\ u^1_y \\ u^2_x \\ u^2_y \\ \vdots \\ u^7_y \end{pmatrix} $$ で表すことにする。

それに対応して、剛性行列を $$ K = \begin{pmatrix} k_{1,1} & k_{1,2} & \cdots & k_{1,14} \\ k_{2,1} & k_{2,2} & \cdots & k_{2,14} \\ \vdots & \vdots & & \vdots \\ k_{14,1} & k_{14,2} & \cdots & k_{14,14} \end{pmatrix} $$ とおいて、釣り合いの式に対応するように、要素を設定すれば良い。

具体的には、端点$i$が$j$と連結しているときに、部材剛性行列の要素を $$ K_{ij} = \begin{pmatrix} \alpha & \beta \\ \beta & \gamma \end{pmatrix} $$ とすれば（定義から$K_{ij}$は対称）、$i$での力の釣り合の式に $$ \begin{eqnarray} \cdots - \alpha u^i_x - \beta u^i_y + \alpha u^j_x + \beta u^j_y + \cdots = F^i_x \\ \cdots - \beta u^i_x - \gamma u^i_y + \beta u^j_x + \gamma u^j_y + \cdots = F^i_y \end{eqnarray} $$ という要素が現れるので、この式の右辺をすべての連結相手の$j$について足し合わせれば（重ね合わせれば）よい。 トラス構造では、$i$は複数の端点と連結されているのが通常であるから、$u^i_x$ および $u^i_y$ の係数は、複数の部材剛性行列の要素の和となる。

変位と同様に、各接点に作用する外力をベクトル表記 $$ \boldsymbol{F} = \begin{pmatrix} f^1_x \\ f^1_y \\ f^2_x \\ f^2_y \\ \vdots \\ f^7_y \end{pmatrix} $$ すれば、外力に対する変形は $$ K \boldsymbol{U} = \boldsymbol{F} $$ を解く問題に帰着される。

シミュレーション

以上の手順をPythonコードに翻訳してみた例を以下に示す。 3種類の部材剛性行列を配列A, B, Cで定義し、 次いで、接点の連結と対応する部材剛性行列の組を、リストtrussで与えている。 それらの情報を元に、剛性行列KMATの要素を決め、 接点4に下向きの荷重を加えた条件で、各点の変位Uを求めるという流れになっている。

# coding: utf-8

import numpy as np
import math
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

A = np.array([
    [1/4, math.sqrt(3)/4],
    [math.sqrt(3)/4, 1/4]
    ]) 

B = np.array([
    [1/4, -math.sqrt(3)/4],
    [-math.sqrt(3)/4, 1/4]
    ]) 

C = np.array([
    [1, 0],
    [0, 0]
    ])

truss = [
    [1, 0, A],    [1, 2, B],    [1, 3, C],
    [2, 0, C],    [2, 1, B],    [2, 3, A],    [2, 4, C],
    [3, 1, C],    [3, 2, A],    [3, 4, B],    [3, 5, C],
    [4, 2, C],    [4, 3, B],    [4, 5, A],    [4, 6, C],
    [5, 3, C],    [5, 4, A],    [5, 6, B],    [5, 7, C],
    [6, 4, C],    [6, 5, B],    [6, 7, A],    [6, 8, C],
    [7, 5, C],    [7, 6, A],    [7, 8, B]
]

k = 200.0
N = 7
KMAT = np.zeros(shape=(N*2, N*2))

for x in truss:
    i = x[0]-1
    j = x[1]-1
    mat = k * x[2]
    KMAT[i*2,i*2] -= mat[0,0]
    KMAT[i*2+1,i*2] -= mat[1,0]
    KMAT[i*2,i*2+1] -= mat[0,1]
    KMAT[i*2+1,i*2+1] -= mat[1,1]
    if j>=0 and j<N:
        KMAT[i*2,j*2] += mat[0,0]
        KMAT[i*2+1,j*2] += mat[1,0]
        KMAT[i*2,j*2+1] += mat[0,1]
        KMAT[i*2+1,j*2+1] += mat[1,1]        

F = np.array([
    [0],[0],  # 1
    [0],[0],  # 2
    [0],[0],  # 3
    [0],[-1], # 4
    [0],[0],  # 5    
    [0],[0],  # 6
    [0],[0],  # 7
    ])

U = np.linalg.solve(KMAT,F)

print(U)

cs = math.cos(math.pi/3)
sn = math.sin(math.pi/3)
nodes = [
    [0,0],     # 0
    [cs,sn],   # 1
    [1,0],     # 2
    [cs+1,sn], # 3
    [2,0],     # 4
    [cs+2,sn], # 5
    [3,0],     # 6
    [cs+3,sn], # 7
    [4,0]      # 8
]

lines0 = [ ]
lines1 = [ ]
for x in truss:
    i = x[0]
    j = x[1]
    x0 = nodes[i][0]
    y0 = nodes[i][1]
    x1 = nodes[j][0]
    y1 = nodes[j][1]        
    lines0.append( [(x0,y0),(x1,y1)] )
    x0 = x0 + U[(i-1)*2,0]
    y0 = y0 + U[(i-1)*2+1,0]
    if j>0 and j<=N:        
        x1 = x1 + U[(j-1)*2,0]
        y1 = y1 + U[(j-1)*2+1,0]
    lines1.append( [(x0,y0),(x1,y1)] )
    
lc0 = LineCollection(lines0, color='blue', linewidths=1)
lc1 = LineCollection(lines1, color='red', linewidths=2)

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(aspect='1')
ax.add_collection(lc0)
ax.add_collection(lc1)
ax.autoscale()
plt.show()

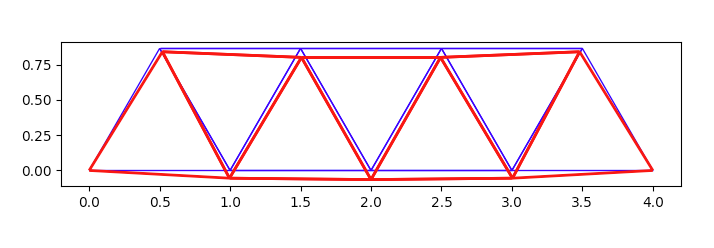
このコードを実行すると、外力が無い場合の初期位置を青、外力によって変形した状態が赤色で表示される。

　練習：構造計算

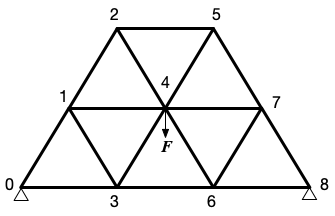
下図のようなトラス構造の場合について、同様の計算を行ってみなさい。

さらに、$K$が逆行列を持たないような場合は、どのような状況に対応するか、考えてみなさい。