Pythonプログラミング(ステップ7・配列・行列の分解・ジョルダン標準形)
このページでは、NumPyの使用例として、行列のジョルダン標準形を求めるコードを作成してみる。
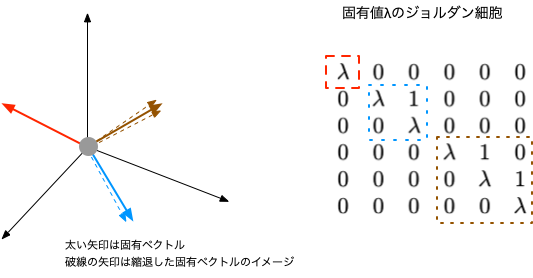
ジョルダン標準形
線形代数を学んでいくと、固有値や行列の対角化の次あたりにジョルダン標準形が登場して、 あまりにその計算が面倒なことに辟易した経験は無いだろうか(私がそうです)。 さらに、面倒な割には数値計算が不安定になりやすいこともあってか†、理論を別とすれば、実用的な計算でもお目にかかる機会がない。
ここでは、NumPyの練習問題として、University of ExeterのRobin Chapman氏のウェブサイトに掲載されているノート Computing the Jordan Canonical Form (PDF)で説明されている手順をPythonコードに「直訳」してみよう。 そのため、数値計算の効率は完全に度外視する。 背景や前提となる線形代数の知識については説明しないので、書籍やネット上の情報(例えばこちら)を参照のこと。
行列の重複した固有値(重複度6)$\lambda$のジョルダン細胞の例。 当然、空間次元は6以上になるが、それを3次元に投影したイメージ図。
固有ベクトルのいくつかが「重なって」しまうと、固有ベクトルだけでは線形独立なベクトルが足りなくなるが、 固有空間をうまい具合に拡張することで、 $P^{-1} A P$がジョルダン標準形になるような$P$を構成することができる。
計算のステップ
$n$行$n$列の行列$A$のジョルダン標準形$J$、および変換行列$P$を以下の手順で計算する($P^{-1} A P = J$)。
計算には、NumPyに加え、行列のヌル空間を求めるSciPyライブラリの関数(scipy.linalg.null_space)も用いることにする。
import numpy as np from scipy.linalg import null_space
固有値の計算
まず、numpy.linalg.eigを使って、行列$A$の固有値を全て求める。数値計算では、重複している固有値が完全に同じ値になるとは限らないので、
変数 tol 値で丸める処理を行う。
その上で、同じ固有値の数(重複度)も調べておく。
# tolerance tol = 1e-4 eigenvalues, eigenvectors = np.linalg.eig(A) rounded_eigenvalues = np.round(eigenvalues / tol) * tol unique_eigenvalues, counts = np.unique(rounded_eigenvalues, return_counts=True)
そして、それぞれの固有値$\lambda$について、反復を行いながら、ジョルダン細胞のサイズ、変換行列$P$を求めていく。
jordan_blocks=[ ]
n = A.shape[0]
P = np.empty((n,0))
for lmd,count in zip(unique_eigenvalues,counts):
.....
広義の固有空間を調べる
行列$A$の固有値$\lambda$の重複度を$r$とする。以下では$I$は単位行列を表す。
まず、固有方程式 $(A - \lambda I) \boldsymbol{v} = 0 $ の独立な解の数$r_1$を求める。 これは、行列$A - \lambda I$のヌル空間の次元に他ならないので、numpy.lialg.matrix_rank関数を使い、空間の次元から $A - \lambda I$ のランクを差し引いて求めることにする。
もし $r_1=r$ならそこまで。そうでなければ、$(A - \lambda I)^2 \boldsymbol{v} = 0$について、独立な解の数$r_2$を調べる。
もし $r_2=r$ならそこまで。そうでなければ、$(A - \lambda I)^3 \boldsymbol{v} = 0$について、独立な解の数$r_3$を求める、といった具合に、同様の操作を続ける。 そうすると、いずれ、独立な解の数が調べている固有値の重複度$r$と一致するようになる。
すなわち、$r_1 \lt r_2 \lt \cdots \lt r_N = r$となるような$N$が必ず存在し、$N$は$\lambda$についての最大のジョルダン細胞の大きさに、 $r_1$ (独立な固有ベクトルの数)はジョルダン細胞の数に、それぞれ対応する。
jordan_blocks=[ ]
n = A.shape[0]
P = np.empty((n,0))
for lmd,count in zip(unique_eigenvalues,counts):
PW = np.empty((n,0))
r = count
T = A - lmd * np.eye(n)
rs = [ ]
TN = np.copy(T)
while True:
rn = n - np.linalg.matrix_rank(TN,tol=tol) # dim of null space
rs.append(rn)
if rn==r:
break
TN = TN.dot(T)
ジョルダン細胞の大きさを決める
$s_1 = r_1, \; s_2 = r_2 - r_1, \; s_3 = r_3 - r_2, \cdots, \; s_N = r_N - r_{N-1}$のように定義すると、 $s_k$はサイズ$k \times k$以下のサイズのジョルダン細胞の総数となる。
そこで、さらに $m_1 = s_1 - s_2, \; m_2 = s_2 - s_3, \cdots, \; m_N = s_N$ を定義すると、$m_k$は固有値$\lambda$のジョルダン細胞のうち、 サイズ$k \times k$のジョルダン細胞の個数を与える。
ss = [rs[0]]
for j in range(len(rs)-1):
ss.append(rs[j+1]-rs[j])
ms = [ ]
for j in range(len(ss)-1):
ms.append(ss[j]-ss[j+1])
ms.append(ss[len(ss)-1])
ns = [ ]
for k in range(len(ms)):
if ms[k]>0:
size = k + 1
jordan_blocks.append( (lmd,size) )
ns.append(size)
これにより、リスト jordan_blocksに、ジョルダン細胞の固有値とサイズがタプルとして格納される。
変換行列を構成するベクトルを探す
上記の手順で、固有値$\lambda$に対応するジョルダン細胞の大きさが分かったら、細胞の大きさを降順に並べる: $N_1 \ge N_2 \ge \cdots \ge N_k$。
一番大きな細胞に対応する広義の固有ベクトルとして、 $(A - \lambda I)^{N_1} \boldsymbol{v}_{1,1} = 0$ を満たす非零ベクトルのうち、 $(A - \lambda I)^{N_1 - 1} \boldsymbol{v}_{1,1} \neq 0$ であるような$\boldsymbol{v}_{1,1}$を見つける。
2番目のベクトルを $\boldsymbol{v}_{1,2} = (A - \lambda I) \boldsymbol{v}_{1,1}$、 その次を $\boldsymbol{v}_{1,3} = (A - \lambda I) \boldsymbol{v}_{1,2}$ というように、 $(A - \lambda I) \boldsymbol{v}_{1,N_1} = 0$ に至るまで、芋づる式に残りのベクトルを求める。
固有値$\lambda$のジョルダン細胞が他にもある場合は、次の細胞に対応する広義の固有ベクトルとして、 $(A - \lambda I)^{N_2} \boldsymbol{v}_{1,2} = 0$ を満たす非零ベクトル$\boldsymbol{v}_{1,2}$のうち、 $(A - \lambda I)^{N_2 - 1} \boldsymbol{v}_{1,2} \neq 0$ であり、 かつ、すでに求められている固有ベクトルとも独立な $\boldsymbol{v}_{1,2}$ を見つける。
それを起点に、$\boldsymbol{v}_{2,2} = (A - \lambda I) \boldsymbol{v}_{2,1}$、 $\boldsymbol{v}_{2,3} = (A - \lambda I) \boldsymbol{v}_{2,2}$、というふうに芋づる式に残りのベクトルも求める。
同様な手続きを、細胞のサイズ$N_k$まで反復すると、$r$本の線形独立なベクトル $\boldsymbol{v}_{1,1}, \; \cdots, \boldsymbol{v}_{1,N_1}, \; \boldsymbol{v}_{2,1}, \cdots, \; \boldsymbol{v}_{k,N_k}$ が得られる。
これら用いて、固有値$\lambda$に対応する変換行列 $$ P_\lambda = \left(\boldsymbol{v}_{k,N_k}, \; \boldsymbol{v}_{k,N_k-1}, \cdots, \boldsymbol{v}_{1,1} \right) $$ が構成できる。ここで、列ベクトルの順序が反転していることに注意。
全ての固有値$\lambda$について同様の計算を行って、見つかった独立な列ベクトルを「横に」並べることで、変換行列$P$が得られる。
ns.sort(reverse=True)
for m in ns:
TM = np.linalg.matrix_power(T,m)
TM1 = np.linalg.matrix_power(T,m-1)
Z = null_space(TM)
for j in range(Z.shape[1]):
v0 = Z[:,j].reshape(-1, 1)
if np.all(np.abs(TM1.dot(v0)) > tol): # if (A - lambda E)^(m-1) neq 0
Q = np.hstack((PW,v0))
if np.linalg.matrix_rank(Q,tol=tol) > np.linalg.matrix_rank(P,tol=tol): # check v0 is independent
break
PW = np.hstack((PW,v0))
for k in range(m-1):
v0 = (T.dot(v0)).reshape(-1, 1)
PW = np.hstack((PW,v0))
PW = PW[:,::-1] # at last, reverse column order
P = np.hstack((P,PW))
ジョルダン標準形の行列を組み立てる
リスト jordan_blocksに、固有値とジョルダン細胞の大きさが格納されているので、その情報をもとに、行列全体を組み立てる。
J = np.zeros_like(A)
m=0
for lmd,size in jordan_blocks:
for i in range(m,m+size):
J[i,i] = lmd
if i+1 < m+size:
J[i,i+1] = 1
m += size
print(J)
全体のコード
以上のパーツをまとめ、上掲のウェブページの例題を実際に解かせてみた例を以下に示す:
import numpy as np
from scipy.linalg import null_space
A = np.array([[ 0, 0, 0, 0,-1,-1],
[ 0, -8, 4, -3, 1,-3],
[-3, 13, -8, 6, 2, 9],
[-2, 14, -7, 4, 2,10],
[ 1,-18, 11,-11, 2,-6],
[-1, 19,-11, 10,-2, 7]], dtype=float)
# tolerance
tol = 1e-4
eigenvalues, eigenvectors = np.linalg.eig(A)
rounded_eigenvalues = np.round(eigenvalues / tol) * tol
unique_eigenvalues, counts = np.unique(rounded_eigenvalues, return_counts=True)
jordan_blocks = [ ]
n = A.shape[0]
P = np.empty((n,0))
for lmd,count in zip(unique_eigenvalues,counts):
PW = np.empty((n,0))
r = count
T = A - lmd * np.eye(n)
rs = [ ]
TN = np.copy(T)
while True:
rn = n - np.linalg.matrix_rank(TN,tol=tol) # dim of null space
rs.append(rn)
if rn==r:
break
TN = TN.dot(T)
ss = [rs[0]]
for j in range(len(rs)-1):
ss.append(rs[j+1]-rs[j])
ms = [ ]
for j in range(len(ss)-1):
ms.append(ss[j]-ss[j+1])
ms.append(ss[len(ss)-1])
ns = [ ]
for k in range(len(ms)):
if ms[k]>0:
size = k + 1
jordan_blocks.append( (lmd,size) )
ns.append(size)
ns.sort(reverse=True)
for m in ns:
TM = np.linalg.matrix_power(T,m)
TM1 = np.linalg.matrix_power(T,m-1)
Z = null_space(TM)
for j in range(Z.shape[1]):
v0 = Z[:,j].reshape(-1, 1)
if np.all(np.abs(TM1.dot(v0)) > tol): # if (A - lambda E)^(m-1) neq 0
Q = np.hstack((PW,v0))
if np.linalg.matrix_rank(Q,tol=tol) > np.linalg.matrix_rank(P,tol=tol): # check v0 is independent
break
PW = np.hstack((PW,v0))
for k in range(m-1):
v0 = (T.dot(v0)).reshape(-1, 1)
PW = np.hstack((PW,v0))
PW = PW[:,::-1] # at last, reverse column order
P = np.hstack((P,PW))
J = np.zeros_like(A)
m=0
for lmd,size in jordan_blocks:
for i in range(m,m+size):
J[i,i] = lmd
if i+1 < m+size:
J[i,i+1] = 1
m += size
np.set_printoptions(linewidth=128)
print("J=")
print(J)
print("P=")
print(P)
print("P^-1 A P =")
Q = np.linalg.inv(P) @ A @ P
Q[np.abs(Q) < tol] = 0
print(Q)
このコードを実行すると、ジョルダン標準形 $J$、変換行列 $P$ に加え、検算として、$P^{-1} A P$が出力される。 NumPy内部の固有値計算が複素数で行われるため、出力も複素数形式の数値となっている。 固有ベクトルを選ぶ順序には任意性があるため、手計算等で求めた$P$とは異なっているかもしれないが、 検算結果は、求めたジョルダン標準形と一致していることが確認できる。
J= [[-1. 1. 0. 0. 0. 0.] [ 0. -1. 0. 0. 0. 0.] [ 0. 0. -1. 1. 0. 0.] [ 0. 0. 0. -1. 1. 0.] [ 0. 0. 0. 0. -1. 0.] [ 0. 0. 0. 0. 0. 2.]] P= [[-0.42994896+0.j 0.08923554-0.j -0.21821789+0.j -0.43643578+0.j 0. -0.j 0. -0.j] [ 0.66975567+0.j -0.56792547-0.j 0.43643578+0.j 0.21821789+0.j -0.65465367-0.j -0.19245009-0.j] [ 0.62009122+0.j -0.08006564-0.j 0.21821789+0.j 1.09108945+0.j -0.43643578-0.j 0.38490018-0.j] [-0.23980671+0.j 0.71849665-0.j -0.21821789+0.j 0.43643578+0.j 0.43643578-0.j 0.38490018-0.j] [ 0.04966445+0.j 0.18189584-0.j 0.21821789+0.j -0.43643578+0.j 0. -0.j -0.57735027-0.j] [-0.47961342+0.j 0.33728866-0.j -0.43643578+0.j 0.21821789+0.j 0.43643578-0.j 0.57735027-0.j]] P^-1 A P = [[-1.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j] [ 0.+0.j -1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j -1.+0.j 1.+0.j 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j 0.+0.j -1.+0.j 1.+0.j 0.+0.j] [ 0.+0.j 0.+0.j 0.+0.j 0.+0.j -1.+0.j 0.+0.j] [ 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 2.+0.j]]
 練習:検算
練習:検算
教科書等に掲載されている練習問題を上のコードを使って解かせてみなさい。固有値計算の丸め量(変数tol)が結果に及ぼす影響についても調べてみること。
 解説: SymPyの利用
解説: SymPyの利用
SymPyには数式処理によってジョルダン標準形を求める機能が備わっているので、特に理由がなければ、こちらを使うのが良さそうである。
import sympy as sp
A = sp.Matrix([[ 0, 0, 0, 0,-1,-1],
[ 0, -8, 4, -3, 1,-3],
[-3, 13, -8, 6, 2, 9],
[-2, 14, -7, 4, 2,10],
[ 1,-18, 11,-11, 2,-6],
[-1, 19,-11, 10,-2, 7]])
P, J = A.jordan_form()
print("J=")
sp.pprint(J)
print("P=")
sp.pprint(P)