Pythonプログラミング（ステップ７・配列・線形代数・ハウスホルダー変換）

鏡像変換（ハウスホルダー変換）

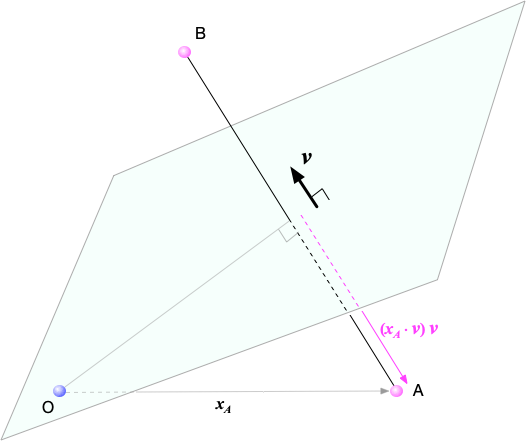
$n$次元空間の原点を通る平面を考えよう。 平面の法線ベクトルを$\boldsymbol{v} $とする。 ただし、長さは1に規格化されている$\| \boldsymbol{v} \|=1$。 この平面上の点の位置ベクトル $\boldsymbol{x} $ は法線と直交することから $$ \boldsymbol{v} \cdot \boldsymbol{x} = 0 \tag{1} $$ を満たす（平面の方程式）。

空間内の点A（$\boldsymbol{x}_A$）の、平面に対してちょうど反対側の（平面に対して鏡像関係にある）位置を点B（$\boldsymbol{x}_B$）とし、 これらの関係を考えてみよう。

$\boldsymbol{v}$が、AからBに向いているとすると、$\boldsymbol{x}_A$から平面への垂線のベクトルの長さは（向きまで考えると） $$ - \boldsymbol{x}_A \cdot \boldsymbol{v} $$ となる。 それを２倍だけ伸長すれば鏡像の点に届くわけだから $$ \boldsymbol{x}_B = \boldsymbol{x}_A - 2 (\boldsymbol{x}_A \cdot \boldsymbol{v}) \boldsymbol{v} \tag{2} $$

ここで行列$P$を $$ P = E - 2 \boldsymbol{v} \boldsymbol{v}^\top \tag{3} $$ で定義すると($E$は単位行列）、(2)式は $$ \boldsymbol{x}_B = P \, \boldsymbol{x}_A \tag{4} $$ と書き直せることがわかる。また、構成方法から $$ \boldsymbol{x}_A = P \, \boldsymbol{x}_B \tag{5} $$ も同時に成り立つことがわかる。 このことは、すなわち $$ P^2 = E \tag{6} $$ を意味する($P^{-1}=P$。$P$は直交行列)。 この鏡映変換は研究者の名前に由来して、ハウスホルダー変換と呼ばれている。

ここで、長さが$\boldsymbol{x}_A$と同じで、最初の要素のみが1、他は0であるようなベクトル $$ \boldsymbol{x}_0 = \| \boldsymbol{x}_A \| \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \tag{7} $$ を考えてみる。 そして、$\boldsymbol{x}_0$から$\boldsymbol{x}_A$の向きの単位ベクトル $$ \boldsymbol{v} = \frac{\boldsymbol{x}_A - \boldsymbol{x}_0}{\|\boldsymbol{x}_A - \boldsymbol{x}_0 \|} \tag{8} $$ を使って変換行列$P = E - 2 \boldsymbol{v} \boldsymbol{v}^\top$を構成すると、 $$ \boldsymbol{x}_0 = P \, \boldsymbol{x}_A \tag{9} $$ となる。 $\boldsymbol{x}_A$の選び方は任意であるから、このことは、任意のベクトルが第1番目の座標軸に並行とするような座標変換の構成方法を示している。

ハウスホルダー変換を用いた行列のQR分解

行列をQR分解するには、「左下」の要素が0になるようなうまい直交変換（回転、鏡映、置換）を考える必要がある。 その手続きとして、グラム・シュミットの直交化の他に、ハウスホルダー変換を用いる方法が知られている。

行列 $$ A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & & & & \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \end{pmatrix} $$ が与えられているとき、まず、その一列目に注目して、 ベクトル $$ \boldsymbol{a}_1 = \begin{pmatrix} a_{11} \\ a_{21} \\ a_{31} \\ \vdots \\ a_{n1} \\ \end{pmatrix} $$ を $$ \boldsymbol{e}_1 = \| \boldsymbol{a}_1 \| \begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} $$ への鏡像変換を構成する。

このとき、「鏡」の面を与える法線ベクトルは $$ \boldsymbol{v}_1 = \frac{\boldsymbol{a}_1 - \boldsymbol{e}_1}{\|\boldsymbol{a}_1 - \boldsymbol{e}_1 \|} $$ となるから、変換行列が $$ H_1 = E - 2 \boldsymbol{v}_1 \boldsymbol{v}_1^\top $$ で与えられる。

この変換行列を$A$に左から作用させると、$A$の第一列目は、最初の要素を除いて全て0となる： $$ \begin{pmatrix} \| \boldsymbol{a}_1 \| & a'_{12} & a'_{13} & \cdots & a'_{1n} \\ 0 & a'_{22} & a'_{23} & \cdots & a'_{2n} \\ 0 & a'_{32} & a'_{33} & \cdots & a'_{3n} \\ \vdots & & & \\ 0 & a'_{n2} & a'_{n3} &\cdots & a'_{nn} \end{pmatrix} \leftarrow H_1 \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & & & & \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \end{pmatrix} $$

続いて、変換後の行列（$H_1 A$）の1列目と1行目を除いた部分に対して、同様の鏡像変換を施す。 すなわち、ベクトル $$ \boldsymbol{a}_2 = \begin{pmatrix} a'_{22} \\ a'_{32} \\ \vdots \\ a'_{n2} \\ \end{pmatrix} $$ を $$ \boldsymbol{e}_2 = \| \boldsymbol{a}_2 \| \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} $$ に変換すべく、鏡映面の法線ベクトルを $$ \boldsymbol{v}_2 = \frac{\boldsymbol{a}_2 - \boldsymbol{e}_2}{\|\boldsymbol{a}_2 - \boldsymbol{e}_2 \|} $$ で与え、以下のように全体的な変換行列を定義する。 $$ H_2 = \left( \begin{array}{@{}c|c@{}} 1 & O \\ \hline O & E - 2 \boldsymbol{v}_2 \boldsymbol{v}_2^\top \\ \end{array} \right) $$ すると、これを使って$A$を二段階に変換すると $$ A'' \leftarrow H_2 H_1 A $$ この$A''$の１列目は2行以降が全て0、2列目は3行以降が全て0となる。

3列目に着目した鏡像変換の行列も同様に $$ H_3 = \left( \begin{array}{@{}c|c@{}} \begin{matrix} 1 & 0 \\ 0 & 1 \\ \end{matrix} & O \\ \hline O & E - 2 \boldsymbol{v}_3 \boldsymbol{v}_3^\top \\ \end{array} \right) $$ のように決めることができる。

以上のステップを繰り返すことで、 $$ R = H_{n-1} H_{n-2} \cdots H_1 A $$ のように、$A$は上三角行列$R$に最終的に変換できる。 ここで $$ H = H_{n-1} H_{n-2} \cdots H_1 $$ を定義すると、$H$は直交行列の積であるので、$H$もまた直交行列となる（ただし、一般に対称にはならない）。 そこで、$R = H A$に左から$H^\top (=H^{-1})$をかけて $$ H^\top R = A $$ となる。ここで改めて$Q = H^\top$と置き直せば、$A$のQR分解が $$ Q R = A $$ と得られる。

この一連のプロセスをNumPyを使って記述したコードの例を以下に示す：

# coding: utf-8
import numpy as np

A = np.array([
        [1,2,-3,4,5],
        [3,1,3,-1,-1],
        [-2,4,1,1,1],
        [-3,1,-3,1,2],
        [2,1,1,-3,1],
        ],dtype='float')

n = A.shape[0]
m=n
k=0
R = A[:,:]
Q = np.eye(n,dtype='float')

while m>1:
    e = np.zeros((1,m)).T
    e[0] = 1.0
    x = R[k:,k:k+1]
    nx = np.linalg.norm(x)
    e = nx * e
    v = (x-e)/np.linalg.norm(x-e)
    P = np.eye(m) - 2*v.dot(v.T)
    H = np.eye(n)
    H[k:,k:] = P[:,:]
    R = H.dot(R)
    Q = H.dot(Q)
    k=k+1
    m=m-1

Q = Q.T

print('A=\n',A)
print('Q=\n',Q)
R[R < 1.0e-15] = 0
print('R=\n',R)

固有値の計算法

行列 $A_0$が $$ A_0 = Q_0 R_0 $$ QR分解されるとき、積の順を入れ替えた行列は $$ A_1 = R_0 Q_0 = R_0 A_0 R_0^{-1} $$ となり、$A_0$と相似、すなわち同じ固有値を持つことがわかる。 同様に $A_1$の分解 $$ A_1 = Q_1 R_1 $$ から構成される行列 $$ A_2 = R_1 Q_1 = R_1 A_1 R_1^{-1} $$ もまた、$A_0, A_1$と相似になる。

$A_0$の固有値の絶対値が全て異なる場合†、 この操作を $$ \begin{eqnarray} A_k = Q_k R_k \\ A_{k+1} = R_k Q_k \end{eqnarray} $$ のように反復すると、$k$と共に$A_k$の下側の非対角要素は0に漸近し、$A_k$は右上三角行列になることが知られて（証明されて）いる。

そして、三角行列の性質から、その対角要素には固有値が並んでおり、反復の過程で行列の相似性は維持されていることから、 その固有値は出発時点の$A_0$のそれと等しい。

QR分解は一般の行列に対して可能であることから、（密な）行列の固有値を計算する際の、実用的なアルゴリズムとして知られている。