Pythonプログラミング（ステップ７・配列・線形代数・二次曲面）

球面の描画

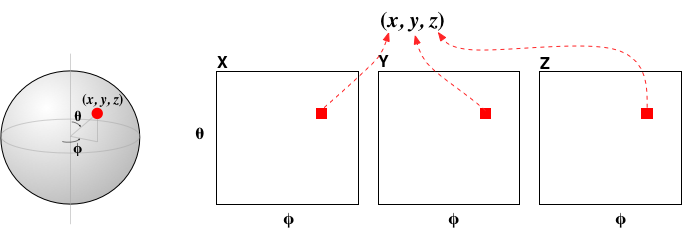
三次元座標を $(x,y,z)$ で表したとき、原点を中心とした半径 $r$ の球を表す方程式が $$ x^2 + y^2 + z^2 = r^2 \tag{1} $$ と書けることは、すでに高校までに学んだはずである。 メルカトル図法の世界地図をながめるとわかるように、球面上の点は、「北極」と「南極」を除けば、平面（矩形領域）に対応させることができる。 そこで、z軸を南北方向に取ることにして、 北極から測った角度（緯度）を$\theta$で、経度を$\phi$で表してみる（極座標）。 すると、球面上の点の座標は $$ \begin{eqnarray} x(\theta,\phi) & = & r \sin \theta \cos \phi \\ y(\theta,\phi) & = & r \sin \theta \sin \phi \\ z(\theta,\phi) & = & r \cos \theta \\ \end{eqnarray} \tag{2} $$ となる。

matplotlibライブラリのplot_surface()関数は、 このように、メルカトル図法的に座標点を与えることで、三次元内の曲面を描画することができる。

# coding: utf-8
from mpl_toolkits.mplot3d import Axes3D

import matplotlib.pyplot as plt
import numpy as np
import math

ndiv = 100
phi = np.linspace(0, 2 * math.pi, ndiv)
theta = np.linspace(0, math.pi, ndiv)

r = 1
x = np.empty((ndiv,ndiv),dtype='float32')
y = np.empty((ndiv,ndiv),dtype='float32')
z = np.empty((ndiv,ndiv),dtype='float32')

for i in range(ndiv):
    t = theta[i]
    for j in range(ndiv):
        p = phi[j]
        x[i,j] = r * math.sin(t) * math.cos(p)
        y[i,j] = r * math.sin(t) * math.sin(p)
        z[i,j] = r * math.cos(t)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, color='red', antialiased=True, shade=True)
plt.show()

二次曲面の描画

以上を踏まえて、さらに一般的に $$ a x^2 + b y^2 + c z^2 + 2 d x y + 2 e y z + 2 f z x = C \tag{3} $$ のような式で表される曲面を描く方法について考えてみよう。

上式は $$ \begin{pmatrix} x & y & z \end{pmatrix} \begin{pmatrix} a & d & e \\ d & b & f \\ e & f & c \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = C \tag{4} $$ とも書けるので、行列 $A$ を $$ A = \begin{pmatrix} a & d & e \\ d & b & f \\ e & f & c \\ \end{pmatrix} $$ ベクトル $\boldsymbol{x}$を $$ \boldsymbol{x} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$ と定義し直せば $$ \boldsymbol{x}^\top A \boldsymbol{x} = C \tag{5} $$ と、すっきりまとめることができる。

ここで、線形代数の知識を思い出すと、 $A$は対称行列であるから、対角化が可能で、固有値は全て実数である。 すなわち、対角化行列を$P$と置けば $$ P^{-1} A P = \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \\ \end{pmatrix} \tag{6} $$ とできる。 またこのとき$P$は直交行列（$P^{-1} = P^\top$）となる。 そこで、 $$ \boldsymbol{x} = P \boldsymbol{u} \tag{7} $$ のように変換した座標 $$ \boldsymbol{u} = \begin{pmatrix} u \\ v \\ w \end{pmatrix} \tag{8} $$ を用いると、 $$ \boldsymbol{x}^\top A \boldsymbol{x} = (P \boldsymbol{u})^\top A (P \boldsymbol{u}) = \boldsymbol{u}^\top P^\top A P \boldsymbol{u} = \boldsymbol{u}^\top \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \\ \end{pmatrix} \boldsymbol{u} \tag{9} $$ すなわち、 $$ \lambda_1 u^2 + \lambda_2 v^2 + \lambda_3 w^2 = C \tag{10} $$ となる。

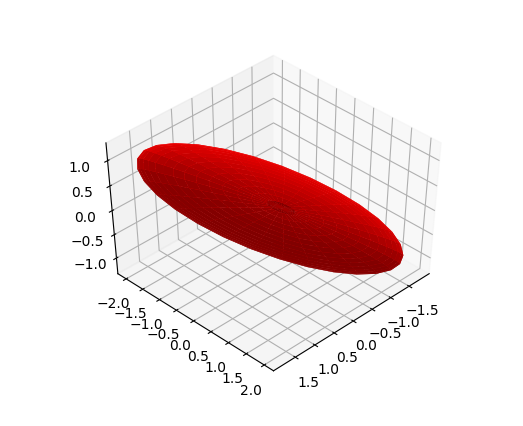
固有値が全て正の場合：楕円体の描画

固有値が全て正の場合は、 変数をスケール変換して $$ u' = \sqrt{\lambda_1} u , \;\; v' = \sqrt{\lambda_2} v , \;\; w' = \sqrt{\lambda_3} w \tag{11} $$ とすれば、 $$ {u'}^2 + {v'}^2 + {w'}^2 = C \tag{12} $$ のように、「球」に帰着できる。

以上を踏まえると、$A$の全ての固有値が正の場合の二次曲面を描画するには、以下の手順で、球の描画を少し改変すれば良い：

1. $A$の固有値と固有ベクトルを求め、$P$を得る
2. 半径$\sqrt{C}$球面の座標 $(u',v',w')$を生成する。
3. それぞれの座標軸を固有値の平方根倍だけスケールして、$\boldsymbol{u}=(u,v,w)^\top$ を得る。
4. $\boldsymbol{x} = P \boldsymbol{u}$ で得られたデータ点について（球と同様に）描画する。

# coding: utf-8
from mpl_toolkits.mplot3d import Axes3D

import matplotlib.pyplot as plt
import numpy as np
import math

ndiv = 30
phi = np.linspace(0, 2 * math.pi, ndiv)
theta = np.linspace(0, math.pi, ndiv)


u = np.empty((ndiv,ndiv),dtype='float32')
v = np.empty((ndiv,ndiv),dtype='float32')
w = np.empty((ndiv,ndiv),dtype='float32')

x = np.empty((ndiv,ndiv),dtype='float32')
y = np.empty((ndiv,ndiv),dtype='float32')
z = np.empty((ndiv,ndiv),dtype='float32')

A = np.array([
        [   1, 0.5,-0.5],
        [ 0.5, 0.7, 0.2],
        [-0.5, 0.2, 1.3]
        ], dtype='float32') 
C = 1

eig,P = np.linalg.eig(A)

print('eigen values=',eig)
print('P=\n',P)

for i in range(ndiv):
    t = theta[i]
    for j in range(ndiv):
        p = phi[j]
        u[i,j] = math.sqrt(C/eig[0]) * math.sin(t) * math.cos(p)
        v[i,j] = math.sqrt(C/eig[1]) * math.sin(t) * math.sin(p)
        w[i,j] = math.sqrt(C/eig[2]) * math.cos(t)

for i in range(ndiv):
    for j in range(ndiv):
        x[i,j] = P[0,0] * u[i,j] + P[0,1] * v[i,j] + P[0,2] * w[i,j]
        y[i,j] = P[1,0] * u[i,j] + P[1,1] * v[i,j] + P[1,2] * w[i,j]
        z[i,j] = P[2,0] * u[i,j] + P[2,1] * v[i,j] + P[2,2] * w[i,j]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=45, azim=45)
ax.plot_surface(x, y, z, color='red', antialiased=True, shade=True)
plt.show()

上のコードの出力結果の例を以下に示す。

ax.view_init(elev=45, azim=45)

の値(45)を変えることで、視点の向きを調整することができる。

双曲面の描画

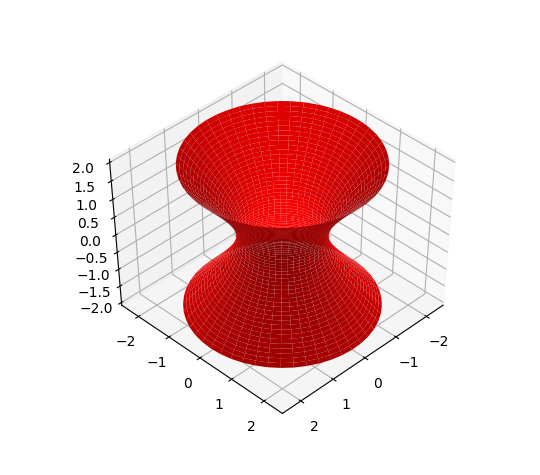
$C \gt 0$ で、固有値のうち２つが正で一つが負の場合を考える： $$ x^2 + y^2 - z^2 = C $$ この式で与えられる曲面は（一葉）双曲面と呼ばれている。

z軸に沿った「高さ」を$\xi$、「経度」を$\phi$とおいて、二次元の矩形領域と三次元座標との対応関係を $$ \begin{eqnarray} x(\xi,\phi) & = & \sqrt{C+\xi^2} \, \cos \phi \\ y(\xi,\phi) & = & \sqrt{C+\xi^2} \, \sin \phi \\ z(\xi,\phi) & = & \xi \end{eqnarray} $$ で与え、 双曲面を描画するコードの例を以下に示す：

# coding: utf-8
from mpl_toolkits.mplot3d import Axes3D

import matplotlib.pyplot as plt
import numpy as np
import math

ndiv = 50
phi = np.linspace(0, 2 * math.pi, ndiv)
xi = np.linspace(-2, 2, ndiv)

x = np.empty((ndiv,ndiv),dtype='float32')
y = np.empty((ndiv,ndiv),dtype='float32')
z = np.empty((ndiv,ndiv),dtype='float32')

C = 1

for i in range(ndiv):
    t = xi[i]
    for j in range(ndiv):
        p = phi[j]
        r = math.sqrt(C + t**2)
        x[i,j] = r * math.cos(p)
        y[i,j] = r * math.sin(p)
        z[i,j] = t

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=30, azim=45)
ax.plot_surface(x, y, z, color='red', linewidth=1, antialiased=True, shade=True)
plt.show()

　練習：二葉双曲面

$C\lt0$で、１つの固有値が負、２つが正の場合 $$ x^2 + y^2 - z^2 = C $$ について、曲面（の片側のみで良い）を描画するコードを作成してみなさい。この曲面は二葉双曲面と呼ばれている。

　発展練習：二次曲面

三次元中の二次曲面のうち、 $$ a \, x^2 + b \, y^2 + c \, z^2 + 2 d \, x y + 2 e \, y z + 2 f \, z x = C $$ で表されるものを描画する（$a,b,c,d,e,f$を入力すると、対応する図形が表示できる）Pythonコードを作成してみなさい

　ヒント