情報基礎「Pythonプログラミング」（ステップ７・配列・線形代数・画像の変形）

Pythonプログラミング（ステップ７・配列・線形代数・画像の変形）

このページでは、NumPyライブラリの線形演算機能を用いる例として、画像処理（変形）について考えてみる。

配列データとしての画像

写真などの画像をデジタルデータとして扱う場合、平面を碁盤の目のように区切り、それぞれのマス目の明るさの程度を数値化して表現する。そして、それぞれのマス目は画素、あるいは、画像（picture）の単位胞(cell)という意味を込めてピクセル（pixel）と呼ばれる。

モノクロ画像の場合は、各ピクセルには光の強度を表す数値が、カラー画像の場合は、光の三原色（赤、緑、青）それぞれの強度を表す３つの数値が割り当てられる（印刷等では、異なる色分解の方法が用いられる場合もある）。

加えて、複数の画像を重ねて合成する際に用いる情報として、「透明度」を表すアルファチャンネルが付加される場合がある。アルファ値と呼ばれる数値が０の場合は、「下地」の色がそのまま透け、反対にアルファ値が最大の場合は、そのピクセルが下地を完全に覆う。これを使って、例えば、透明な背景を持つ画像が表現できる。

ピクセルあたりの数値の数は「深さ」と呼ばれる。モノクロ画像でアルファチャネル無しの場合は深さは1、RGBカラーにアルファチャネル有りの場合は深さは4である。

光の強度、そしてアルファ値は、符号なしの８ビットの整数として表現・保存される場合が多い。人間の目は、繊細な光の強弱を区別できないことと、一般に画像は非常に多くのピクセルから構成されるので（一般的なスマートフォンのカメラでも1000万画素程度に及ぶ）画素あたりのデータ量を節約する効果も期待できる。その場合、「真っ暗」が0、最大の明るさが255に対応する。アルファ値については、完全に透明が0、完全に不透明が255である。

こうして、画素は二次元的な配列上に並ぶことになる。画像配列をDとすると

D[i, j, d]

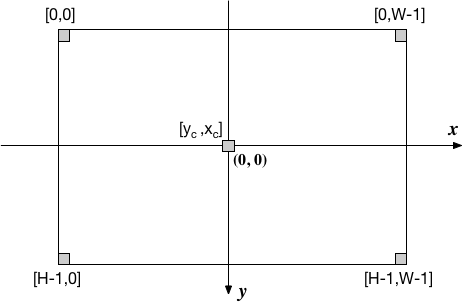
は、画像の上からi行目、左からj列目のピクセルの、深さ方向にd番目のデータを表す。つまり、左上が原点で、縦軸の向きが反転した座標系となっているので、注意が必要である。深さ4の画像の場合、$d=0$が赤、1が緑、 2が青、そして4がアルファ値にそれぞれ対応する。

以下は、画像ファイルを読み込み、NumPyの配列に変換後、それを画面表示するコードの例である。

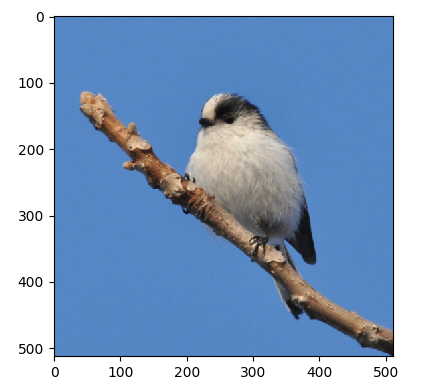
サンプル画像: bushtit.png

# coding: utf-8

import numpy as np
from skimage import io
import math

# 画像の読み込み
image = io.imread('bushtit.png')

# NumPyの配列に変換
D = np.array(image)

H = D.shape[0]
W = D.shape[1]
depth = D.shape[2]
print("幅=",W,"高さ=",H,"深さ=",depth)

io.imshow(D)
io.show()

上記のコードの出力。左上が画素座標の原点で、一般的な座標系とは、上下が反転していることに注意。

座標変換による画像の変形

$i$行$j$列目のピクセル値を $D_{ij}$ とすると、座標の原点を$(x_c, y_c)$に置いたとき。画像面内の座標 $(x,y)$との対応関係は $$ i = y + y_c, \;\; j = x + x_c $$ となる。以下では、座標の原点は、横方向の画素数を$W$ 縦を$H$とすれば、画像の中央 $$ x_c = W/2, \;\; y_c = H/2 $$ に取ることにしよう。

ここで、座標変換を表す行列 $$ A = \begin{pmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{pmatrix} $$ を与えて、$(x,y)$の画素を $$ \begin{pmatrix} u \\ v \end{pmatrix} = A \, \begin{pmatrix} x \\ y \end{pmatrix} $$ に移動する操作を全ての画素について行う。すると、行列$A$に応じて、元の画像を変形させることができる。

この考えに従って画像の変形を行うコードの例を以下に示す。

このコードでは、行列$A$の２つの固有ベクトルの方向を、赤と青の直線で、併せて表示するようになっている。

# coding: utf-8

import numpy as np
from skimage import io
from skimage.draw import line
import math

image = io.imread('bushtit.png')
D = np.array(image)

H = D.shape[0]
W = D.shape[1]
depth = D.shape[2]
T = np.zeros(shape=(H,W,depth), dtype='uint8')

# 画像の中心
xc=W/2
yc=H/2

# 変換行列
A = np.array([
        [1.1, 0.3],
        [0.7, 0.9],
        ])

# 座標変換
for j in range(W):
    for i in range(H):
        u = A[0,0]*(j-xc) + A[0,1]*(i-yc)
        v = A[1,0]*(j-xc) + A[1,1]*(i-yc)
        col = D[i,j,:]
        j2 = int(u + xc)
        i2 = int(v + yc)
        if j2>=0 and j2<W and i2>=0 and i2<H:
            T[i2,j2,:] = col[:]

# 固有値、固有ベクトル
eig,P = np.linalg.eig(A)
print('Eigenvalues=',eig)
print('Eigenvector=\n',P)

# 固有値が実数の場合、固有ベクトルの表示
if not isinstance(eig[0], complex):
    for j in range(W):
        for i in range(H):
            d0 = abs(-P[0,0] * (i-yc) + P[1,0] * (j-xc))/math.sqrt(P[0,0]**2 + P[1,0]**2) 
            d1 = abs(-P[0,1] * (i-yc) + P[1,1] * (j-xc))/math.sqrt(P[0,1]**2 + P[1,1]**2) 
            if d0<2:
                T[i,j] = [255,0,0,255]
            elif d1<2:
                T[i,j] = [0,0,255,255]

# 変換後の画像表示
io.imshow(T)
io.show()

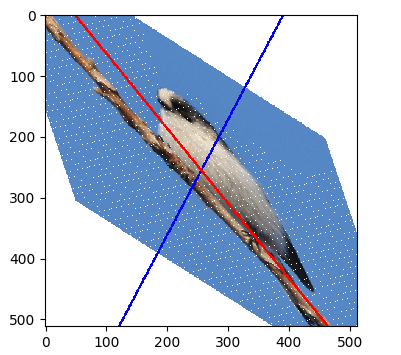
上記のコードの実行した結果の例を以下に示す。白い点は、移動先のマス目に対応する画素が無い場所に相当する。このように、離散的な位置で定義された画素を連続的に変形すると、対応する画素が欠けたり不自然なギザギザが現れたりするため、画像編集ソフト等では、周囲の画素情報を使ってデータを補う（補完する）ように工夫されている。

赤と青の線は、変換行列の固有ベクトルの方向を表す。