Pythonプログラミング（ステップ７・配列・線形代数・量子力学）

定常状態の量子状態の記述

量子力学の教えるところによれば、定常状態の波動関数を$\Psi(\boldsymbol{r})$、ハミルトニアンを$H$、エネルギーを$\epsilon$とすると、 定常状態でのシュレディンガー方程式 $$ \boldsymbol{H} \, \Psi(\boldsymbol{r}) = \epsilon \Psi(\boldsymbol{r}) \tag{1} $$ を解くことで、波動関数と系のエネルギー状態を知ることができる。

ここで、波動関数が $$ \Psi(\boldsymbol{r}) = \sum_i a_i f_i(\boldsymbol{r}) \tag{2} $$ のように互いに独立な基底関数の組 $$ \boldsymbol{f}= \begin{pmatrix} f_1(\boldsymbol{r}) \\ f_2(\boldsymbol{r})\\ \vdots \\ f_N(\boldsymbol{r}) \end{pmatrix} \tag{3} $$ を使って展開できるとする。 ただし、$f_i(\boldsymbol{r})$ の直交性はここでは仮定しない。

ここで、$f_i$の双対空間の基底を考え、$g_i$と表記することにする。 定義から両者は $$ \int f_i(\boldsymbol{r}) \, g_j(\boldsymbol{r}) \, d^3 r = \delta_{i,j} \tag{4} $$ の関係で結ばれる（$\delta_{i,j}$はクロネッカーのデルタ）。 行列 $S$ を $$ S_{ij} = \int f_i(\boldsymbol{r}) \, f^*_j(\boldsymbol{r}) \, d^3 r \tag{5} $$ で定義すると、双対基底（横ベクトル）は $$ \boldsymbol{g} = ( g_1(\boldsymbol{r}), g_2(\boldsymbol{r}), \cdots, g_N(\boldsymbol{r})) = {\boldsymbol{f}^*} \, S^{-1} \tag{6} $$ で与えられることがわかる。実際に計算してみると、 $$ \int f_i(\boldsymbol{r}) \, g_j(\boldsymbol{r}) \, d^3 r = \int f_i \, \{ \boldsymbol{f}^* \, S^{-1} \}^j \, \, d^3 r = \{S S^{-1}\}_{ij} = \delta_{i,j} \tag{7} $$ となっていることが確かめられる（ここで $\{ \cdot \}_i$ および $\{ \cdot \}^i$ はベクトルの$i$番目の要素。 $\{ \cdot \}_{ij}$は行列の$i,j$要素）。

シュレディンガー方程式(1)に左から $g_j(\boldsymbol{r})$ をかけて積分すると $$ \int d^3 r \, \left[ \sum_i S^{-1}_{ij} f^*_i(\boldsymbol{r}) \right] \boldsymbol{H} \sum_i a_i f_i(\boldsymbol{r}) = \epsilon_j \int d^3 r \, \left[ \sum_j S^{-1}_{ij} f^*_i(\boldsymbol{r}) \right] \sum_i a_i f_i(\boldsymbol{r}) \tag{8} $$

ここであらたに行列 $H$ $$ H_{ij} = \int d^3 r \; f^*_i(\boldsymbol{r}) \, \boldsymbol{H} \, f_j(\boldsymbol{r}) \tag{9} $$ と係数のベクトル $$ \boldsymbol{a} = \begin{pmatrix} a_1\\ a_2\\ \vdots\\ a_N \end{pmatrix} \tag{10} $$ を定義してまとめると $$ S^{-1} \, H \, \boldsymbol{a} = \epsilon \, \boldsymbol{a} \tag{11} $$ となる。 すなわち、行列 $S^{-1} H$の固有値が系のエネルギー、固有ベクトルが基底$\boldsymbol{f}$で波動関数を展開した場合の係数（の定数倍）を与える。 こうして、(1)式の問題を、行列の計算に帰着することができた。

しかしながら、一般に$S^{-1} H$は対称にならず、固有値計算のための効率的なアルゴリズムが使えない等の理由で、 数値計算を行う場合は$S^{-1} H$の対角化を行うのではなく、一般化固有値問題 $$ H \, \boldsymbol{a} = \epsilon \, S \, \boldsymbol{a} \tag{12} $$ の形で扱う方法が一般的である。

$S$は対称（エルミート）なのでその固有値は全て実数であり、その構成法（$i,j$要素が基底$i$と$j$の内積で与えられていること）からそれらは正値である。 すなわち、$S$を対角化するユニタリ行列を$D$、$i$番目の固有値を$\lambda_i$とすれば、 $\{ D^{-1} S D\}_{ii} = \lambda_i \gt 0$ となる。 この$D$を使って、行列 $$ A_{ij} = \frac{D_{ij}}{\sqrt{\lambda_j}} \tag{13} $$ を定義すると、 $$ A^{-1} S A = A^* S A = E \tag{14} $$ となる($E$は単位行列)。

これを使って、座標を $$ \boldsymbol{a} = A \boldsymbol{u} \tag{15} $$ のように変換すると、一般化固有方程式は $$ H A \boldsymbol{u} = \epsilon S A \boldsymbol{u} \tag{16} $$ となるが、両辺に$A^{*}$を作用させると、 $$ A^{*} H A \boldsymbol{u} = \epsilon A^{*} S A \boldsymbol{u} = \epsilon \boldsymbol{u} \tag{17} $$ を得る。ここで、$A^{*} H A$ はエルミート行列である。

以上から、エネルギー固有値と固有関数を得る手順をまとめると、

1. $S$を対角化するエルミート行列$D$を求める
2. $D$とその固有値から行列$A$を求める
3. $A^{*} H A$の固有値問題を解く
4. 得られた固有ベクトル$\boldsymbol{u}$とすると、$A \boldsymbol{u}$ で元の座標の固有ベクトルを得る

水素原子

水素原子のハミルトニアンは $$ \boldsymbol{H} = - \frac{\hbar^2}{2 m_e} \nabla^2 - \frac{q_\epsilon}{r} \tag{18} $$ で与えられる。ここで、$m_e$は換算質量、$q_\epsilon = \frac{e^2}{4\pi \epsilon_0}$, $r$は電子と原子核との相対距離である。 ボーア半径 $$ a_0 = \frac{4\pi\epsilon_0 \hbar^2}{m_e e^2} = \frac{\hbar^2}{m_e {q_\epsilon}^2} \tag{19} $$ を長さの単位として、無次元化された長さ$r' = r/a_0$ を使って方程式を書き直すと $$ \left[ -\frac{1}{2} {\nabla'}^2 - \frac{1}{r} \right] \Psi(\boldsymbol{r}') = \frac{\epsilon}{E_h} \Psi(\boldsymbol{r}') \tag{20} $$ となる、ここで、 $E_h = \frac{m_e {q_\epsilon}^2}{\hbar^2} $ （ハートリー）であり、これをエネルギーの単位に取り直すと($\epsilon = E_h \epsilon'$) 、解くべき式は、全くパラメータを持たない形 $$ \left[ -\frac{1}{2} {\nabla'}^2 - \frac{1}{r'} \right] \Psi(\boldsymbol{r}') = \epsilon' \, \Psi(\boldsymbol{r}') \tag{21} $$ になる。

教科書を開けばこの問題の厳密な解が書かれているが、仮に、それを知らなかったとすると、数値的に調べる他ない。

手始めに、「仮の」基底として球対称な関数 $$ f_i(r) = \exp(-q_i r^2) \tag{22} $$ とおいてみよう。 このとき、行列の各要素は、実際に体積積分を行うと、 $$ S_{ij} = \int \exp(-(q_i + q_j) r^2) d^3 r = 4 \pi \int_0^\infty \exp( -(q_i + q_j) r^2) r^2 dr = \left( \frac{\pi}{q_i + q_j} \right)^{3/2} \tag{23} $$ $$ H_{ij} = H^{(K)}_{ij} + H^{(V)}_{ij} \tag{24} $$ ここで、 $$ H^{(K)}_{ij} = - \frac{4\pi}{2} \int_0^\infty e^{-q_i r^2} \frac{1}{r^2} \frac{\partial }{\partial r} \left( r^2 \frac{\partial }{\partial r} e^{-q_j r^2} \right) r^2 dr \\ = \frac{1}{2} \frac{6 q_i q_j}{q_i + q_j} \left( \frac{\pi}{q_i + q_j} \right)^{3/2} \tag{25} $$ $$ H^{(V)}_{ij} = - 4\pi \int_0^\infty e^{-q_i r^2} \frac{1}{r} e^{-q_j r^2} r^2 dr = - \frac{2 \pi}{q_i + q_j} \tag{26} $$ となる。

いま、ボーア半径を長さの基準にしているので、波動関数の広がりがそのくらいのところでうまく近似できていればよいはずである。 そのようになるように、$\{q_i\}$を「適当に」選んでみる。 その上で、上記の手順に従って、エネルギー固有値・固有関数を計算しプロットするPythonコードの例を以下に示す。

# coding: utf-8

import numpy as np
import math
import matplotlib.pyplot as plt

qmin=0.0001
qmax=10
qfact=1.7
nmax=100

# 等比級数的な系列のqを生成
q = np.array([qmin*(qfact)**n for n in range(nmax) if qmin*(1.25)**n < qmax ])
N = q.shape[0]

# 行列要素の計算
S = np.zeros((N,N), dtype='float64')
H = np.zeros((N,N), dtype='float64')

for i in range(N):
    for j in range(N):
        sij = (math.pi/(q[i]+q[j]))**(3/2)
        S[i,j] = sij
        H[i,j] = 0.5*6*q[i]*q[j]/(q[i]+q[j])*sij - 2*math.pi/(q[i]+q[j])

# 固有状態の計算
lmda,D = np.linalg.eig(S)
A = D/np.sqrt(lmda[:])
B = ((A.conjugate().T).dot(H)).dot(A)
eps,U = np.linalg.eigh(B)

# 小さい固有値から順に整列
idx = eps.argsort()
eps = eps[idx]
U = U[:,idx]

# エネルギー固有値（単位：Hartree)
print(np.real(eps))

# 元の座標系に戻す
V = A.dot(U)

# 固有関数のプロット
R = np.linspace(0.0,40,200)
psi0 = np.zeros(R.shape[0])
psi1 = np.zeros(R.shape[0])
psi2 = np.zeros(R.shape[0])
psi3 = np.zeros(R.shape[0])
ps0 = 0
ps1 = 0
ps2 = 0
ps3 = 0
for i,r in enumerate(R):
    v0 = 0
    v1 = 0
    v2 = 0
    v3 = 0
    for j in range(N):
        v0 += V[j,0] * math.exp(-q[j]*r**2)
        v1 += V[j,1] * math.exp(-q[j]*r**2)
        v2 += V[j,2] * math.exp(-q[j]*r**2)
        v3 += V[j,3] * math.exp(-q[j]*r**2)
    dS = 4*math.pi*r**2
    psi0[i] = v0**2 * dS
    psi1[i] = v1**2 * dS
    psi2[i] = v2**2 * dS
    psi3[i] = v3**2 * dS
    ps0 += psi0[i]
    ps1 += psi1[i]
    ps2 += psi2[i]
    ps3 += psi3[i]

plt.title("WAVE-FUNCTION")
plt.plot(R, psi0/ps0, color=(1.0,0.0,0.0), linewidth=1.0, label="1s")
plt.plot(R, psi1/ps1, color=(0.0,1.0,0.0), linewidth=1.0, label="2s")
plt.plot(R, psi2/ps2, color=(0.0,0.0,1.0), linewidth=1.0, label="3s")
plt.plot(R, psi3/ps3, color=(0.0,1.0,1.0), linewidth=1.0, label="4s")
plt.legend()
plt.xlabel('r/a0')
plt.ylabel('PSI^2')
plt.grid(True)
plt.show()

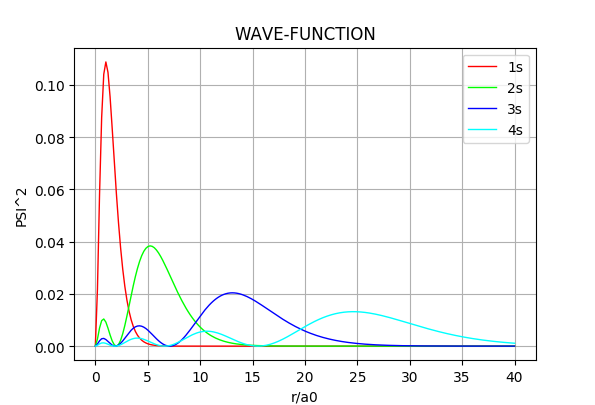
球対称な基底関数を選んでいるので、計算で求まるのはs軌道のみである。 上記のコードにより、波動関数の絶対値の２乗を、動径方向の距離の関数としてプロットした例が以下である。

　練習：計算方法の吟味

上のコードの元に、(11)式の固有値問題を解く計算も行ってみて、計算結果にどのような違いが生じるか確認してみなさい。

　発展練習：基底関数の変更

球対称ではない基底関数の例として $$ f_i(r) = z \exp(-q_i r^2) $$ で同様の計算を行うコードを作成し、結果を吟味してみなさい。

　ヒント