Pythonプログラミング（ステップ７・配列・CT）

CTを使った画像診断

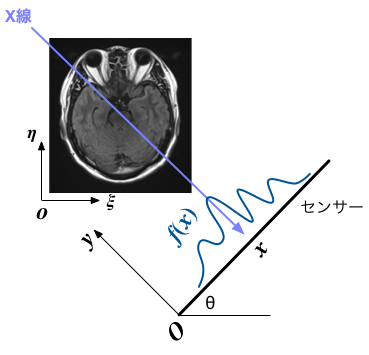
X線のように指向性と透過性の強い電磁波を物体に照射すると、内部の組成や密度に応じて吸収され、「反対側」で検出される信号の強度が変化する。 線源を並行移動しながらスキャンすることで、ある方向から見た、吸収の程度の分布を得ることができる。 センサーの方向角を $\theta$、センサー上の位置を $x$とし、その点での吸収率（信号強度から換算）を $f(\theta,x)$ と表すことにしよう。

センサーを回転させて、あるいは物体を回転させさがら、様々な$\theta$での信号強度分布 $ f(\theta,x) $ が得られたとしよう。そして、X線CT (Computed Tomography)では、まさにこうした手順で計測が行われている。

図のようなセンサーを基準にした座標上で、計測対象となる物体の位置 $(x,y)$ での電磁波の吸収率を $\rho_{\theta}(x,y)$ とすると、 センサーに到達までのあいだに、電磁波はその経路に沿って累積された分だけ減衰するので、 $x$での減衰量は $$ f(\theta,x) = \int \rho_{\theta}(x,y) \, dy \tag{1} $$ となる。そして、この$\rho_{\theta}(x,y)$が我々が知りたい（見たい）データということになる。

もしも物体内部の吸収率分布 $\rho(\xi,\eta)$がわかっていれば、 座標変換（並進と回転） $$ x = x(\xi,\eta), \, y = y(\xi, \eta) $$ から $\rho_{\theta}(x,y)$ を求めることができるので、信号強度を計算は(1)式の積分によって算出することができる。

ところが、計測可能なのは $f(\theta,x)$ のほうなのだから、こちらから $\rho(\xi,\eta)$ を何らかの方法で求めなければならない。 これはある意味で、「結果」からの「原因」の推定であって、 こうした状況設定は、一般に、逆問題（inverse problem）と呼ばれている。

CTのシミュレーション

モノクロ画像を読み込んで、その画素値を$\rho(\xi,\eta)$に見立てて、式(1)に従って減衰量を求めるPythonコードの例を以下に示す。

ここで用いる画像は $128 \times 128$ のサイズで、画像の中央を通る直線上にセンサーがあると仮定し、 角度$\theta$(°）、$x$に対応する位置（ピクセル単位）、そして式(1)で計算した「吸収量」を、リスト

[
 [角度1, 位置1, 吸収量1],
 [角度2, 位置2, 吸収量2],
 [角度3, 位置3, 吸収量3],
  ...	
]

として構成し、NumPyの配列データとしてファイルに保存する（ファイル名:scanned_data.npy)。

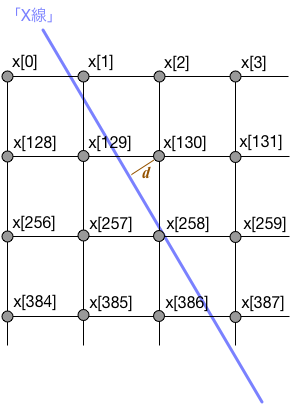
具体的には、画素値が二次元の正方格子上の点に割当られていると考え、 「X線」を想定した直線とそれら格子点との距離を求め、格子点からの距離 $d$ に応じて $$ w = \exp(-d^2/3) \tag{2} $$ の重みで信号が減衰すると仮定（あるいはモデル化）している （「X線」ビームには幅があるため。上記の関数形に特に根拠は無い）。

# coding: utf-8

import numpy as np
from PIL import Image
import math

def calc_signal(img, angle, step):
    NX = img.shape[0]
    NY = img.shape[1]
    x_c = NX/2
    y_c = NY/2
    nx = math.cos(angle*math.pi/180)
    ny = math.sin(angle*math.pi/180)
    x0 = x_c + nx * step
    y0 = y_c + ny * step
    c = -nx*x0 - ny*y0
    sig=0
    for x in range(NX):
        for y in range(NY):
            dist = abs(nx*x + ny*y + c)
            if dist<5:
                wt = math.exp(-dist*2/3.0)
                sig = sig + wt*img[x,y]
    return sig


def scan_image(img):
    data=[]
    L = int(np.max(img.shape)/2*math.sqrt(2)+1)
    for angle in np.arange(0,180,5): # step angle of 5 degrees
        print("angle=",angle)
        for step in range(-L,L,1):
            sig = calc_signal(img, angle, step)
            if sig>0:
                data.append([angle,step,sig])
    return np.array(data)

#
img = np.array(Image.open('lena.png'))

data = scan_image(img)

np.save('scanned_data.npy',data)

画像の再構成

では、前節で生成されたデータを読み込んで、画像を再構成してみよう。

もともとの画像のサイズは既知であるとして、未知である画素値を１次元配列（あるいはベクトル）として表現しておく（配列 X）。 「X線」を表す直線が与えられれば、$k$番目の格子点とその直線までの距離を $d_k$ とすると、各格子点の減衰への寄与を $w_k = \exp(-d^2/3)$とモデル化してあったのだから、減衰量の総量は $$ f(\theta,x) = \sum_k w_k X_k \tag{3} $$ と与えられる。 ここで、$f(\theta,x)$は既知であり、$w_k$も直線と格子点との位置関係から求めることができる。

$j$番目の「X線」の減衰量を $f_j$、 $k$番目の格子点の$j$本目の「X線」への寄与を $w^j_k$、 $k$番目の格子の「密度」を$X_k$とすれば、 この関係は行列を使って $$ \begin{pmatrix} w^0_0 & w^0_1 & w^0_2 & w^0_3 & \cdots & w^{0}_{M-1} \\ w^1_0 & w^1_1 & w^1_2 & w^1_3 & \cdots & w^{1}_{M-1} \\ w^2_0 & w^0_1 & w^0_2 & w^0_3 & \cdots & w^{2}_{M-1} \\ \vdots & & & & & \\ w^{N-1}_0 & w^{N-1}_1 & w^{N-1}_2 & w^{N-1}_3 & \cdots & w^{N-1}_{M-1}\\ \end{pmatrix} \begin{pmatrix} X_0 \\ X_1 \\ X_2 \\ X_3 \\ \vdots \\ X_{M-1} \\ \end{pmatrix} = \begin{pmatrix} f_0 \\ f_1 \\ f_2 \\ \vdots \\ f_{N-1} \\ \end{pmatrix} \tag{4} $$ とまとめることができる。 以下では、これを簡単に $$ W X = F \tag{5} $$ と表記することにする。 ここで、$W$の列数$M$は画像のピクセル数、行数$N$はデータの点数に等しい。

行列$W$のrankが$X$の次元（$M$）に等しくなるとは限らないから、式(5)を$X$について一意に解くことは一般にはできない。 そのため、データとの二乗偏差 $$ D = \| F - W X \|^2 = \sum_j \left( f_j - \sum_k w^j_k X_k \right)^2 \tag{6} $$ を最小とするような$X$を推定値とする方法がよく採られている（最小二乗法）。

未知数の数$N$は画素数に他ならないので、この例題の場合ですら$128^2=16384$であり、実用的な問題の$W$は一般に大規模な行列となる。 また、「X線」が通過する付近以外の格子点は吸収に寄与しないことから、$W$のほとんどの要素は0（疎行列;sparse matrix)となる。

ここでは、SciPyライブラリの中の疎行列用のソルバーである sparse.linalg.lsqr を使って、この逆問題を解かせてみよう。

以下に具体的なコードの例を示す。 前節のコードが生成したデータ（scanned_data.npy）を読み込み、 計算結果から再構成した画像をファイル（reconstructed_image.png）に出力する。 なお、大きなサイズの行列計算を伴うので、一般的なパソコンでは処理が完了するまで数分程度以上を要するので注意すること。

# coding: utf-8

import numpy as np
from scipy.sparse import lil_matrix,csc_matrix
from scipy.sparse.linalg import lsqr
from PIL import Image
import math

def gen_col_index(NX,NY,angle,step):
    L = int(max(NX,NY)*1.42)
    nx = math.cos(angle*math.pi/180)
    ny = math.sin(angle*math.pi/180)
    x0 = NX/2 + nx * step
    y0 = NY/2 + ny * step
    c = -nx*x0 - ny*y0
    cols=[ ]
    if abs(nx)>abs(ny):
        for y in range(NY):
            x1 = int(-(ny*y+c)/nx+0.5)
            for x in range(x1-5,x1+6):
                if x<0 or x>=NX:
                    continue
                dist = abs(nx*x+ny*y+c)
                if dist<5:
                    wt = math.exp(-dist**2/3.0)
                    k = x + y*NX
                    cols.append([k,wt])
    else:
        for x in range(NX):
            y1 = int(-(nx*x+c)/ny + 0.5)
            for y in range(y1-5,y1+6):
                if y<0 or y>=NY:
                    continue
                dist = abs(nx*x+ny*y+c)
                if dist<5:
                    wt = math.exp(-dist**2/3.0)
                    k = x + y*NX
                    cols.append([k,wt])
        
    return cols

def gen_matrix(NX,NY,data):
    N = data.shape[0]
    M = NX*NY
    W = lil_matrix((N,M))
    F = np.zeros((N,))
    for j,x in enumerate(data):
        angle = x[0]
        step = x[1]
        val = x[2]
        cols = gen_col_index(NX,NY,angle,step)
        for k,wt in cols:
            W[j,k]=wt
        F[j]=val
    return W,F


###
data = np.load('scanned_data.npy')
NX=128
NY=128

W,F = gen_matrix(NX,NY,data)
W = csc_matrix(W)

res = lsqr(W,F,show=True,iter_lim=100)
X = res[0]

image = np.zeros((NX,NY))
for x in range(NX):
    for y in range(NY):
        val = X[x + y*NX]
        image[x,y] = val

pil_img = Image.fromarray(image.astype(np.uint8))
pil_img.show()
pil_img.save('reconstructed_image.png')

上記のコードで再構成された画像を以下に示す。

　練習：画像を使った実験

グレースケールの小さめの画像ファイルを用意し、それを使って上記のシミュレーションを追試してみなさい。

• 上の例では、方向角を5度毎にサンプルを取得しているが、それを倍程度、あるいは半分程度にすると結果はどのように変わるか。
• それぞれの格子点の影響度を与えるモデル（式(2)）が結果にどのように影響するか。