Pythonプログラミング（ステップ６・SIRモデル・補足2）

このページでは、Pythonの学習とは関係無いが、感性症拡大の長期的な制御について、あれこれ考えてみる。

感染状況を制御する

クラシックなSIRモデルをベースに考える。 全人口に占める罹患していない人(S)の割合を $x(t)$、感染者(I)の割合を $y(t)$、回復者(R)の割合を $z(t)$ と置くと、 基本的なモデルは $$ \begin{eqnarray} \frac{d x(t)}{d t} & = & - \beta(t) \, x(t) \, y(t) \tag{1} \\ \frac{d y(t)}{d t} & = & \beta(t) \, x(t) \, y(t) - \gamma y(t) \tag{2} \\ \frac{d z(t)}{d t} & = & \gamma y(t) \tag{3} \\ \end{eqnarray} $$ となる。 ここで、感染の状況に応じて人々の接触を抑制することで、$\beta$ が調整されていることを反映し、$\beta$ も時間に依存した変数と考えた。

$\beta$ の調整メカニズムは、政治や経済の動力学に依るので数式では表しにくいものの、 「感染者の数 $y(t)$ が上昇すれば$\beta$を減らし、減少すれば制限を緩和する（$\beta$を増やす）」という原則は、どのような社会（あるいは為政者）であっても、逸脱することはないはずである。 すると、その基本的な様態は、 $$ \frac{d \beta(t)}{d t} = -\eta \frac{d y(t-T)}{d t} \tag{4} $$ で概ね表現できるのではないか†。 ここでの時間遅れ $T$ は、検査により発病日が明らかになるまでに要する時間に対応する。 また $\eta$ は感染状況に対する施策の「感度」（あるいは増幅率）に対応する定数である。

† 感染症の拡大が乗算的な過程であることを考えると、ここのところは $$ \frac{d \beta(t)}{d t} = -\eta \frac{1}{y(t-T)} \frac{d y(t-T)}{d t} $$ としたほうがより適切かもしれない。

もしも、検査が不十分で、感染者の増減の様子が正しく把握できていなければ（あるいは、状況は分かっていても、それが政策に反映されにくければ）、$\eta$は0に近くなる。 一方で、状況が正確に把握され、その都度、機敏な対応が成されれば、$\eta$の値は大きくなる。

では、この$\eta$の値は実際にはどれくらいと 見積もられるだろうか。 東京都の場合、2020年4月の前半の新型コロナウイルスの患者数は最大で200人/日程度のペースで増えていた。 人口が1000万人とすると、その頃の増加率(1/日)は $$ \frac{dy}{dt} \approx \frac{200}{10000000} = 2 \times 10^{-5} $$ （ただし、実際の罹患者数はこれよりかなり多いのではないかと言われている）。

他方で、同時期の基本再生算数が $R_0 = \frac{\beta}{\gamma} \approx 2.5$ 程度であったとし、患者の回復までの日数の逆数を $\gamma=0.1$(1/日）と仮定すると $\beta \approx 0.25$ 。 これを2週間程度で$0.1$程度まで削減しようとするのだから、 $$ \frac{d \beta}{d t} \approx - \frac{0.15}{14} = -0.01 $$ すると、$\eta$ は $$ \eta \approx \frac{10^{-2}}{2 \times 10^{-5}} = 5 \times 10^{2} $$ 程度に設定されていたと見積もれる。

数値シミュレーション

上述のモデルは非線形で、かつ時間遅れ（むだ時間）を含むので、一般的な解析は（少なくとも著者にとっては）難しい。 そこで、Pythonでその様子だけでもシミュレーションしてみよう。

以下のコードでは、初期状態での $\beta$ が0.25（1日あたりの接触回数と感染確率の積が0.25）、$\gamma$ が0.1（回復に必要な時間が約10日間）、 初期感染者が人口の0.001%であるような状況を想定している。 また、発病日は 7 日遅れて把握できるとし($T=7$)、 制御の「増幅率」は $\eta = 500$ と仮定した。

また、プロットの際、$y$と$z$は値を100倍にした。

# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt

x = 1.0-0.00001
y = 0.00001
z = 0

taxis=[ ]
xaxis=[ ]
yaxis=[ ]
zaxis=[ ]
baxis=[ ]

beta=0.25
gamma=0.1
eta = 500.0

dt=0.01
tau = 7

mtau = int(tau/dt)
ky1mem=np.zeros((mtau+1,))
ky2mem=np.zeros((mtau+1,))

t = 0
cnt=0
while t<180:
    if cnt%100==0:
        taxis.append(t)
        xaxis.append(x)
        yaxis.append(y*100)
        zaxis.append(z*100)
        baxis.append(beta)
# step 1
    kx1 = - beta*x*y
    ky1 = beta*x*y - gamma*y
    ky1mem = np.roll(ky1mem,1)
    ky1mem[0]=ky1
    kb1 = - eta*ky1mem[mtau]
# step 2
    t2 = t+dt
    x2 = x + kx1*dt
    y2 = y + ky1*dt
    b2 = beta + kb1*dt
    kx2 = - b2*x2*y2
    ky2 = b2*x2*y2 - gamma*y2
    ky2mem = np.roll(ky2mem,1)
    ky2mem[0]=ky2
    kb2 = - eta*ky2mem[mtau]
# update
    x = x + (kx1+kx2)*dt/2
    y = y + (ky1+ky2)*dt/2
    beta = beta + (kb1+kb2)*dt/2
    z = 1 - x - y
    t = t + dt
    cnt = cnt + 1

plt.title("SIRB MODEL")
plt.plot(taxis,baxis, color=(0.0,1,1.0), linewidth=1.0, label='BETA')
plt.plot(taxis,xaxis, color=(0.0,1,0.0), linewidth=1.0, label='S')
plt.plot(taxis,yaxis, color=(1.0,0,0.0), linewidth=1.0, label='I')
plt.plot(taxis,zaxis, color=(0.0,0,1.0), linewidth=1.0, label='R')
plt.xlim(0,180)
plt.ylim(0,1)
plt.legend()
plt.xlabel('DAY')
plt.ylabel('X, Y*100, Z*100, BETA')
plt.grid(True)
plt.show()

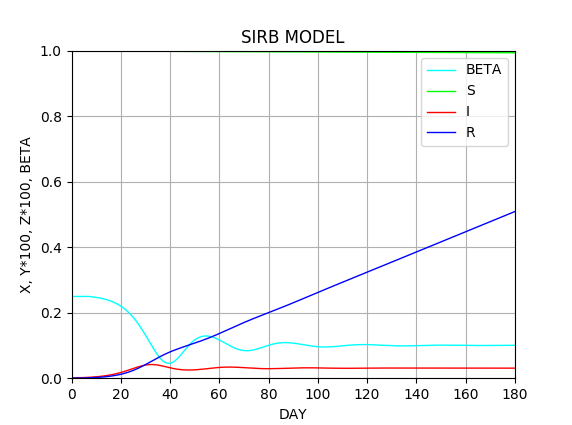
コードを実行してみると、$\beta$は徐々に下降し、患者数が一定になるようなところ（$R_0=1$が達成されるところ）で落ち着くことがわかる。 $0.25$を$0.1$まで落としたことになるので、接触を $0.1/0.25 = 0.4$ まで下げたこと(60%削減)に相当する。 そして、その後の患者数はほぼ一定のまま推移する。

多少振動的になっているのは、フィードバックに時間遅れがあるためである。 時間遅れ$T$を大きすると、$\beta$はさらに振動的になり、制御が困難になる様子が観察できる。

IとRは値を100倍した。

このシミュレーションは、ある意味で、感染爆発を抑えるための「ぎりぎりのところ」を表していると考えられる。 このおもちゃモデルから以下が示唆される：