Pythonプログラミング(ステップ1・計算機科学的な発想と問題の抽象化)
このステップの目標
- 問題の抽象化の例を通じて、計算機科学流の問題の捉え方を追体験する。
1. 総和「だけ」を得る方法
ここに挙げた例をさらにきちんと論じているのがsecure multi-party computationと呼ばれる研究分野である。
あなたはあるセミナーを主宰していて、そこには10名の参加者が居るとしよう。 セミナーは(例えば)健康に関する内容のため、参加者の平均年齢を知る必要があった。 プライバシー上の配慮から、あなたは参加者毎に年齢を尋ねることはできず、また、参加者も自分の年齢は他に知られなくない。 一人ひとりが年齢を「告白」することなく参加者全体の平均年齢を知る、うまい方法は無いだろうか?
ここで、平均年齢は全体の年齢の総和を人数で割った値だから、全体の年齢の合計値が分かれば十分である。
そのひとつの解法は以下のとおりである:
- 紙をあなたと参加者の数(11枚)だけ用意し、1枚ずつ配る
- あなたは、紙に秘密の数字(例えば752)を書き、それを頭に記憶した上で、1番目の参加者に渡す。
- 1番目の参加者は、紙に書かれた数値に、自分の年齢を加えた値を新たに紙に記入し、2番目に渡す。
- 同様の手続きを最後の参加者まで繰り返す。
- 最後の参加者が足し算を終えたら、あなたはその結果を記した紙を受け取り、その数値から記憶しておいた数値を引いた上で、値を公表する。
この方法はもちろん完全ではない。 例えば、参加者が少ない場合(極端な場合、例えば2人)、総和から自分の年齢を引けば、相手の年齢が分かってしまう。 また、誰かが嘘の申告をしても、それを知る術はない。
 練習:完全匿名投票
練習:完全匿名投票
クラスで大学祭に出展するかどうかを決めたい。 全員一致の場合のみ参加することとし、後から気まずくならないように、反対があった場合は、反対票が何名分であったかは誰にも分からないようにしたい (つまり、投票結果は、「全員イエス」か「それ以外」)。 投票の方法をデザインしなさい。
 解説: 情報の秘匿化
解説: 情報の秘匿化
年齢の総和を求める手順の例では、仮に、総年齢が判ったとしても、同じ総和を与えるような年齢の組み合わせは多数あるため、 どの組み合わせなのかは分からない、という意味で、個人情報は「安全に」守られる。 形式的には、年齢の組 $ A = \{a_1, a_2, \cdots, a_N\} $から、総和 $S$ への写像 $F: A \to S$ は一意に決まり簡単に計算できるが、 その逆($S \to A$)は簡単には求まらない、と言うこともできる。
ITの世界では、パスワード等の秘密情報も、同様の発想で管理されている。あなたが決めたパスワードの文字列を $A$ とすると、それをある(非常に大きな)数に変換 するための計算式(ハッシュ関数; $F$に対応)が考案されていて、サーバーには、その値(ハッシュ値; $S$に対応)のみが保管されている。 あなたが入力したパスワードは、その都度、計算され、それがハッシュ値と等しければ、正しいパスワードであると判る。 逆に、万一ハッシュ値が漏洩しても、そこから、元のパスワードを知ることができない。
このように、入力から出力は簡単に計算できるが、出力から入力を「計算」することが困難な関数は、一方向関数(one-way function)と呼ばれ、 計算機科学の分野で研究され、社会の各所で(人知れず)広く使われている。
上記の年齢調査の例で、主宰者が最初に記入した数値は、ハッシュ関数($F$)を調整するための補助的な変数と見做すことができる。 実際の情報セキュリティの現場でも、ハッシュ値の計算の途中にランダムな値を「混ぜて」安全性を高める工夫(「ソルト」と呼ばれる)が成されている。
なお、上記の例で、「総和」は実用的なハッシュ関数に求められる性質の一面しか備えていない。 というのは、ある $S$ を与えるような $A$ (の別の例)を容易に生成することができてしまうからだ。 パスワードの照合等に実際に使われるハッシュ関数は、仮にハッシュ値が分かったとしても、 その値が生成されるような $A$ の例を見つけることも困難なように設計されている。
 発展練習:「正直」なアンケート
発展練習:「正直」なアンケート
ある大規模な大学で、定期試験での不正行為の経験の有無について調査を行うことにした。 ただし、個人は特定せず、どのくらいの割合の学生がそのような経験を持っているのかのみを把握したい。 回答はアンケート用紙を用いて行い、記入内容が他人の目に触れる可能性もあり得ると想定する。
このような状況で、意味のあるデータを取得するための方法を考えてみなさい。
2. 階段のスイッチの動作を抽象的に考えてみる
数階建てのビルの階段を想像してみよう。それぞれの階には照明のスイッチがあって、ある階のスイッチを切り替えると階段全体の照明が灯るが、別の階をスイッチを反対側に倒すと消える。 日々の生活でよく目にする(お世話になる)この仕掛けを、少し抽象的に眺めてみよう。
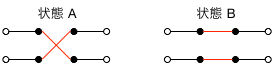
それぞれの階のスイッチには2つの状態があるので、それを $A$, $B$ と区別することにする。 つまり、各階のスイッチはこの $A$ と $B$ の状態が交互に切り替わる、と考える。 また、電灯の状態については、階段の明かりが灯っている(通電している)ときを $s_1$, 消えている場合を $s_0$ という記号で区別することにしよう。
ここで、『通電していたときに $A$ の状態のスイッチを回路に入れると、明かりが消える』、という振舞いを $$ A s_1 \to s_0 $$ と表現してみる。この式は、『$s_1$ に $A$ が作用すると$s_0$ になる』と解釈すればよい。 反対に、もともと通電していなかったときに同じ操作をすると、今度は明かりが灯ることになるのだから、 $$ A s_0 \to s_1 $$ も同時に成り立つべきである。
他方で $B$は、通電の状態を変えない。すなわち、 $$ B s_1 \to s_1 $$ および $$ B s_0 \to s_0 $$ とする。
すると、例えば、スイッチの組み合わせが、1階が $A$, 2階が $A$, 3階が $B$, 4階が $A$ であるような場合は、 $$ AABA s_1 \to AAB s_0 \to AA s_0 \to A s_1 \to s_0 $$ となるので、明かりは消えることになる。 そして、いずれかの階のスイッチの状態を $A$から$B$、または $B$から$A$に切り替えると、電灯の状態が反転するのはすぐ確かめられる。 ここで、どの階段のスイッチも同じ振舞いをするので、$A$ と $B$ を並べる順番が結果に影響してはいけないが、上の表式はその性質を満たしている。
以上のように、階段のスイッチの問題は、上記のような2つの状態$\{A,B\}$を持つスイッチの組み合わせとして抽象化することができる。
が、一体、このように考えることで、何か理解の助けになるものなのだろうか?
置換については、参考書のA.2 写像(p. 191)、4.1 カードマジック(p.109)を参照。
ここで、回路の状態 $s_0$ を 0、$s_1$ を 1 とすると、上記の $A$ は置換(互換) $$ A = \begin{pmatrix}0 & 1\\1 & 0\end{pmatrix} $$ に(上段の0は下段の1に、1は0に、それぞれ写像)、$B$は恒等置換(単位置換) $$ B = \begin{pmatrix}0 & 1\\0 & 1\end{pmatrix} $$ に(上段の0は下段の0に、1は1に、それぞれ写像)ちょうど対応することが分かる。
あるいは、状態 $s_0$ を ベクトル $\left( \begin{array}{c} 0 \\ 1 \end{array} \right)$ に、$s_1$をベクトル $\left( \begin{array}{c} 1 \\ 0 \end{array} \right)$ に対応させれば、$A$, $B$を行列 $$ \begin{array}{c} A = \begin{pmatrix}0 & 1\\1 & 0\end{pmatrix}\\ B = \begin{pmatrix}1 & 0\\0 & 1\end{pmatrix} \end{array} $$ と見なし、スイッチの操作を行列の積として表現することも可能である。
いずれの場合でも、$A$と$B$は期待したとおりの状態の変化を生じさせ、$A$と$B$の操作(『掛け算』)の順序が結果に影響しないことも明らかである。 そして、 操作 $A$ を実現するには『逆転』、$B$ は『そのまま』を実現すれば良いのだから、それを回路で表現すると、階段のスイッチは以下の2つの状態(AとB)
この種のスイッチは4路スイッチ(4-way switch)として市販されている。
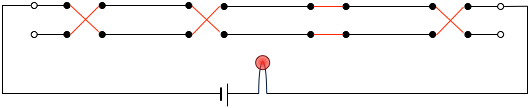
が切り替えられれば良いことになる。このスイッチを使うと、例えば、四階建ての配線の様子(スイッチの状態が A, A, B, A の場合)は以下のようになる:
あみだくじの要領で配線を辿ると、たしかに、図の状態で電気は通じていないが、どこかのスイッチの状態を反転させると通電することがわかる。
以上のように、現実の問題を記号や数値を使いながら抽象化(abstraction)し、計算や記号の操作に翻訳し直して考えるのが、 参考書の主題でもあるコンピュテーショナル・シンキングの第一ステップである。
そして、このように問題をあらかじめ抽象化することで、例えば、五階建てになっても、一般に$N$階のビルの場合でも、同じルールで階段灯の設計をすることが可能となる。
 練習:点灯の状態を増やす
練習:点灯の状態を増やす
階段の各階に3つの状態が可能な(3つのボタンの中からひとつを選択できる)スイッチがあるとしよう。 照明の状態にも3種類あって(消灯、白色、赤色)あって、現在押されていないボタンのひとつを押すと 消灯→白→赤 の順に、 他方のボタンを押すと 消灯→赤→白 の順に、状態が変化するようにしたい。 2状態(消灯と点灯)の場合を参考に、スイッチの構造と配線を設計してみなさい。
 ヒント
ヒント
ボタンの3つの状態を、照明の3つの状態の置換(位数3の巡回群の元)に対応させればよい。
 練習:あみだくじ
練習:あみだくじ
紙にあみだくじを描き、それを置換(互換の組み合わせ)として表現してみなさい。
3. ISBNのチェックディジット
市販されている本の裏面には、ISBN (International Standard Book Number)と呼ばれる数字の並びと、対応するバーコードが印刷されている。 たとえば、この授業の参考書『コンピュテーショナルシンキング』のISBNコードは
9784320123984
である。 最近発売されている書籍にはこのように13桁のISBNコード(ISBN13)が付与されており、世界中の書籍に重複なく付番されている。 書籍の購入サイトの検索画面でISBNを入力すると、(ほとんどの場合)その本がすぐに見つかるはずである。
ISBNのその他の桁にも固有の役割があるので調べてみるとよい。
ISBN13の最後(一番右側)の桁(上記の例では 4 )は、チェックディジットと呼ばれ、そのISBNコードが正しいかどうかの簡単なチェック機能の役割を果たしている。 世の中エラーはつきものであるから、コードを入力した段階でミスを検出できれば、無駄な仕事をせずに済む。 間違ったISBNが入力されたとして、後から「そんな本は販売されていない」ことが判るよりは、 バーコードリーダーやパソコンで入力した時点で「間違いがあります」と教えてもらえるほうが、ずっと効率的であろう。 そんなとき、ISBNのチェックディジットを調べることで、ミスを発見できる。
上の例では、最初の12桁(978432012398)が書籍を表し、その12桁をあるルールに従って計算することでチェックディジット(4)が決まる。 そのルールは以下の通りである。
ISBN13のチェックディジットの計算
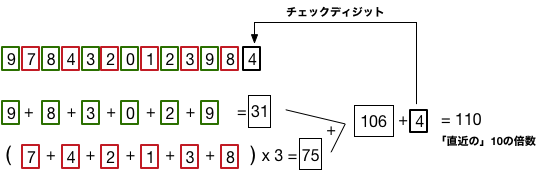
1: 左から数えて奇数番目の桁の総和を求める: $9+8+3+0+2+9=31$
2: チェックディジットを除いて、左から偶数番目の桁の総和を求め、3倍する: $(7+4+2+1+3+8)\times3=25 \times 3=75$
3: 二つの結果を加える: $31 + 75 = 106$
4: 加えた結果にある数 $x$ を加えて10の倍数になるようにする: $106 + x = 110$
5: $x$をチェックディジットとする:$x = 4$
このように、データの一部に、そのデータの「正しさ」をチェックするための情報を含める手法は、データの記憶や通信でよく使われている。 さらに詳しくは、参考書 p.145 「4.3 ディジタルの傷を癒やす」を参照のこと。
 練習:チェックディジットの生成方式
練習:チェックディジットの生成方式
- 偶数番目と奇数番目の桁で計算方法を変えることで、どのようなタイプの入力ミス(エラー)を検知できるようになると期待できるか。
- 偶数番目の総和の「倍率」を3以外にした場合(例えば2や5)、どのような不都合が生じると考えられるか。