Pythonプログラミング（変分法）

このページでは、理工学の様々な場面で登場する変分法について、光の屈折を例として復習する。

１．光の屈折とフェルマーの原理

真空中を光は毎秒約30万キロメートル（地球を７周半）進むことは良く知られている。 一方で、水やガラスなどの物質中を光が通過する際は、物質との相互作用によって、その速度が遅くなる。 水面やレンズなどで光が屈折するのはそのためである。

屈折の度合いには屈折率（refractive index)という指標が用いられる。

屈折率は、真空中での光速に対する物質中の光速の比率として定義され、物質毎に異なる値を持ち、温度などの条件によっても変化する。 物質中の光速を基準（分母）とするので、一般に、１よりも大きな値を取る。 つまり、真空中の光速を $c$ 、屈折率を $n$ とすれば、物質中での光速は $c/n$ ということになる。

位置 $\boldsymbol{r}$ での屈折率を $n(\boldsymbol{r})$ とし、その場所で光が $dr$ だけ進むに要する時間 $dt$ は $$ dt = \frac{n(\boldsymbol{r})}{c} dr $$ となる。 光の経路を、光路長 $s$ を用いて $\boldsymbol{r}(s)$ と表記することにすると、 $\boldsymbol{r}(s_0)$から「発射」された光が $\boldsymbol{r}(s_1)$ まで到達するまでの経路は、それに要した時間、すなわち $$ T = \frac{1}{c} \int_{s_0}^{s_1} n(\boldsymbol{r}(s)) ds $$ が最小となるように「選ばれる」（フェルマーの原理）。 ここで $c$ は定数なので、上記の積分が最小となる経路が問題となる。

光路を（必ずしも光路長には一致しない）媒介変数 $\xi$ を用いて $$ \boldsymbol{r}(s(\xi)) $$ と表記してみる。光路長 $ds$ との間には $$ ds = \left| \boldsymbol{\dot{r}}(\xi) \right| d \xi $$ の関係がある。ここで、$\boldsymbol{\dot{r}}(\xi) = \frac{d \boldsymbol{r}}{d \xi}$。すると、問題の積分は $$ I = \int_{\xi_0}^{\xi_1} n(\boldsymbol{r}(\xi)) \left| \boldsymbol{\dot{r}}(\xi) \right| d \xi $$ である。（$\boldsymbol{r}(s_0) = \boldsymbol{r}(\xi_0), \, \boldsymbol{r}(s_1) = \boldsymbol{r}(\xi_1)$)。

次に、 光路を $r(\xi)$ から少しだけずらして $\boldsymbol{r}(\xi) + \delta \boldsymbol{r}(\xi))$ にしたときの到達時間（あるいは光学的距離）、 すなわち、 $$ \int n( \boldsymbol{r}(\xi) + \delta \boldsymbol{r}(\xi)) \left| \boldsymbol{\dot{r}}(\xi) + \delta \boldsymbol{\dot{r}}(\xi)) \right| d \xi $$ について考える。 ただし、光路の両端は「ずらさない」、すなわち $\delta \boldsymbol{r}(\xi_0) = \delta \boldsymbol{r}(\xi_1) = \boldsymbol{0}$ とする。 ここで、積分の中を $\delta \boldsymbol{r}$ および $\delta \boldsymbol{r}'$ について一次まで展開すると、それぞれのパーツは $$ n( \boldsymbol{r} + \delta \boldsymbol{r} ) \approx n(\boldsymbol{r}) + \nabla n \cdot \delta \boldsymbol{r} + \textrm{h.o.} $$ $$ \begin{eqnarray} \left| \boldsymbol{\dot{r}} + \delta \boldsymbol{\dot{r}} \right| = \sqrt{ \left( \boldsymbol{\dot{r}} + \delta \boldsymbol{\dot{r}} \right) \cdot \left( \boldsymbol{\dot{r}} + \delta \boldsymbol{\dot{r}} \right) } \\ \approx \sqrt{ \boldsymbol{\dot{r}} \cdot \boldsymbol{\dot{r}} } + \frac{\boldsymbol{\dot{r}} \cdot \delta \boldsymbol{\dot{r}}}{\sqrt{ \boldsymbol{\dot{r}} \cdot \boldsymbol{\dot{r}} }} + \textrm{h.o.} \end{eqnarray} $$ となる。 これらを使うと、経路を変更したことに伴う一次の変化量（変分）は $$ \delta I = \int \nabla n(\boldsymbol{r}(\xi)) \cdot \delta \boldsymbol{r}(\xi) \left| \boldsymbol{\dot{r}}(\xi) \right| + n(\boldsymbol{r}(\xi)) \frac{\boldsymbol{\dot{r}}(\xi) \cdot \delta \boldsymbol{\dot{r}}(\xi) }{\left| \boldsymbol{\dot{r}}(\xi) \right|} d \xi $$ となる。 被積分関数の２つ目の項を部分積分（$\delta \boldsymbol{\dot{r}}(\xi)$を積分）し、両端で$\delta \boldsymbol{r}=0$ である条件を課すと、 $$ \begin{eqnarray} \delta I = \int \nabla n(\boldsymbol{r}(\xi)) \cdot \delta \boldsymbol{r}(\xi) \left| \boldsymbol{\dot{r}}(\xi) \right| - \frac{d}{d \xi} \left\{ n(\boldsymbol{r}(\xi)) \frac{\boldsymbol{\dot{r}}(\xi) }{\left| \boldsymbol{\dot{r}}(\xi) \right|} \right\} \cdot \delta \boldsymbol{r}(\xi) \; d \xi \\ = \int \left[ \nabla n(\boldsymbol{r}(\xi)) \left| \boldsymbol{\dot{r}}(\xi) \right| - \frac{d}{d \xi} \left\{ n(\boldsymbol{r}(\xi)) \frac{\boldsymbol{\dot{r}}(\xi) }{\left| \boldsymbol{\dot{r}}(\xi) \right|} \right\}\right] \cdot \delta \boldsymbol{r}(\xi) \; d \xi \end{eqnarray} $$ となる。 $\delta \boldsymbol{r}(\xi)$によらず、これが0となる($I$を停留させる）条件として、最短時間の光路を与える微分方程式（オイラー方程式） $$ \nabla n(\boldsymbol{r}(\xi)) \left| \boldsymbol{\dot{r}}(\xi) \right| - \frac{d}{d \xi} \left\{ n(\boldsymbol{r}(\xi)) \frac{\boldsymbol{\dot{r}}(\xi) }{\left| \boldsymbol{\dot{r}}(\xi) \right|} \right\} = 0 $$ を得る。 ここで、 $$ \frac{d}{ds} = \frac{1}{\left| \boldsymbol{\dot{r}}(\xi) \right|} \frac{d}{d \xi} $$ であったことを思い出して、変数を再び経路長$s$に戻してみると $$ \nabla n(\boldsymbol{r}(s)) - \frac{d}{d s} \left( n(\boldsymbol{r}(s)) \frac{d\boldsymbol{r}(s)}{ds} \right) = 0 $$ が得られる。

屈折のシミュレーション

二次元デカルト座標の場合 $\boldsymbol{r}(s) = (x(s),y(s))$ を考えると、屈折率の分布 $n(x,y)$ に対して、 $$ \begin{eqnarray} \frac{\partial n}{\partial x} - \left( \frac{\partial n}{\partial x} \frac{dx}{ds} + \frac{\partial n}{\partial y} \frac{dy}{ds} \right) \frac{dx}{ds} - n \frac{d^2 x}{ds^2} = 0 \\ \frac{\partial n}{\partial y} - \left( \frac{\partial n}{\partial x} \frac{dx}{ds} + \frac{\partial n}{\partial y} \frac{dy}{ds} \right) \frac{dy}{ds} - n \frac{d^2 y}{ds^2} = 0 \\ \end{eqnarray} $$ が光路を与える微分方程式である。 これを適切な初期条件を与えて解くことによって、光が進む経路を得ることができる。

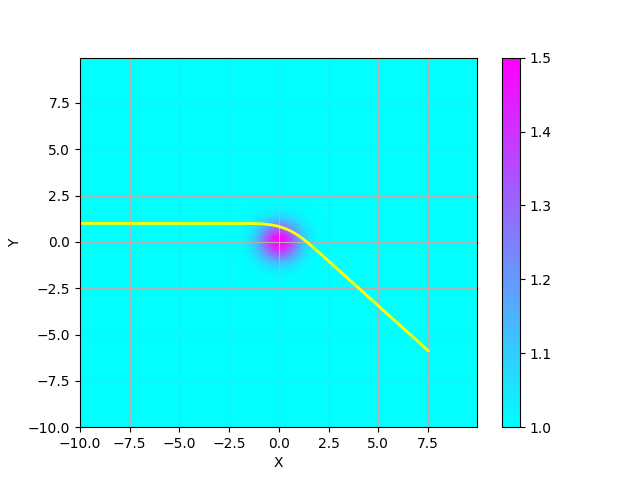
ここでは、原点の周りに屈折率が大きいスポットが $$ n(x,y) = 1 + \frac{\exp(-x^2-y^2)}{2} $$ のように分布していると仮定する。 そこに、$(x,y)= (-10,1.0)$から、x軸に平行な光線が入射する場合の光路を計算し、プロットするコードの例を以下に示す。

オイラー方程式は二階の連立微分方程式であるので、$x, y, \frac{dx}{ds}, \frac{dy}{ds}$ の４つの変数の経路長に沿った変化を計算する必要がある。 その際、ここでは、簡単なオイラー差分を使って、各変数の時間発展を計算している （正確には、同じ計算ステップ内で更新された値を用いているので、一種の リープフロッグ法になっている）。

# coding: utf-8

import math
import numpy as np
import matplotlib.pyplot as plt

def refind(x,y):
    return 1 + 0.5 *  math.exp(- x**2 - y**2)

def gradx(x,y):
    return -x*math.exp(-x**2 - y**2)

def grady(x,y):
    return -y*math.exp(-x**2 - y**2)


xs = []
ys = []

x = -10
y = 1.0

xs.append(x)
ys.append(y)

s = 0
ds = 0.1
dxds = 1
dyds = 0

while s < 20:
    d2xds2 = (1.0/refind(x,y))* (gradx(x,y) - (gradx(x,y)*dxds + grady(x,y)*dyds)*dxds)
    d2yds2 = (1.0/refind(x,y))* (grady(x,y) - (gradx(x,y)*dxds + grady(x,y)*dyds)*dyds)
    dxds += d2xds2 * ds
    dyds += d2yds2 * ds
    x += dxds * ds
    y += dyds * ds
    xs.append(x)
    ys.append(y)
    s += ds

X,Y = np.meshgrid(np.arange(-10, 10, 0.05),np.arange(-10, 10, 0.05))
Z = 1 + 0.5 * np.exp(-np.square(X)-np.square(Y))
plt.pcolormesh(X, Y, Z, cmap='cool')
plt.colorbar(orientation="vertical")
plt.plot(xs,ys, color=(1.0,1.0,0.0), linewidth=2.0)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()

　練習： 直線的な界面

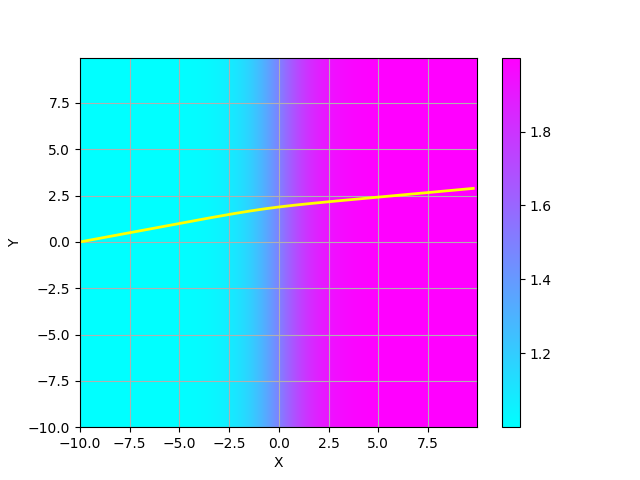
y軸に平行な直線的な境界（界面）を想定し、屈折率の分布が $$ n(x,y) = 1 + \frac{\Delta n}{1 + \exp(-x)} $$ のような場合に、界面に斜めに入射する光線の経路をシミュレーションしてみなさい。

さらに、光の入射角と屈折角と、$\Delta n$との関係についても調べてみなさい。 以下に実行例を示した。

　解説: スネルの法則

屈折率がxのみに依存する場合に、光路を与える微分方程式は $$ \frac{\partial n(x)}{\partial x} \frac{dx}{ds} \frac{dy}{ds} - n(x) \frac{d^2 y}{ds^2} = 0 $$ となるが、この式は $$ \frac{d}{ds} \left[ n(x) \frac{dy}{ds} \right] = 0 $$ に他ならない。 すなわち、光路を通じて、ある一定となる量（保存量）$C$が存在して $$ n(x(s)) \frac{dy(s)}{ds} = C $$ となる。

ここで、$\theta$をx軸からの角度（ラジアン）とすれば、定義より $\frac{dy}{ds} = \sin \theta$ であるから $$ n(s) \sin \theta(s) = C $$ これはスネルの法則（を連続な界面に拡張したもの）に他ならない。

上記の光の屈折の問題は、ラグランジアン $L$ を $$ L(x,y,\dot{x},\dot{y}) = n(x,y) \sqrt{ \dot{x}^2 + \dot{y}^2} $$ とおいたときの変分問題であって、そのオイラー・ラグランジュ方程式 $$ \begin{eqnarray} \frac{\partial L}{\partial x} - \frac{d}{d\xi} \frac{\partial L}{\partial \dot{x}} = 0 \\ \frac{\partial L}{\partial y} - \frac{d}{d\xi} \frac{\partial L}{\partial \dot{y}} = 0 \\ \end{eqnarray} $$ が光路の「運動方程式」を与えている。

y軸に平行な界面が存在するような場合、座標を$y+\delta y$だけずらしても、ラグランジアンは不変であるから $$ \delta L = L(x,y+\delta y,\dot{x},\dot{y} + \delta \dot{y} )- L(x,y,\dot{x},\dot{y}) =0 $$ である。ここで、オイラー・ラグランジュ方程式を使いながら、$\delta L$を具体的に書き下すと $$ \begin{eqnarray} \delta L &=& \frac{\partial L}{\partial y} \delta y + \frac{\partial L}{\partial \dot{y}} \delta \dot{y}\\ &=& \left\{ \frac{d}{d \xi} \frac{\partial L}{\partial \dot{y}} \right\} \delta y + \frac{\partial L}{\partial \dot{y}} \delta \dot{y} \\ &=& \frac{d}{d \xi} \left\{ \frac{\partial L}{\partial \dot{y}} \delta y \right\} \\ &=& \frac{d}{d \xi} \left\{ n(x,y) \frac{ \dot{y}}{\sqrt{ \dot{x}^2 + \dot{y}^2}} \delta y \right\} = 0 \end{eqnarray} $$ ここで、$\delta y$は定数であることと（そもそも$\delta \dot{y}=0$）、定義から $$ \frac{ \dot{y}}{\sqrt{ \dot{x}^2 + \dot{y}^2}} = \frac{dy}{ds} $$ であったから、 $$ n \frac{dy}{ds} = C $$ が再び得られた。

以上を言い換えると、スネルの法則は、界面の並進対称性に伴ってネーターの定理から帰結される保存則*である。

重力による光の曲がり

弱い球対称な重力場を考える。 質量中心から距離$r$の点での計量は近似的に $$ ds^2 = \left(1 - \frac{r_g}{r} \right) c^2 dt^2 - \left(1 + \frac{r_g}{r} \right)(dx^2 + dy^2 + dz^2) $$ のように表されることが分かっている。 ここで$r_g$は重力半径あるいはSchwarzchild半径と呼ばれ、重力定数を$G$、質量を$m$とすると $r_g = 2 G m/c^2$で与えられる。

光は$ds=0$であるような測地線（ヌル測地線）に沿って伝搬するため $$ 0 = \left(1 - \frac{r_g}{r} \right) c^2 dt^2 - \left(1 + \frac{r_g}{r} \right)(dx^2 + dy^2 + dz^2) $$ 光の見かけ上の速度を$u$おくと、 $r_g/r \ll 1$ では、 $$ u^2 = \frac{dx^2 + dy^2 + dz^2}{dt^2} = c^2 \frac{1 - \frac{r_g}{r}}{1 + \frac{r_g}{r}} \approx c^2 \left( 1 - 2 \frac{r_g}{r} \right) $$ のように振る舞うことが分かる。 すなわち、球対称な弱い重力場は $r$ の位置での屈折率が $$ n(r) = \frac{1}{ \left(1 - \frac{2 r_g}{r} \right)^{1/2}} \approx 1 + \frac{r_g}{r} $$ の媒質のように振る舞う。

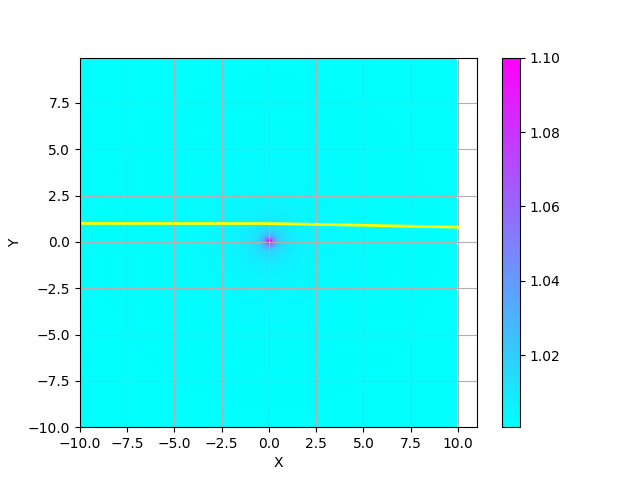
そこで、前節と同じコードで、ただし、屈折率の分布のみを変えてみた例を以下に示す：

import math
import numpy as np
import matplotlib.pyplot as plt

rg=0.01

def refind(x,y):
    return 1 + rg/math.sqrt(x**2+y**2)

def gradx(x,y):
    d = math.sqrt(x**2+y**2)**3
    return -rg*x/d

def grady(x,y):
    d = math.sqrt(x**2+y**2)**3    
    return -rg*y/d

xs = []
ys = []

x = -10
y = 1.0

xs.append(x)
ys.append(y)

s = 0
ds = 0.01
dxds = 1
dyds = 0

while s < 20:
    d2xds2 = (1.0/refind(x,y))* (gradx(x,y) - (gradx(x,y)*dxds + grady(x,y)*dyds)*dxds)
    d2yds2 = (1.0/refind(x,y))* (grady(x,y) - (gradx(x,y)*dxds + grady(x,y)*dyds)*dyds)
    dxds += d2xds2 * ds
    dyds += d2yds2 * ds
    x += dxds * ds
    y += dyds * ds
    xs.append(x)
    ys.append(y)
    s += ds

X,Y = np.meshgrid(np.arange(-10, 10, 0.05),np.arange(-10, 10, 0.05))
Z = np.clip( 1 + rg/np.sqrt(np.square(X)+np.square(Y)), 1.0, 1.1)
plt.pcolormesh(X, Y, Z, cmap='cool')
plt.colorbar(orientation="vertical")
plt.plot(xs,ys, color=(1.0,1.0,0.0), linewidth=2.0)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()