「Pythonプログラミング」（その他のトピック・三体問題）

Pythonプログラミング（三体問題）

このページでは、惑星運動のシミュレーションを試みる（ここはこれから）。

１．惑星の運動

質量 $m_1$ の物体1の位置ベクトルを $\boldsymbol{r}_1$ , 質量 $m_2$ の物体2の位置ベクトルを $\boldsymbol{r}_2$ とすると、物体1に働く重力は、万有引力定数を$G$とすると $$ \boldsymbol{F}_{21} = G m_1 m_2 \frac{\boldsymbol{r}_2 - \boldsymbol{r}_1}{\left| \boldsymbol{r}_2 - \boldsymbol{r}_1 \right|^3} $$ であり、物体1に働く力がこれ以外に無いとすると、物体1の運動方程式は $$ m_1 \frac{d^2 \boldsymbol{r}_1}{dt^2} = \boldsymbol{F}_{21} $$ であり、物体2については、作用反作用の法則から反対向きの力が作用することから、運動方程式は $$ m_2 \frac{d^2 \boldsymbol{r}_2}{dt^2} = \boldsymbol{F}_{12} = - \boldsymbol{F}_{21} $$ となる。

物体が複数あるときも同様で、$j$番目の物体から$i$番目の物体に作用する重力は $$ \boldsymbol{F}_{ji} = G m_i m_j \frac{\boldsymbol{r}_j - \boldsymbol{r}_i}{\left| \boldsymbol{r}_j - \boldsymbol{r}_i \right|^3} $$ であり、$i$番目の物体の運動方程式は $$ m_i \frac{d^2 \boldsymbol{r}_i}{dt^2} = \sum_{j \ne i} \boldsymbol{F}_{ji} $$ と書ける。 $m_i$は左右両辺に共通に現れるため相殺し、結果、重力場中の運動は物体$i$自身の質量には依らないことがわかる。

方程式の無次元化

これらを踏まえて、太陽と地球と月の運動のシミュレーションを行ってみよう。簡単のため、他の惑星の効果は無視できるとする。その際に、地球の公転を基準にものごとを考えることにする。

まず、地球と太陽の平均的な距離 $R$ (14959万km)を長さの単位とする（これを天文単位 auと呼ぶ）。太陽の質量を$M$とし、地球の軌道を半径$R$の円とすれば、ケプラーの第三法則から、地球の公転周期$T$は $$ \frac{R^3}{T^2} = \frac{G M}{4 \pi^2} $$ となるので、時間については $$ T = \frac{2 \pi R^{3/2}}{(G M)^{1/2}} $$ を単位とする。具体的には $$ \begin{eqnarray} \boldsymbol{r} = R \boldsymbol{\xi} \\ \boldsymbol{t} = T \tau \end{eqnarray} $$ とおいて、無次元量 $\boldsymbol{\xi}$ と $\tau$ を変数とする運動方程式を考えればよい。

具体的に式を整理すると $$ \frac{ d^2 \boldsymbol{\xi}_i }{d \tau^2} = \sum_{j \ne i} 4 \pi^2 \left( \frac{m_j}{M} \right) \frac{\boldsymbol{\xi}_j - \boldsymbol{\xi}_i}{\left| \boldsymbol{\xi}_j - \boldsymbol{\xi}_i \right|^3} $$ となる。すると、初期条件以外に必要なパラメータは、地球と月の太陽との質量比ということになって、 $$ \begin{eqnarray} \frac{m_e}{M} \approx 3.00 \times 10^{-6} \\ \frac{m_m}{M} \approx 0.037 \times 10^{-6} \end{eqnarray} $$ であることが知られている($m_e$は地球、$m_m$は月の質量）。

２．太陽と地球と月のシミュレーション

月の影響が無視できる場合、前節の単位での地球の軌道速度は $2 \pi$ になる（半径1の円軌道を1単位時間かけて運動しているため）。一方、月の地球の距離は約38.5万kmであるから、前節で導入した単位では $38.5/14959 \approx 0.00257$ となる。また、地球を中心にした座標でみると、月は約27.29日で地球の周りを公転している。

これらを考慮しながら、太陽を原点に、$z=0$の平面上での３天体の運動を１年分シミュレーションするコードの例を以下に示した。

# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

FPSQ = 4*math.pi**2
Ke = 3.00e-6
Km = 0.037e-6

def eq_motion(t, x):
    xs = x[0] ; ys = x[1] ; vxs = x[2] ; vys = x[3]
    xe = x[4] ; ye = x[5] ; vxe = x[6] ; vye = x[7]
    xm = x[8] ; ym = x[9] ; vxm = x[10] ; vym = x[11]
    Rse = math.sqrt((xs-xe)**2 + (ys-ye)**2)
    Rem = math.sqrt((xe-xm)**2 + (ye-ym)**2)
    Rsm = math.sqrt((xs-xm)**2 + (ys-ym)**2)    
    dxsdt = vxs
    dysdt = vys
    dvxsdt = FPSQ*Ke*(xe-xs)/Rse**3 + FPSQ*Km*(xm-xs)/Rsm**3
    dvysdt = FPSQ*Ke*(ye-ys)/Rse**3 + FPSQ*Km*(ym-ys)/Rsm**3
    dxedt = vxe
    dyedt = vye
    dvxedt = FPSQ*(xs-xe)/Rse**3 + FPSQ*Km*(xm-xe)/Rem**3 
    dvyedt = FPSQ*(ys-ye)/Rse**3 + FPSQ*Km*(ym-ye)/Rem**3 
    dxmdt = vxm
    dymdt = vym
    dvxmdt = FPSQ*(xs-xm)/Rsm**3 + FPSQ*Ke*(xe-xm)/Rem**3 
    dvymdt = FPSQ*(ys-ym)/Rsm**3 + FPSQ*Ke*(ye-ym)/Rem**3     
    return [dxsdt, dysdt, dvxsdt, dvysdt,
            dxedt, dyedt, dvxedt, dvyedt,
            dxmdt, dymdt, dvxmdt, dvymdt]

dt = 0.0001

ve = 2*math.pi
dem = 38.5/14959
vm = 2*math.pi*dem/(27.29/365.0)

init_vals=[0, 0, 0, 0,
           1, 0, 0, ve,
           1-dem, 0, 0, ve+vm]
span = (0.0,1.0)
steps = np.arange(0.0, 1, dt)
args=()
res = solve_ivp(eq_motion, t_span=span, y0=init_vals, t_eval=steps,
                method='LSODA', rtol=1.0e-6, atol=1.0e-15, args=args)
xs = res.y[0,:]
ys = res.y[1,:]
xe = res.y[4,:]
ye = res.y[5,:]
xm = res.y[8,:]
ym = res.y[9,:]

plt.plot(xs,ys, color=(1.0,0.5,0.0), linewidth=1.0)
plt.plot(xe,ye, color=(0.0,0.5,1.0), linewidth=0.5)
plt.plot(xm,ym, color=(0.5,0.5,0.5), linewidth=0.5)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()

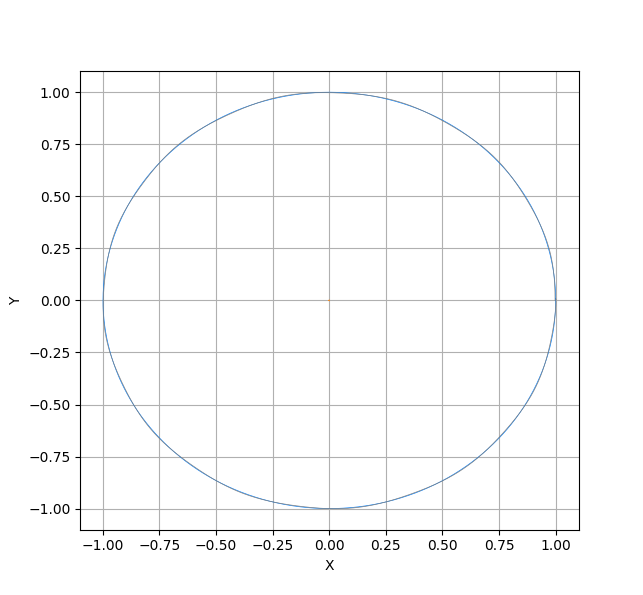
このコードを実行すると、太陽（赤色）は原点でほぼ動かず、また、地球と月の軌道はほとんど重なり合って表示される。

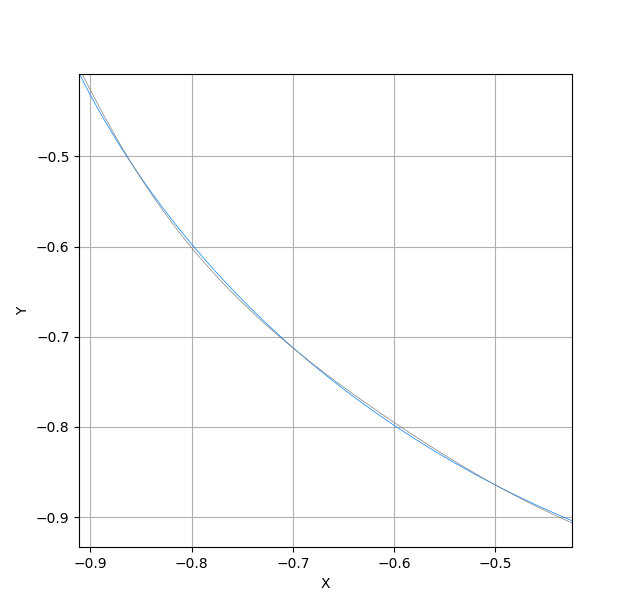
地球と月の軌道を部分的に拡大すると、以下のように、太陽との距離関係が入れ違いながら運動していることが確認できる。月が地球の周りを「周回」しているというよりは、双子（親子？）の惑星が太陽の周りを回っている、と表現したほうが適切にも感じられる。その一方で、地球と月は同様に太陽の重量の影響を受けているという点では、ちょうど宇宙ステーションの内部が無重力であるのと同様、無重力中で地球の周りを月が回っている、という捉え方が間違っているわけではない。

　練習：シミュレーション

上記のコードを修正し、地球を中心とした座標で、月がどのように運動しているかを表示してみなさい。

SciPyのsolve_ivpのマニュアルを参考に、method, rtol, atolなどの指定を変えて、結果にどの程度の違いが生じるか実験してみなさい。

　練習：James Webb 宇宙望遠鏡の軌道

James Webb宇宙望遠鏡(質量約6500kg）は、太陽と地球を結ぶ直線上のラグランジュ点（地球の外側を周回する軌道上）で運用される。

NASAの解説なども手がかりに、太陽、地球、宇宙望遠鏡の運動をシミュレーションしてみなさい。