ローレンツモデルとカオス

このページでは、決定論的カオスの初期の例と知られるローレンツモデルをシミュレーションしてみる。

１．対流現象のモデル化

箱の中に水などの流体を入れて、下を温めて、上を冷やすと、対流が起こる。 具だくさんではない味噌汁を、熱いうちに上から眺めると、味噌の濃淡が生じているのが確認できるが、それも対流の仕業である。

こうした対流現象は、ナビエ・ストークス方程式と熱拡散方程式と呼ばれる偏微分方程式、そして、流体の状態方程式を連立させて解くことで、説明することができる。 近年の天気予報は大気の流れやそこで生じる状態変化を計算モデルによって数値シミュレーションすることによって行われているが、 基本的には同様の計算を大規模かつ複雑化したものと言える。

平行平板の中に流体を閉じ込めて、上下に温度差をつけると、温度差が小さいうちは、熱は熱伝導（拡散）によって運ばれ、流れ（対流）は生じない。 というのは、流体の粘性（壁や流体同士に働く摩擦）の効果が支配的となるからである。 温度差がある値を超えると、温められた下方の流体は浮力によって上昇し、相対的に冷めた上方の流体は下降を始める。 すなわち、粘性力よりも浮力が支配的になって対流が生じる。

大気変動を単純化したモデルとして、気象学者のE. N. Lorenz は対流運動を単純化した微分方程式を考案し調べた。 モデルの導出には専門的な知識と少々面倒な計算が必要なのでここでは割愛し、その結果のみを示すことにする。

Lorentzは、流体の状態を時間に依存する３つの変数（$X(t), Y(t), Z(t)$）で表現した。 $X$は対流が回転する速度、 $Y$は温度場の上下方向の定常分布からのずれ、 $Z$は温度場の水平方向の定常分布からのずれ、 にそれぞれ対応する。

まず、対流の回転($X$)は上下方向の温度差($Y$) に比例した浮力で駆動されるが、粘性で緩和される効果を、微分方程式 $$ \frac{dX}{dt} = p (Y-X) $$ で表現する。 ここで、$p$はプラントル数（動粘性係数/熱拡散係数）に対応した正値のパラメータである。

上下方向の温度差の定常分布からのずれ$Y$は、浮力による流体の運動で増強されるが、水平方向の温度差の不均一が対流（回転）することで緩和される。 また、熱拡散によっても緩和される。その様子を $$ \frac{dY}{dt} = r X - X Z - Y $$ で表現する。 ここで、$r$はレイリー数（浮力/熱拡散係数）に比例する正値のパラメータである。 レイリー数は流体の密度、粘性、熱拡散係数に依存し、また、上下の温度差に比例し、平板の間隔の３乗に比例するような無次元量である。

水平方向の温度差の定常分布からのずれ$Z$は、上下方向の分布のずれが対流（回転）することで増強され、熱伝導で緩和される。 その様子を $$ \frac{dZ}{dt} = X Y - b Z $$ で表現する。 ここで$b$は対流セルの幅に関係して正値を取るパラメータである。

以上をまとめた３変数の微分方程式はローレンツ方程式と呼ばれている： $$ \begin{eqnarray} \frac{dX}{dt} & = & p (Y-X) \\ \frac{dY}{dt} & = & r X - X Z - Y \\ \frac{dZ}{dt} & = & X Y - b Z \end{eqnarray} $$

２．ローレンツ方程式のシミュレーション

ローレンツ方程式は一見単純そうに見えるが、その挙動はかなり複雑である。

定常解（固定点）を求めるために $$ \frac{dX}{dt} = \frac{dY}{dt} = \frac{dZ}{dt} = 0 $$ と置いて、$X,Y,Z$についての連立方程式を解いた解を$(X^*,Y^*,Z^*) $とする。 そして、固定点の周りでの解を $X(t) = X^* + x(t), \, Y(t) = Y^* + y(t), \, Z(t) = Z^* + z(t)$と置いて、微分方程式を線形化すると $$ \begin{pmatrix} \dot{x}\\ \dot{y}\\ \dot{z} \end{pmatrix} = \begin{pmatrix} -p & p & 0 \\ r - Z^* & -1 & -X^* \\ Y^* & 0 & -b \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix} $$ となる。

$r \lt 1$の場合は $$ (X^*,Y^*,Z^*) = (0, 0, 0) $$ が唯一の実数解であり、 そこでの行列の固有値を調べると、全て負であることが確認できる。 すなわち、$(0, 0, 0)$は安定な唯一の固定点で、どのような初期値から出発した解軌道も最終的には原点に収束することがわかる。

$r$が1を超えると、 $(0, 0, 0)$は不安定化し、 新たに対の固定点 $\left(\sqrt{b (r-1)}, \sqrt{b (r-1)}, r-1 \right)$, $\left(-\sqrt{b (r-1)}, -\sqrt{b (r-1)}, r-1 \right)$ が生じる。 $r$が小さいうちはこれらふたつの固定点は安定であるが、ある臨界値を超えると不安定化して、その周囲で振動的に振る舞う（リミットサイクルが生じる）ことが知られている。 そして、さらに$r$が大きくなると、カオス(chaos)と呼ばれる、複雑な挙動を呈するようになる。

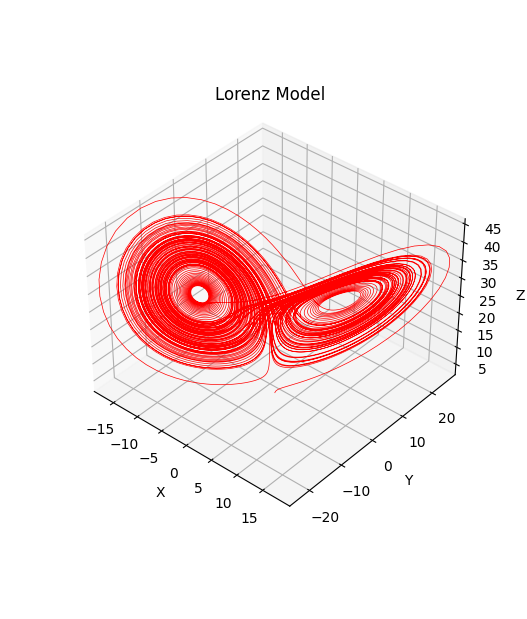
以下に、Lorenzがカオス状態を発見したパラメータの組($p=10, \, r=28, \, b=8/3$)でローレンツ方程式を解き、 解軌道の様子を表示するコードの例を示す。 初期値は$(1,0,0)$に設定した。

# coding: utf-8
import math
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
from scipy.integrate import solve_ivp

p = 10
r = 28
b = 8/3

def lorenz_eq(t, y):
    X = y[0]
    Y = y[1]
    Z = y[2]
    dXdt = p * (Y - X)
    dYdt = r*X - X*Z - Y
    dZdt = X*Y - b*Z
    return [dXdt, dYdt, dZdt]

dt = 0.01
init_vals=[1, 0, 0]
span = (0.0,100.0)
steps = np.arange(0.0, 100, dt)
args=()
res = solve_ivp(lorenz_eq, t_span=span, y0=init_vals, t_eval=steps,
                method='RK45', rtol=1.0e-6, atol=1.0e-12, args=args)
X = res.y[0,:]
Y = res.y[1,:]
Z = res.y[2,:]

ax = plt.axes(projection='3d')
ax.view_init(elev=30, azim=-60) 
ax.plot3D(X, Y, Z, 'red', linewidth=0.5)
ax.set_title('Lorenz Model')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.grid(True)
plt.show()

このコードをPCで実行すると、マウスで視点を変更できる。ノートブック上で実行する場合は ax.view_init(elev=30, azim=-60)の箇所で視点の角度を変更することができる。

軌道の様子を観察すると、蝶の二枚の羽のような狭い領域（アトラクター）の中で、不規則に動いているのが判る。 二枚の羽の中心が、上で述べた対の（不安定化した）固定点になっており、軌道は、一方の固定点の周り（羽の中）で何回か周回したあと、 他方の固定点の周り（羽の中）でまた何回か周回して・・・、を繰り返している。 すなわち、「あちら側」と「こちら側」をランダムにスイッチしているようにも見える。

　解説: カオスの初期値敏感性

ローレンツ方程式は常微分方程式なので、初期値を与えると、その先の未来（解）は一意に決定される。 その一方で、シミュレーション結果をみると、挙動はえらく複雑で、とても予測可能には思えない。 このことはどのように理解したら良いのだろうか。

それを考える際の重要なポイントのひとつがシステムの初期値敏感性である。

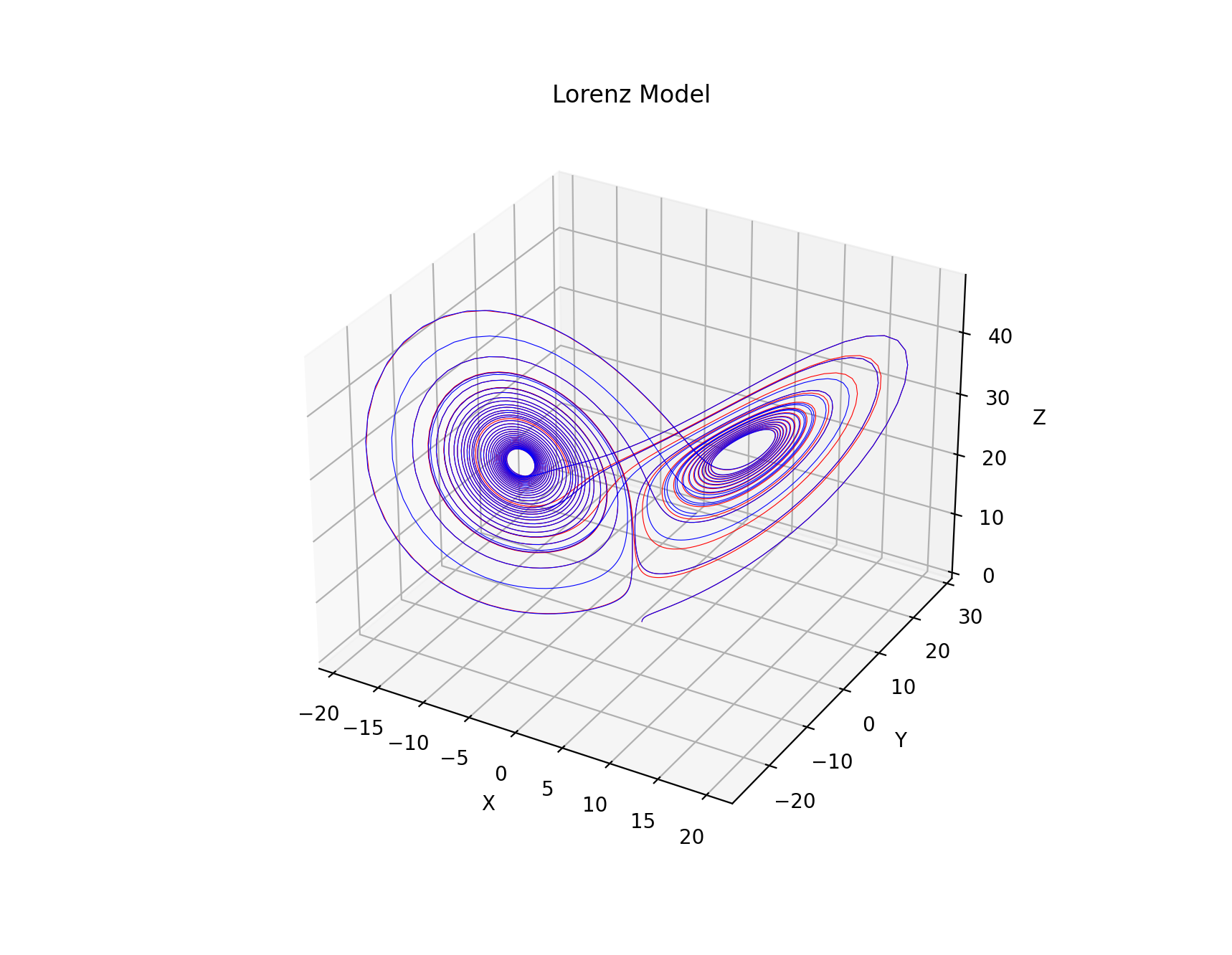
以下のコードは、上記のコードを少しだけ修正して、eps=0.0001しか違わない二種類の初期値から出発して、tmax=35.0までローレンツ方程式を解き、 ふたつの軌道をそれぞれ赤と青でプロットするようにした例である：

import math
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
from scipy.integrate import solve_ivp

p = 10
r = 28
b = 8/3

def lorenz_eq(t, y):
    X = y[0]
    Y = y[1]
    Z = y[2]
    dXdt = p * (Y - X)
    dYdt = r*X - X*Z - Y
    dZdt = X*Y - b*Z
    return [dXdt, dYdt, dZdt]

tmax=35.0
eps=0.0001
dt = 0.01
init_vals1=[1, 0, 0]
init_vals2=[1+eps, 0, 0]
span = (0.0,tmax)
steps = np.arange(0.0, tmax, dt)
args=()
res1 = solve_ivp(lorenz_eq, t_span=span, y0=init_vals1, t_eval=steps,
                method='RK45', rtol=1.0e-6, atol=1.0e-12, args=args)
X1 = res1.y[0,:]
Y1 = res1.y[1,:]
Z1 = res1.y[2,:]

res2 = solve_ivp(lorenz_eq, t_span=span, y0=init_vals2, t_eval=steps,
                method='RK45', rtol=1.0e-6, atol=1.0e-12, args=args)
X2 = res2.y[0,:]
Y2 = res2.y[1,:]
Z2 = res2.y[2,:]

ax = plt.axes(projection='3d')
ax.view_init(elev=30, azim=-60) 
ax.plot3D(X1, Y1, Z1, 'red', linewidth=0.4)
ax.plot3D(X2, Y2, Z2, 'blue', linewidth=0.4)
ax.set_title('Lorenz Model')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.grid(True)
plt.show()

軌道の様子をよく観察すると、いずれも$(1,0,0)$付近から出発したふたつの軌道ははじめは重なり合っているが、 やがて離れはじめている様子が確認できる。 tmaxの値をさらに大きくして、先の時間までシミュレーションすると、赤と青のふたつの軌道は互いに全く関係なかったかのように振る舞うようになる。 すなわち、「ほとんど同じ初期値から出発した」という記憶は比較的短時間のうちに失われてしまうわけである。

　練習: バタフライ効果

上記のコードのepsとtmaxを変えて、ローレンツ方程式の初期値敏感性（バタフライ効果）の様子を観察してみなさい。

solve_ivp()関数に与えるパラメータを変えて、軌道の様子がどのように変わるか（変わらないか）、実験してみなさい。

　練習：ローレンツプロット

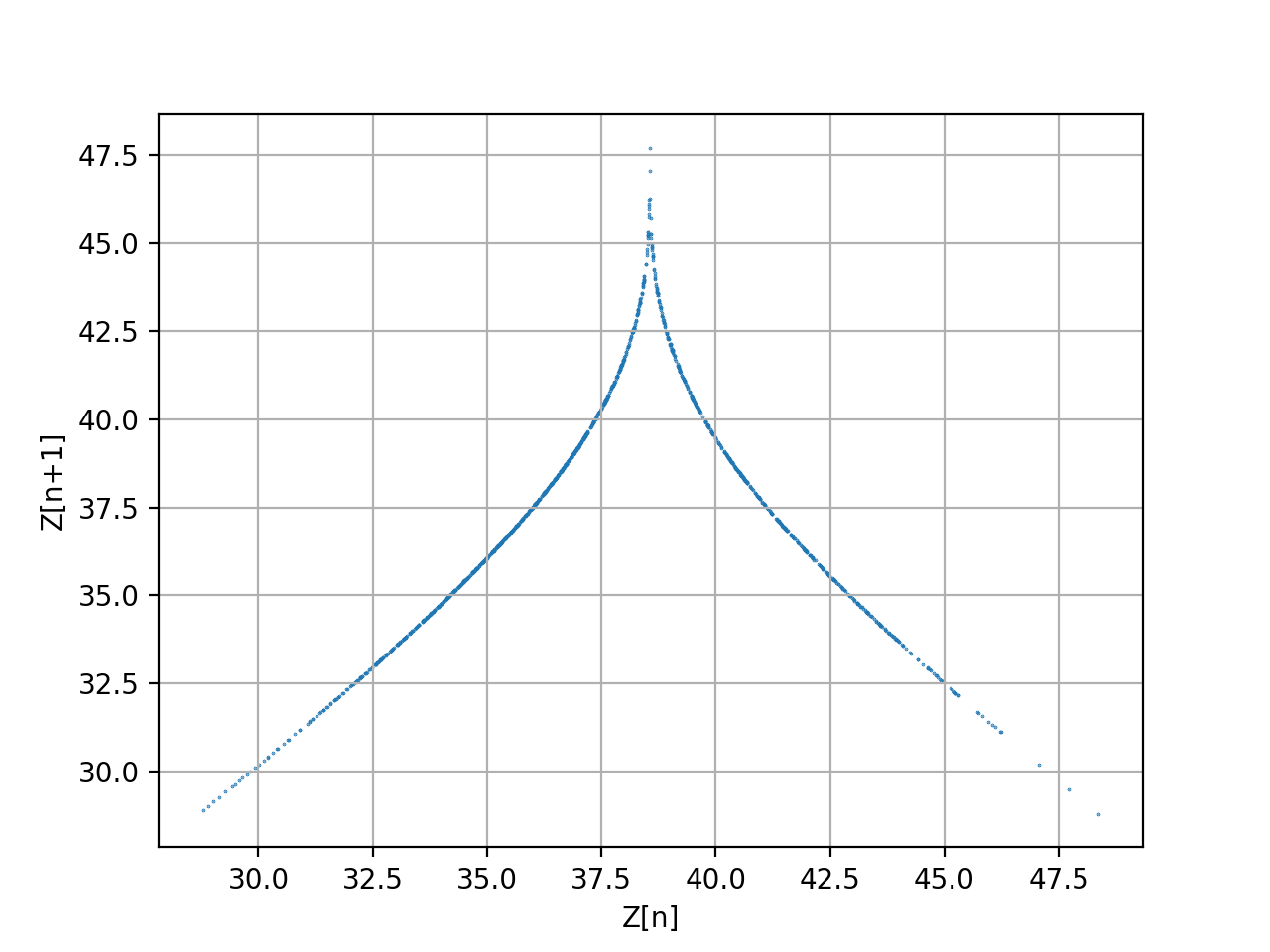
不規則に変動している$Z(t)$が、ある時点$t_n$で最大値をとり、その後減少した後、再び$t_{n+1}$で最大になったとする。 そのとき、横軸に$Z(t_n)$、縦軸に$Z(t_{n+1})$をプロットすると、以下のように「テント」のようなグラフが得られる。 これは、$n$番目の最大値と$n+1$番目の最大値の写像関係を与えるもので、ローレンツプロットと呼ばれている。

上図のようなローレンツプロットを得るコードを作成してみなさい。

　練習：レスラー方程式

ローレンツ方程式と同様に３変数の微分方程式で、カオスアトラクターが出現することで知られるレスラー方程式 $$ \begin{eqnarray} \frac{dX}{dt} & = & -Y - Z\\ \frac{dY}{dt} & = & X + a Y\\ \frac{dZ}{dt} & = & b + Z \, (X-c)\\ \end{eqnarray} $$ を数値シミュレーションして、アトラクターを描画してみなさい。