Pythonプログラミング（テキスト情報のベクトル表現）

(このページは作成中)

非数値的な情報を「ベクトル」として表現する

コンピュータが文字情報を扱う場合は、文字毎にユニークな番号（文字コード）を割り当てて、数値として扱う方法が一般的である。 例えば、ASCIIコードという流儀では、大文字のAは65、Bは66、Zは90、といった具合である。

ここでは簡単のために、アルファベットの大文字に制限して考えることにすると、 AからZまでの26通りが何らかの方法で区別できれば良いのであるから、かなり冗長ではあるけれども、26次元の「ベクトル」を考えて $$ \begin{eqnarray} A = (1,0,0,0,\cdots,0) \\ B = (0,1,0,0,\cdots,0) \\ C = (0,0,1,0,\cdots,0) \\ \end{eqnarray} \vdots $$ のように表現することもできる（一箇所だけ1であることから、この方式は「one-hotベクトル」と呼ばれる）。

文字コードでは数値の違い（大きさ）で区別していた内容を、ベクトル表現では、その方向で区別する点が大きな違いとなる。 そして、こうやって方向で区別することによって、情報の類似の度合いを、ベクトル間の角度（コサイン距離）によって計量することが可能となる。

情報の関係性の抽出

英語の単語を考えてみよう。辞書には沢山の単語が並んでいるが、デタラメにアルファベットを並べてみても、「正しい」 単語になる確率は非常に小さいことはすぐに想像できる。 言い換えれば、アルファベットの並び方にはある種の強い制限、ないしは、規則があるはずだ。

例えば、VIOLINという語を考えてみると、IはVとOに挟まれており、OはIとLに挟まれている。 そこで、（最初と最後の文字を除いて）両隣の文字に着目し、どの文字に挟まれている場合にどの文字が出現しやすいかを調べて、 統計的な規則が無いかを探ってみよう。

このことは、次のように表現することができる： $x,y,z$をアルファベットの文字を表す変数とする。 そして、これらは変数は前節のやり方で（26次元の）ベクトルで表現されているとしよう。 単語中の文字の並び$xzy$に対して、 文字$x,y$が与えられた条件下で文字$z$が出現する確率を $$ P(z|x,y) $$ で表すことし、 さらに、$x,y$ の組から、$n$次元のベクトル $\boldsymbol{w}$ への変換 $\boldsymbol{w} = w(x,y)$ を使って、近似的に $$ P(z|x,y) \approx P(z|\boldsymbol{w}) $$ と書けるような場合を考えてみる。 そんなにうまい変換をどのように見つけるかは別とすれば、 上記は、$n$次元のベクトルと26のべクトルとの（確率的な）対応関係を与える形になっている。

もし、ある$w$に対して、選択的に$z$の出現確率が高ければ、 単語中に登場する文字情報を $n$ 次元のベクトル $\boldsymbol{w}$ で表現し直したことになる。

ニューラルネットによる実装と実験

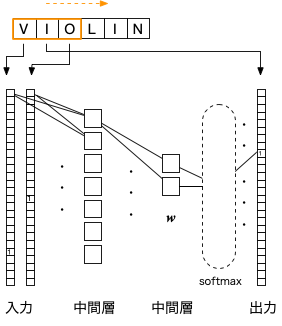
ここで、J. Joyceの小説 Ulysses から抽出した単語のリストwords-ulysses.txtを用意した。 このファイルの各行から単語を読み込んで、単語中の文字の両隣の文字を入力に、中央の文字を出力に対応させ、層状のニューラルネットワークを使って確率分布を学習させてみよう。

図のように、単語ベクトルの次元（26）の倍の入力、１層目の中間層を経て、上記の$w$に対応する中間層、そして、単語ベクトルの次元数の出力を層状に結合する。 文字の出現確率の近似値を表現するため、活性化関数は softmax とする。 そして、単語の中の連続する３文字を取り出し、両端の文字ベクトルを入力に、中央の文字ベクトルを出力の学習データとする。

少し冗長ではあるが、上記をPythonでコーディングした例を示す。この場合、中間層$w$の次元は2としている。

# coding:utf-8
from keras import layers,models
import numpy as np
import matplotlib.pyplot as plt


path='words-ulysses.txt'

with open(path,mode='r',encoding='utf-8') as f:
    lines = f.readlines()

window=1
ndim=2

ndata=0
for words in lines:
    ell = len(words)-window*2
    if ell>0:
        ndata = ndata + ell
    
x_train = np.zeros((ndata,window*2,26),dtype=np.float32)
y_train = np.zeros((ndata,26),dtype=np.float32)

cnt=0
for words in lines:
    w = list(words.strip())
    ch=np.zeros((len(w),),dtype=np.int32)
    for i in range(len(w)):
        ch[i]=ord(w[i])-65
    for i in range(len(w)):
        if i>=window and i<=len(w)-window-1:
            j=0
            for k in range(i-window,i+window+1):
                if k != i:
                    x_train[cnt,j,ch[k]]=1.0
                    j=j+1
            y_train[cnt,ch[i]]=1.0
            cnt=cnt+1
            
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(window*2,26)))
model.add(layers.Flatten())
model.add(layers.Dense(ndim,activation='relu'))
model.add(layers.Dense(26,activation='softmax'))
model.summary()

model.compile(loss='kullback_leibler_divergence',optimizer='rmsprop',metrics=['acc'])

model.fit(x_train,y_train,epochs=5,batch_size=100)

output_layer = model.layers[3] 
wt = output_layer.get_weights()[0]

xdata=[]
ydata=[]
for i in range(26):
    xdata.append(wt[0,i])
    ydata.append(wt[1,i])
    
plt.plot(xdata,ydata,'.', color=(1.0,0,0.0))
for i in range(26):
    txt = chr(i+65)
    plt.annotate(txt,(xdata[i],ydata[i]))
plt.grid(True)
plt.show()

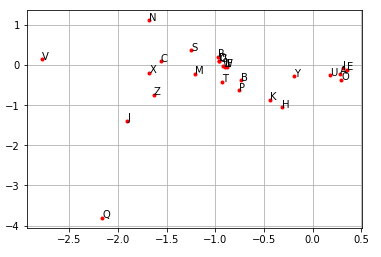
$w$から$i$番目の出力セルへの結合は、$w$の次元（この場合は２本）だけあり、その荷重が$i$番目の文字の出現確率を決めている。 $$ p_i = \frac{\exp\left( \sum_k V_{k,i} w_k\right) }{\sum_k \exp\left( \sum_{k} V_{k,i} w_k) \right) } $$ そこで、このコードを実行すると、中間層$w$から出力層への荷重（上式の$V_{k,i}$）が文字毎にプロットされるようになっている。

以下はその例であるが、母音(A,E,I,O,U)が明らかにクラスターを形成しており、その意味で「同類」であることが表現されている。 つまり、特に先験的な情報無しに、これら５つの文字が母音というベクトルの周りに集約されたことになる。 その他の文字についても、特徴的な「場所」を占めているものがあることがわかる。

単語のベクトル化：word2vec

上記のアイデアは自然に「文」に拡張することができる。 つまり、文字を文を構成する単語に、単語を文に置き換えるだけである。 ところが、単語の種類は文字に比べてはるかに多いため、単純にhot-one方式でベクトルに対応させるのは甚だ効率が悪い。 そこで、いくつかの工夫を凝らした手法が開発され、ライブラリとして手軽に利用できるようになっている。

ここでは、トピック分析用のライブラリとしてよく知られている gensim の機能を使って、単語のベクトル化を行ってみよう。

# coding:utf-8

import sys
import re
from gensim.models.word2vec import Word2Vec

path='ulysses.txt'

ndim=200
window=20

punc='(\.|\:|\;|\!|\?|\n\n|--)'

with open(path,mode='r',encoding='utf-8') as f:
    raw_data = f.read()

sentences = re.split(punc,raw_data.replace('\n',''))

training_data=[ ]

for s in sentences:
    s = s.replace(',','')
    s = s.strip()
    s = s.upper()
    if len(s)>0 and re.fullmatch(punc,s)==None:
        wlist = re.split(r'\s+',s)
        training_data.append(wlist)
        
w2v_model = Word2Vec(training_data, size=ndim, min_count=2, window=window)

w2v_model.save('word2vec-ulysses.model')

上記のコードを動かすと、ulysses.txtのデータを文の単位に分解し、さらにそれらの文を単語に分解することで

[ ['HE', 'SAID', 'STERNLY'], ['HE', 'ADDED', 'IN', 'A', "PREACHER'S", 'TONE'], ...]

のようなリストのリストが生成される（training_data）。

これを、Word2Vecモジュールに与えると、指定した次元の単語ベクトルのモデルが生成される。 ここで、size=.. は単語ベクトルの次元、min_count=.. はここで指定された回数以上登場した単語のみを対象とするための指定、 window=.. は、前後、いくつの単語までを考慮するか、をそれぞれ表す。

単語ベクトルの演算

生成した単語モデルを呼び出して、'LOVE'の単語ベクトルに近いベクトルを持つ単語を10個表示するコードの例を以下に示す。

# coding:utf-8

import re
import numpy as np
from gensim.models.word2vec import Word2Vec

w2v_model = Word2Vec.load("word2vec-ulysses.model")

ndim=w2v_model.vector_size

vec = w2v_model.wv['LOVE'] 

sampled_word = w2v_model.wv.most_similar( [ vec ], [], 10)

print(sampled_word)

[('LOVE', 1.0), ("SHE'S", 0.9842973947525024), ('NAUGHTY', 0.9798166751861572), ('WISH', 0.9783136248588562), 
 ('PLEASE', 0.9782708287239075), ('SOUL', 0.9780334234237671), ('MEET', 0.977763295173645), ('THINKS', 0.9777297973632812), 
 ('PERFUME', 0.9767372608184814), ('LIKES', 0.9763315916061401)]

語と共に表示される数値は、ベクトル同士の方位角の近さ（コサイン距離）を表しており、同じ向きのベクトルでは1（最大値）、直交する方向(「無関係」に対応)では 0 となる。 リストを見るとLOVEと意味的に近いと思われる単語が多いことに気づく。

上記のコードを少し変更して、'MUSIC'と'ROOM'のベクトルの和を求め、それに近い単語を出力してみる。

vec =    w2v_model.wv['MUSIC'] + w2v_model.wv['ROOM']
sampled_word = w2v_model.wv.most_similar( [ vec ], [], 10)
print(sampled_word)

すると、部屋の中で音楽が奏でられているような状況に関係する単語がいくつか抽出される：

[('STAGE', 0.9973996877670288), ('TOBE', 0.9968059659004211), ('PARTY', 0.9965268969535828), ('GAME', 0.9954688549041748), 
('SHAPE', 0.9952409267425537), ('HECOULD', 0.9950450658798218), ('SENDING', 0.9950354099273682), 
('NAKED', 0.9946911334991455), ('FALSE', 0.9946339726448059), ('SIZE', 0.9946198463439941)]

このように、単語ベクトル同士の演算によって、語の意味の操作がある程度可能になる。

単語ベクトルは、共起性（文中の近い場所に現れているかどうかの程度）によって決められるため、 意味が「反対」の語（反意語）のベクトルが必ずしも反対方向を向くわけではなく、むしろ、同類の語として分類される可能性がある点には注意が必要である。

　練習：単語ベクトルモデルの生成

著作権上、使用が問題の無いテキストファイルを見つけ、単語ベクトルモデルを生成し、上記の説明に倣って、動作を確認してみなさい。