Pythonプログラミング（リカレントネットワーク）

(このページは書きかけ)

系列情報の生成と学習を行うリカレントネットワーク

時系列的なベクトル情報（状態）$\boldsymbol{y}(t)$を考える。ここで、時刻$t$は離散的（$t=0,1,2,\cdots$)とする。つまり$t$番目の情報が$\boldsymbol{y}(t)$ということである。 加えて、$t$番目に別のベクトル情報$\boldsymbol{x}(t)$が提示されるような状況を考える。 そのとき、$t+1$番目の状態が、$t$番目の状態によって決まる、すなわち、ベクトルからベクトルへの変換 $$ \boldsymbol{y}(t+1) = f(\boldsymbol{y}(t),\boldsymbol{x}(t)) \tag{1} $$ 関係が与えられているとしよう。 この関係を図示すると

のようになり、次の時刻のデータを再び入力に戻すような再帰（リカレント）的な状況になっていることがわかる。 ここでの$f$をニューラルネットで構成したのがリカレントニューラルネット(RNN)である。 RNNは様々な系列情報（単語の系列（文章や会話）、経済指標などの時系列、等々）の処理に広く用いられている。

ここで、自然な着想として、$f$ の部分をフィードフォワード型のネットワークで構成してみたくなる。 ところが、自分自身へのリターンがあることから、0ステップ目を出発点とすると、$\boldsymbol{y}$ の「それまで」の系列 $$ \{ \boldsymbol{y}(t), \boldsymbol{y}(t-1), \cdots, \boldsymbol{y}(1),\boldsymbol{y}(0) \} $$ に依存して次の状態が決まることに気づくであろう。つまり、1式は $$ \boldsymbol{y}(t+1) = f(\{ \boldsymbol{y}(t), \boldsymbol{y}(t-1), \cdots, \boldsymbol{y}(1),\boldsymbol{y}(0) \},\boldsymbol{x}(t)) $$ のような構造になっている。

これを層状のニューラルネットで表現しようとすると、実質的に層の数が膨大に（無限に「深い」ネットワークに）なってしまう。 そのため、RNNで長時間の系列情報を学習させることは原理的に難しいとされてきた。

系列情報処理に適したアーキテクチャ

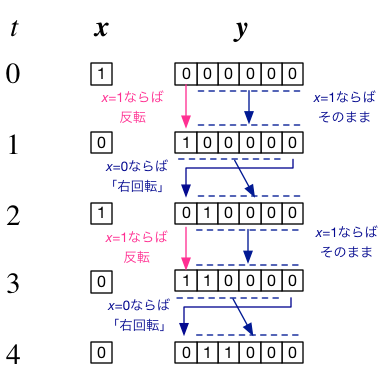
ここで、１ステップだけ時間が更新されると、$\boldsymbol{y}$の内容が「右シフト（右巡回）」するような系列情報を考えてみよう。 例えば、$\boldsymbol{y}(t)=(1,0,1,0,0,0)$ ならば $\boldsymbol{y}(t+1)=(0,1,0,1,0,0)$ といった具合である。 いちばん左端の桁には、一番右側の桁が入ることにする。

ただし、もし$x = (1)$ ならばシフトは行わず、$\boldsymbol{y}$の左端の桁のみが反転する（0ならば1に、1ならば0変化する）、 といった具合に、$x$によって挙動が切り替わるようにしてみよう。

もしも入力が$x=(0)$であれば、最初の$\boldsymbol{y}$の状態が6ステップ周期で繰り返されるので、 これは繰り返しパターンを記憶したり・生成したりできる装置とみなせる。 また、$x=(1)$よって、そのパターンを書き換えることも可能となる。

そして、こうした動作を可能にするための機械（あるいは論理回路）を設計しようとしたら、候補のひとつとして、以下のような構成が考えられるだろう：

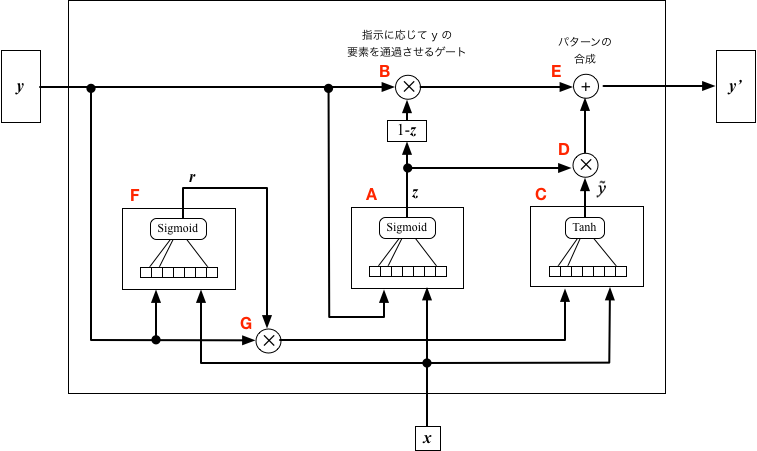
図で、Aのブロックは、$x$の状態によって、$\boldsymbol{y}$のどの「桁」を更新すべきかを出力する。$x=(1)$ならば $(1,0,0,0,0,0)$、 $x=(0)$ならば $(1,1,1,1,1,1)$ のように、更新されるべき箇所のみを1とおく。 これをゲート信号と呼ぶ。

Bのゲートでは、ゲート信号の「否定(negate)」と$\boldsymbol{y}$の要素ごとの積を取る。 ゲート信号が $(1,0,0,0,0,0)$で$\boldsymbol{y}=(y_1,y_2,y_3,y_4,y_5,y_6)$とすれば、 $(0,y_2,y_3,y_4,y_5,y_6)$が出力される。 もし、ゲート信号が $(1,1,1,1,1,1)$ならば、Bの出力は $(0,0,0,0,0,0)$ となる。 つまり、ゲートは$\boldsymbol{y}$のうち、そのまま保持すべき部分のみを切り取る働きをする。

Cのブロックでは、$x=(0)$ならば$\boldsymbol{y}$を右回転した結果を出力する。 例えば、$\boldsymbol{y}=(1,0,1,0,1,0)$であれば、出力は$(0,1,0,1,0,1)$である。 一方、$x=(1)$ならば、$\boldsymbol{y}$のビットを反転して出力する。

Dのゲートでは、ゲート信号と、Cブロックの出力の要素毎の積を取る。 $x=(1)$の場合は、ゲート信号が$(1,0,0,0,0,0)$で、これとCブロックの出力との積を取るのだから、いちばん左以外の桁を「落とす」ことになる。 $x=(0)$の場合、すなわちゲート信号が$(1,1,1,1,1,1)$ならば、Cブロックの出力は全て「透過」する。

そして、最後にEで、２つの信号が統合（加算）され、次の状態として出力される。

以上では、$\boldsymbol{y}$のパターンの「右回転」動作を$\boldsymbol{x}$で操作するという、 かなり特殊な例について考えたが、AブロックとCブロックの入出力関係を調整することで、他のいろいろなケースにも 対応できるようになるはずだ。 そのためには、A, Cをニューラルネットで構成して、手本となる系列パターンを学習させればよい。

ゲート付きのリカレントネット(GRU)

前節の例のように、ゲートを用いて、状態ベクトル（$\boldsymbol{y}$)のうちで、繰り越す部分と 更新すべき部分を選り分け、更新すべき部分のみを状態（$\boldsymbol{y}$)と入力（$\boldsymbol{y}$）に応じて生成することによって、 過去の記憶を残しつつも、状況変化にも対応できるようなニューラルネットを構成できるようになる。

こうした発想に基づいて設計されたニューラルネットとしては、LSTM(Long Short-Term Memory）や GRU(Gated Recurrent Unit)が知られている。 そして、LSTMやGRUを使うことによって、長期にわたる系列情報が可能となり、それを使うことで、例えば、機械翻訳の精度が格段に向上した。 ここでは、GRUに限って、その構造を見ていくことにする。

前節の例で示した「論理回路」とGRUの主な違いをまとめると、

1. 前節では、状態ベクトル$\boldsymbol{y}$の各要素は0または1を取り得るとしたが、GRUではこれを $\pm 1$ の間の連続値とする。 一方、ゲート信号の各要素についてあ 0から1の連続値を許すことにする。そして、繰越情報と更新情報を連続的にブレンドする。
2. パターンを生成するA, Cブロックをニューラルネットで構成する。Aの出力はシグモイド関数（出力は0から1の範囲）、 Cの活性化関数はここではtanh関数（出力は-1から1の範囲）とする（ただし、他の微分可能な関数でも構わない）。
3. Cブロックに入力する状態ベクトル$\boldsymbol{y}$をゲートで制限する（下図のF,G）。

以下の式中では、ベクトル $\boldsymbol{x} = (x_1, \cdots, x_m)$と$\boldsymbol{y} = (y_1, \cdots, y_n)$の要素を並べて生成したベクトルを $$ \boldsymbol{x} \oplus \boldsymbol{y} = (x_1, \cdots, x_m, y_1, \cdots, y_n) $$ と表記することにする。 また、Aブロックの荷重ベクトルを $$ W^z = (W^z_1, \cdots, W^z_{m+n}) \\ $$ 等と表記する（他のブロックも同様）。 シグモイド関数を$\sigma ()$で表現することにすると、GRUにおいて、Aブロックの入出力関係は $$ \boldsymbol{z}(t) = \sigma\left(W^z \cdot (\boldsymbol{x}(t) \oplus \boldsymbol{y}(t) ) \right) \\ $$ Fブロックは $$ \boldsymbol{r}(t) = \sigma\left(W^r \cdot (\boldsymbol{x}(t) \oplus \boldsymbol{y}(t) ) \right) \\ $$ となる。 また、Aブロックでの更新ルールは $$ \boldsymbol{\tilde{y}}(t) = \tanh\left(W \cdot [\boldsymbol{x}(t) \oplus \{ \boldsymbol{r}(t) \otimes \boldsymbol{y}(t)\} ] \right) \\ $$ とする。そして、最終的なユニットの出力は、$\boldsymbol{y}(t)$ と $\boldsymbol{\tilde{y}}(t)$ の要素毎の平均、すなわち $$ \boldsymbol{y}(t+1) = (\boldsymbol{1} - \boldsymbol{z}(t)) \otimes \boldsymbol{y}(t) + \boldsymbol{z}(t) \otimes \boldsymbol{\tilde{y}}(t) $$ とする。 ここで $\boldsymbol{1} = (1,1, \cdots, 1)$である。

GRUによる系列予測

GRUは典型的なリカレントネットワーク構造のひとつとみなされており、ほとんどのフレームワークでサポートされている。 ここでは、Kerasを使って、GRUを用いたニューラルネットに時系列を学習させ、初期値のみを与えてその後を予測させる実験をしてみよう。

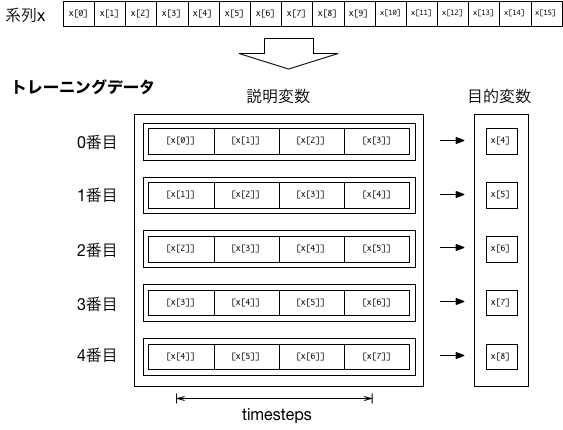
配列 x[i] に系列データが格納されているとしよう。 例えば、4ステップ分の情報から1ステップ先を予測できるよう学習させるには、 以下の図のようにトレーニングデータ（説明変数と目的変数の組）を準備すればよい。

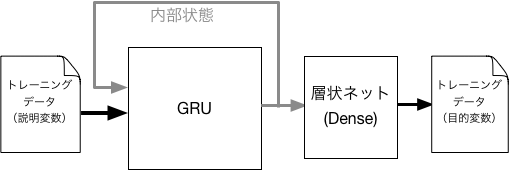
そして、以下のような構造のモデルを構成し、入力（説明変数）に対応した出力（目的変数）が得られるように、トレーニングさせる。 ここで、GRUの内部状態を、得たい出力に変換するため、GRUの出力にさらに層状ネットワークを接続する。

この方法で、実数の系列を学習させ、学習後に、実際のデータと予測値をプロットするコードの例を以下に示す。

このコードでは、「複雑な」関数 $$ v(t) = \left(1 + \cos(1.5 t)/2 \right) \sin\left( t + \sin(2.1 t)/2 \right) $$ を使って実数の系列を発生させ、配列xdata[ ]に保存し、それを元に、トレーニング用データを作成している。 timestepは24であるので、24ステップ分のデータからその次を予測することになる。

ネットワークモデルの構成は

from keras.models import Sequential
from keras.layers import Dense,GRU

model = Sequential()
model.add(GRU(64, input_shape=(timestep,1),use_bias=True))
model.add(Dense(1, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='Adam')

のみで事足りる。

GRU(内部変数の要素数,...)でGRUの内部変数（前節の$\boldsymbol{y}$）の要素数を、 input_shape=(タイムステップ幅, 説明変数の数)で、入力（前節の$\boldsymbol{x}$）の要素数を、それぞれ設定する。

予測する変数の数は1なので、Dense(1, ...)で、素子数を1に設定している。 また、結果は任意の範囲の実数値をとり得るため、activation='linear'を指定した。

# coding: utf-8
from keras.models import Sequential
from keras.layers import Dense,GRU
import numpy as np
import math
import matplotlib.pyplot as plt

# 系列データの生成
xdata=[]
tdata=[]
for t in np.arange(0,20*math.pi,0.1):
    v = (1.0 + 0.5*math.cos(t*1.5))*(math.sin(t + 0.5*math.cos(2.1*t)))
    xdata.append([v])
    tdata.append(t)

# トレーニングデータの生成
timestep=24

x_train = [ ]
y_train = [ ]

for i in range(len(xdata) - timestep ):
    x = xdata[i: i + timestep]
    y = xdata[i + timestep][0]
    x_train.append(x)
    y_train.append(y)

x_train = np.array(x_train, dtype=np.float32)
y_train = np.array(y_train, dtype=np.float32)

# モデルの生成
model = Sequential()
model.add(GRU(64, input_shape=(timestep,1),use_bias=True))
model.add(Dense(1, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='Adam')
model.summary()

# 学習
model.fit(x_train, y_train, epochs=100, batch_size=32)

# 学習結果を使った「予測」
taxis=[]
y0=[]
y1=[]
first_time=True

for i in range(200):
    if i>=len(xdata)-timestep:
        break
    if first_time:
        x = np.array(xdata[i: i + timestep])
        first_time=False
    else:
        x=np.roll(x,-1)
        x[-1]=y_predict
    
    xin= np.array([x], dtype=np.float32)    
    y_predict = model.predict(xin)[0][0]
    y_train = xdata[i + timestep][0]
    taxis.append(tdata[i+timestep])
    y0.append(y_train)
    y1.append(y_predict)

# 結果のプロット
plt.plot(taxis,y0, color=(1.0,0,0.0), linewidth=1.0)
plt.plot(taxis,y1, color=(0.0,1.0,1.0), linewidth=1.0)
plt.xlabel('t')
plt.grid(True)
plt.show()

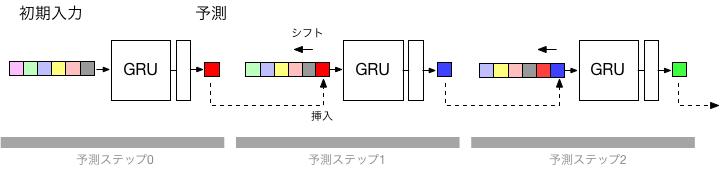
学習が完了後、まず初期値を入力し、その結果を次のステップの予測のための入力とする操作を繰り返すことによって、多段階先までの予測が可能となる（下図）。

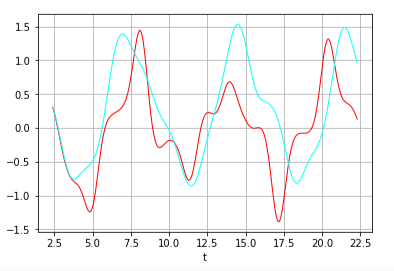
以下が、最初のtimestep(25ステップ)分のデータをまず与え、その後の値を順繰りに予測させて結果である（赤がトレーニングデータ、水色が予測出力）。 timesteps程度までの未来はほぼ正確に予測できているが、その後は、次第にずれが顕著になっている様子が判る。

　練習：パラメータの予測精度への影響

上のサンプルコードで、timestepの値、GRUの内部素子数、トレーニング回数（epochs=反復回数, batch_size=バッチサイズ）等を調整し、 予測精度への影響を調べてみなさい。