Pythonプログラミング（画像の分類）

Pythonプログラミング（ディープラーニングによる画像の分類・入門編）

(このページは書きかけ)

視覚情報処理の多段階的な構造

画像($\boldsymbol{x}$)を与えると、その画像のカテゴリー($c$)を判別してくれるニューラルネット $$ c = g(\boldsymbol{x}) $$ のデザインを考えてみよう。「イヌ」の画像を与えると「イヌ」を、「ネコ」の画像を与えると「ネコ」、と分類するような機械を設計しようということである。の入力情報に画像を層状のフィードフォワード・ニューラルネットに入力し、出力には必要なカテゴリーの数だけの素子を用意すれば、原理的には、これを実現することができそうである。しかしながら、やみくもに木材を継いでいっても家は建たないように、基本的な構造設計（アーキテクチャ）無しでは、実際にそれを動作させるのは困難である。

多年に渡る脳や神経科学の多年にわたる研究によって、視覚情報が脳でどのように処理されているかが、徐々に明らかにされつつある。ここでは、ネコやサルなどの高等動物を前提に、その概要をみておこう。脳は皮質と呼ばれるシート状の構造をしており、シートには6つの層が確認されている。その大きなシートは機能単位ごとに区分けされており、そのひとつに視覚野がある。網膜に入った光の信号は、ニューロンの電気信号に変換されて、視覚野に伝送される。視覚野はさらにいくつもの階層に分かれていて、V1,V2,V3,V4,V5 等々の名前が付けられている。網膜の情報はまずV1に入り、そこで処理された情報がV2、次いでV3に・・、といった風に、段階的に情報が伝達される。実際の脳では、単純なバケツリレー式ではなくて、逆方向に遡上したり、バイパスしたりする経路もあるようだが、大まかな情報の流れは、一方向的と考えて良さそうである。

V1には網膜の視覚情報が直接的に投影されているが、網膜細胞の信号がそのまま「ピクセル情報」として扱われるわけではなく、小領域ごとに処理・加工されていることがわかっている。つまり、網膜上の位置を二次元的に$(i,j)$と表記するとすると、その点の比較的近傍の画像情報も使いながら、 $(i,j)$の辺りで画像が「縦線」か「斜め線」か、あるいは「横線」か、などといった具合に、特徴の抽出が行われている。そして、シート状の皮質には、部分画像の特徴に反応する非常に小さな区画（カラムと呼ばれている）が配列していることがわかっている。より後段になると、比較的大きな単位の図形や、あるいは運動の方向などに選択的に反応するカラムが存在することも確かめられている。

こうして処理が進んだ情報は、連合野と呼ばれる領域に送り込まれ、他の情報と統合されながら諸々の高度な（知的な）プロセスを経て、運動野に司令が送られる。そして、視覚情報を含む様々な感覚情報に基づいて、我々の行動が決まるというわけである。

画像特徴への選択的な反応

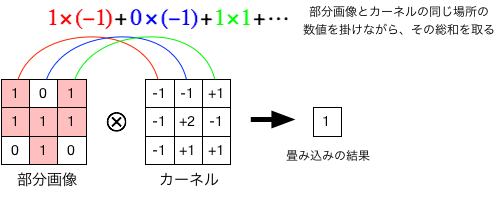
ここで、$3 \times 3$の画像を考え、それに畳み込み（convolution)と呼ばれる操作を施してみよう。その操作はいたって簡単で、カーネルと呼ばれる同じサイズの配列を用意し、そこに数値を並べておいて、同じ場所の数値同士を掛け合わせながら総和を取るだけである（下図）。

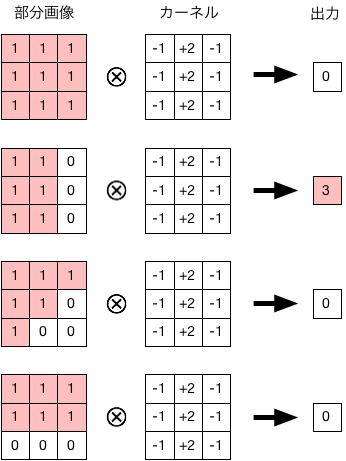
ここで、カーネルの数値の並びを工夫することで、特定の特徴を持った画像に選択的に反応できるようにすることができる。例えば、縦方向の画像の「エッジ」を検出する例を以下に示す。

大脳皮質の各カラムが担っている機能からも連想されるように、抽出したい特徴に合うおうにカーネルをうまく調整すれば、画像を識別する能力が向上するはずである。そして、ニューラルネットの学習過程で、カーネルの値（ニューラルネットの荷重に対応）が「適切に」調整されることが期待できる。

Kerasには、画像（２次元情報）の畳み込みを行うための構造があらかじめ用意されており

from keras import models	
from keras.layers import Conv2D
	
model=models.Sequential()
model.add(Conv2D(32,(3,3),activation="relu",input_shape=(128,128,3)))
...

のようにConv2Dレイヤーを追加すればよい。ここで、最初の引数は用いるカーネルの種類の数である。上の例では最大32通りやり方で特徴を識別できることになる。次の引数（タプル）は、部分画像の大きさで、上の例では $3 \times 3$ のサイズとなる。

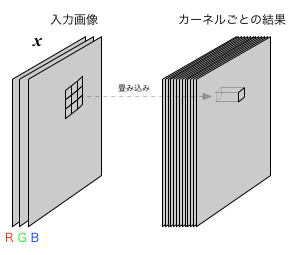
この節の畳み込みの説明ではモノクロ画像を仮定したが、カラー画像を扱う場合には、R,G,Bのそれぞれについて濃淡情報が入力される。その場合の畳み込み操作は、$3 \times 3$の部分画像を用いる場合、$3 \times 3 \times 3$個のデータについて積和を計算することになる。

情報を縮減する

多層のネットワークを構成する際に、近傍の複数の値の代表値のみを次に伝達するようにすれば、記憶容量や計算コストを大きく節約することができる。この手法はプーリング（pooling）と呼ばれ、たとえば、$2 \times 2$の部分画像をピクセルと見なせば、データのサイズを1/4にすることができる。その際、縮減後のピクセル値を決めるやり方として、最も輝度の大きな値を取り出す（max pooling)、平均値を使う(average pooling）等が一般的である。

KerasでPooling層を加えるには

from keras import models	
from keras.layers import Conv2D, MaxPooling2D
	
model=models.Sequential()
model.add(Conv2D(32,(3,3),activation="relu",input_shape=(128,128,3)))
model.add(MaxPooling2D((2,2))
...

のようにMaxPooling2D レイヤー、あるいはAveragePooling2Dレイヤーを加えればよい。

CNNを構成する

畳み込み層とPooling層を「積み上げて」いくことによって、入力に近い層ではプリミティブな特徴に選択的に反応していたものが、後段になるにしたがって、次第に高次の特徴（全体的な様子）に選択的に応答するようになると期待できる。ここで、期待できる、と書いたのは、その辺りの理論的な裏付けはまだはっきりしていないからである。

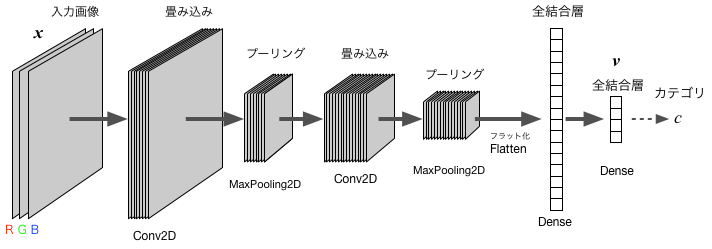
多くの場合にうまくいく構造（アーキテクチャ）として、以下のような畳み込みニューラルネット（Convolutional Neural Network; CNN）が提案され、実用的に各所で使われている。その代表的な例を以下に図示した。層の数や素子数、カーネル（フィルター）の数などは、問題に応じて、適宜調整する必要がある。

上の例で示したCNNをKerasで記述すると、以下のようになる：

from keras import models
from keras.layers import Conv2D,MaxPooling2D,Flatten,Dense

model=models.Sequential()
model.add(Conv2D(8,(3,3),activation="relu",input_shape=(128,128,3)))
model.add(MaxPooling2D((2,2))
model.add(Conv2D(16,(3,3),activation="relu")
model.add(MaxPooling2D((2,2))
model.add(Flatten())
model.add(Dense(16,activation="relu"))
model.add(Dense(4,activation="softmax"))

ネットワークの前段部分（Conv2Dレイヤ、MaxPooling2Dレイヤ）では、二次元的なデータ配列がカーネルの数だけ積み重なったデータ構造が保持される（各素子の位置関係が保持されている）一方で、後段の全結合型のレイヤでは、全ての素子は一様（フラット）である。そこで、こうした構造の違いを変換するため、両者の間にFlattenレイヤを設けている（Flattenレイヤが無いと、データの構造のミスマッチによってエラーとなる）。

過学習を防ぐために、学習の過程で実際に更新につかう結合制限する手法が有効である(dropoutと呼ばれる）。以下はDropoutレイヤを追加した例である：

from keras import models
from keras.layers import Conv2D,MaxPooling2D,Flatten,Dropout,Dense

model=models.Sequential()
model.add(Conv2D(8,(3,3),activation="relu",input_shape=(128,128,3)))
model.add(MaxPooling2D((2,2))
model.add(Conv2D(16,(3,3),activation="relu")
model.add(MaxPooling2D((2,2))
model.add(Dropout(0.5)
model.add(Flatten())
model.add(Dense(16,activation="relu"))
model.add(Dropout(0.5)
model.add(Dense(4,activation="softmax"))