Pythonプログラミング(層状ネットワークによる確率分布の学習)
(このページは目下作成中)
確率的な挙動の学習
2つの確率変数$X$,$Y$を考えて、その結合確率分布を$P(x,y)$とする。さらに、別の確率分布$Q(x,y)$を考えたとき、2つの確率分布の違いの程度を表す指標として カルバック・ライブラー情報量(Kullback–Leibler divergence) $$ D = \sum_{x,y} P(x,y) \log \left( \frac{P(x,y)}{Q(x,y)} \right) $$ が用いられている。 $x,y$が連続的な場合は $$ D = \int dx \int dy P(x,y) \log \left( \frac{P(x,y)}{Q(x,y)} \right) $$ と考えればよい。 不可解な定義のように目に映るかもしれないが、$D \ge 0$であり、等号は2つの分布が完全に一致する場合($P(x,y)=Q(x,y)$)に成り立つなど、 分布の間のある種の「距離」を定義する量になっていることが判る。
以下では、$Q(X,Y)$がニューラルネットの挙動を、$P(X,Y)$をトレーニングデータの性質を表すと見なすことにしよう。 KL情報量を、 $$ D = - \sum_{x,y} P(x,y) \log Q(x,y) + \sum_{x,y} P(x,y) \log P(x,y) $$ を書き直すと、右辺第二項の$P(X,Y)$のエントロピーは、データセットを決めれば定数とみなせる。 とすると、ニューラルネットがトレーニングデータの性質をなるだけ忠実に再現するためには クロスエントロピー $$ C = - \sum_{x,y} P(x,y) \log Q(x,y) $$ を最小化するように、ニューラルネットのパラメータ(構造や荷重等)を調整すればよい、ということになる。
$X$に対して$Y$が一意に決まる場合:関数の学習
$X$を与えると、関数関係$y=g(x)$によって$Y$が一意に決まるような場合、条件付き確率はデルタ関数を使って形式的に $$ P(y|x) = \delta(y-g(x)) $$ と表すことができる($x$と$y=g(x)$が必ずペアで出現し、それ以外の可能性はゼロ)。 そのとき、$p(x,y) = p(y|x) p(x)$を思い出すと、クロスエントロピーは $$ C = - \frac{1}{Z} \int dx dy \, \delta(y-g(x)) p(x) \log Q(x,y) = - \int dx \, p(x) \log Q(x,g(x)) $$ となる。$x$を与えたときのニューラルネットの出力を$f(x)$としたとき、このネットワークが$y$を出力する確率分布がガウス分布 $$ Q(x,y) \propto \exp\left(- \beta (y - f(x))^2\right) $$ で表現できるとすれば、上記のクロスエントロピーは $$ C \propto \int dx \, p(x) \left( g(x) - f(x) \right)^2 $$ すなわち、$C$の最小化は、事前確率 $p(x)$ で重み付けられた教師信号と出力信号の自乗誤差の最小化とみなすことができる。
離散的な事象の場合:パターンの分類
ここで、$X$と$Y$が対になって発生するような離散的な事象を考えてみる。 例えば、$X$がセンサーに入力した画像、$Y$が対象物の名前(「イヌ」、「ネコ」、等々)であるとしよう。 そして、$P(x,y)$は正解(トレーニング用のデータセット)に対する確率分布、 $Q(x,y)$はニューラルネットの確率分布とする。
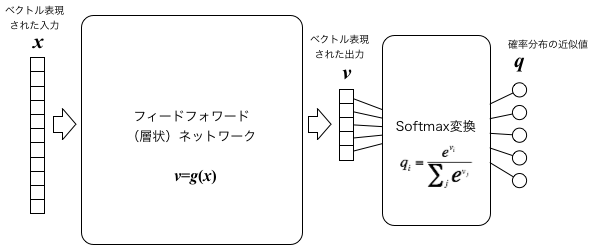
ここで、ネットワークにちょっとした工夫を施してみる。 すなわち、$Y$が$m$個の事象から成るとして、 $i$番目(ただし、$1 \le i \le m$)のニューロンの出力 $q_i$ が、$X$という条件下で$Y$の$i$番目の事象が起こる確率 $Q(Y_i | X)$ とみなせるように、 ニューラルネットを構成する。
具体的には、層状ネットワークに$m$個の出力素子を設ける。$x$を入力した際の$i$番目の出力を$v_i$とすると、 $$ q_i = \frac{e^{v_i}}{\sum_{j=1} e^{v_j}} $$ (これはSoftmax変換と呼ばれる)とおいて、この$q_i$を$Q(Y_i | X)$ と見なすのである。定義から、 $$ \sum_{i=1}^m Q(Y_i | X) = 1 $$ は自動的に満足されている。
$x$の事前確率は「共通」であることを考慮すると、クロスエントロピーは $$ \begin{eqnarray} C & = & - \sum_x P(x) \sum_j P(Y_j|x) \log\left( q_j P(x) \right) \\ & = & - \sum_x P(x) \sum_j P(Y_j|x) \left\{ v_j - \log\left(\sum_{\ell} e^{v_\ell}\right) \right\} - \sum_x P(x) \log P(x) \sum_j P(Y_j|x) \end{eqnarray} $$ となるが、ネットワークのパラメータに依存するのは、最初の項のみだから、これを改めて $$ \begin{eqnarray} C' & = & \sum_x P(x) \sum_j P(Y_j|x) \left\{ v_j - \log\left(\sum_{\ell} e^{v_\ell}\right) \right\} \\ & = & \sum_x P(x) \left\{ \sum_j P(Y_j|x) \, v_j - \log\left(\sum_{\ell} e^{v_\ell}\right) \right\} \end{eqnarray} $$ とおいて、$C'$を最小化すればよい。
$v_j$がパラメータ$\theta$に依存しているいるとすると、$C'$の勾配が $$ \frac{\partial C'}{\partial \theta} = \sum_x P(x) \sum_j \left\{ (P(Y_j|x) - q_j) \frac{\partial v_j}{\partial \theta} \right\} $$ で評価できるから、「教師信号」とネットワークの出力の差($P(Y_j|x) - q_j$)と 勾配$\frac{\partial v_j}{\partial \theta}$の積に応じて$\theta$を更新すれば良い。
ここで、 $$ \begin{eqnarray} \frac{\partial}{\partial \theta} \log\left(\sum_{j} e^{v_j}\right) = \frac{1}{\sum_{\ell} e^{v_\ell}} \frac{\partial \sum_{j} e^{v_j}}{\partial \theta} \\ = \sum_j \frac{e^{v_j}}{\sum_{\ell} e^{v_\ell}} \frac{\partial v_j}{\partial \theta} = \sum_j q_j \frac{\partial v_j}{\partial \theta} \end{eqnarray} $$ という変形を行った。
ニューラルネットによる確率予測
以上を踏まえると、ベクトル表現された$k$番目のパターン$\boldsymbol{x}^k=(x^k_1, \cdots, x^k_N)$と、それに対応する出力$y^k$が$j$番目のカテゴリーに属する確率 $q(\boldsymbol{x}^k,y^k=j)$ を出力するニューラルネットを、以下の図のように、設計することができる。
『サザエさんじゃんけん研究所公式ウェブサイト』の主宰者様からデータの使用について許可をいただきました。 ここに記して感謝いたします。
唐突ではあるが、ここで、ジャンケンを例に考えてみよう。国民的なアニメで番組の終わり頃に毎週主人公が出す「グー(rock)」、「パー(paper)」、「チョキ(scissors)」 をまとめたサイト『サザエさんじゃんけん研究所公式ウェブサイト』から、 1991年からの放送分の時系列をまとめたデータをこちらに用意した。 ファイルの内容は
1 SCISSORS 2 ROCK 3 ROCK 4 PAPER 5 SCISSORS 6 ROCK ...
のように、何回目の放送か、と、その回のジャンケンの手が、各行に書かれている。
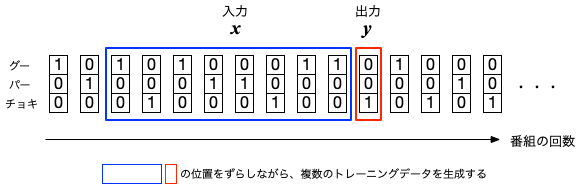
これを元に、NumPyの配列を使って「グー」を [1,0,0]、「パー」を[0,1,0]、チョキを[0,0,1]と表現し直し、
8週分のデータを1セットにしたものを入力データ$x$とする。例えば、
[ [0,1,0], # パー [0,0,1], # チョキ [0,0,1], # チョキ [1,0,0], # グー [0,1,0], # パー [1,0,0], # グー [0,0,1], # チョキ [0,1,0] # パー ]
といった具合である。
一方、出力$y$に対応するのは、その翌週に出された手とする(下図参照)。
そして、ネットワークは、確率$P(x,y)$を近似するような出力が得られるようにデザインし、 結果は、NumPyの配列で
[0.6324105, 0.09085906, 0.27673042]
のように表現することにしよう。この場合、「グー」の確率が0.632..、「パー」が0.090...、といった具合である。
このようなアイデアに従って、実際のデータを使って確率分布を学習するPythonコードの例を以下に示す:
# coding: utf-8
from keras import layers,models
from keras import optimizers
from keras.utils import np_utils
import numpy as np
with open('sazae-san-rps.txt') as f:
data = f.readlines()
seq=np.empty((0,3), float)
for line in data:
w = line.split()
if w[1]=='ROCK':
rps = [1,0,0]
elif w[1]=='PAPER':
rps = [0,1,0]
else:
rps = [0,0,1]
seq = np.append(seq,np.array([rps]),axis=0)
x_train=[]
y_train=[]
x_test=[]
y_test=[]
len = seq.shape[0]
for i in range(len):
if i>=8:
x = seq[i-8:i,:]
y = seq[i,:]
if np.random.uniform() < 0.25:
x_test.append(x)
y_test.append(y)
else:
x_train.append(x)
y_train.append(y)
x_train = np.array(x_train,dtype=np.float32)
y_train = np.array(y_train,dtype=np.float32)
x_test = np.array(x_test,dtype=np.float32)
y_test = np.array(y_test,dtype=np.float32)
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(8,3)))
model.add(layers.Flatten())
model.add(layers.Dense(512,activation='relu'))
model.add(layers.Dense(3,activation='softmax'))
model.compile(loss='kullback_leibler_divergence',optimizer='rmsprop',metrics=['acc'])
model.fit(x_train,y_train,epochs=100,batch_size=10, validation_data=(x_test,y_test))
json_string=model.to_json()
with open("train.json","w") as f:
f.write(json_string)
model.save_weights("train.hdf5")
実行にあたり、コードと同じディレクトリ(フォルダ)に、データファイルsazae-san-rps.txtを置いておく必要がある。
正常に動作すると、ネットワーク構造が train.json、学習結果(荷重)が train.hdf5 というファイル名で保存され、終了する。
こうしておくことで、デザインしたネットワークと、学習の結果を、これらのファイルを読み込んで何度でも再利用することができる。
以下のコードは、実際に、学習済みデータを使って、8週分のデータから、次の週の手を予測する例である:
from keras import models
from keras.models import model_from_json
import numpy as np
model=model_from_json(open("train.json").read())
model.load_weights("train.hdf5")
x=np.array([[
[0,1,0], # パー
[0,0,1], # チョキ
[0,0,1], # チョキ
[1,0,0], # グー
[0,1,0], # パー
[1,0,0], # グー
[0,0,1], # チョキ
[0,1,0] # パー
]],float)
f=model.predict(x)
r=f[0]
print(r)
モデルが扱う情報の次元とデータ数
上の例では、8週分のデータ($\boldsymbol{x}$)とその翌週($y$)、合わせて9週分のジャンケンの手の組み合わせに対する確率分布を学習・予想した。 このとき、可能な状態の数は $3^9 = 19683$通り、ということになる。もし、$n$週まで遡ることにすれば、状態数は$3^{n+1}$となり、$n$に対して指数関数的に増加する。 それに対して、トレーニングに使えるデータの数は限られるので、$n$が大きなモデルを構成しても、それを学習させるに必要なデータを得ることは困難となってしまう (「次元の呪い(the curse of dimensionality)の一種)。
したがって、モデルの規模、入出力の次元は、入手できるデータの性質や規模に見合うように、検討しなけばならない。
 練習:条件付き確率のテーブルの作成
練習:条件付き確率のテーブルの作成
上記の例と同じデータ(sazae-san-rps.txt)を読み込み、 2週前分+「今週」のデータから、条件付き確率のテーブル($3 \times 3$)
P(今週の手|1週前の手,2週前の手)
を構成し、過去2週分の手を入力すると次の手の確率を出力するコードを作成してみなさい。