Pythonプログラミング（ニューラルネットの次元の拡張）

(このページは目下作成中)

入出力の数を増やす：多変数関数の学習

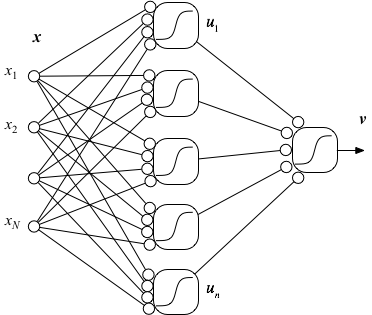
関数の近似を行うニューラルネットを、多変数関数 $y = f(x_1,x_2, \cdots, x_N)$版に拡張するのは容易で、 構造的には、入力段に複数の素子を並べて接続するだけである。 また、学習のアルゴリズムも、その手間を除けば、1入力の場合と全く同様である。

さらに、出力の数を、$v_1, v_2, \cdots, v_N$と増やすことも同様に容易である：

このようにして、任意の次元のベクトル $\boldsymbol{x}$ を入力として、 ベクトル $\boldsymbol{y}$ 出力するような多変数関数 $$ \boldsymbol{y} = g(\boldsymbol{x}) $$ を学習するニューラルネット $$ \boldsymbol{v} = f(\boldsymbol{x}) $$ を構成することができる。

このとき、中間層の素子数$n$をいくらでも大きくすることができれば、「原理的には」$f$は$g$を任意の精度で近似できることがわかっている。 ここで「原理的には」と断ったのは、中間層の素子数が実用的な範囲に収まっているか、パラメータの調整がうまくできるか、といった点において、 実用性があるかどうかは、別の話しになるからである。

扱うデータの表現の拡大

入出力の素子数（次元）を拡大することによって、扱える情報の多様性も、当然ながら、増すことになる。

入力を二次元的に配列して、それぞれの値を「明るさ」に対応させれば、 画像情報のデータとみなすことができる。

入力のパターンを単語や文に割当て、例えば、(1,0,0,1)は「イヌ」、(0,1,0,1)は「ネコ」、(0,1,1,0)は「オウム」、(1,0,0,1)は「カワウソ」といった 風に解釈すれば、テキスト情報をデータ化したことになる。

この種の表現方法で最もシンプルなのは、素子のそれぞれに意味を割り当てるやり方である。 つまり、表現したい情報の種類の数だけ素子を並べておいて、$i$番目の素子が「オン」で、他がすべて「オフ」の場合に、 $i$番目のカテゴリーを表す、とするやり方である。 例えば、(1,0,0,0)が「犬」、(0,1,0,0)が「ネコ」、(0,0,1,0)が「オウム」、(0,0,0,1)は「カワウソ」といった具合である。 この方法は、カテゴリーの数だけ素子（脳科学の分野では「おばあさん細胞」と表現される）を用意しなければならないので、はなはだ効率が悪いが、 画像やパターンの認識や分類ではよく用いられる。

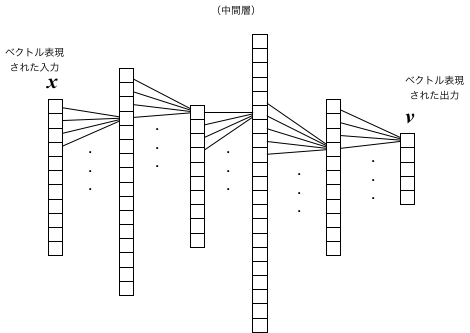
このように、各種の情報を値の組（一種の高次元ベクトル）としてデータ化する手法は、情報のベクトル表現と呼ばれ、 機械学習や人工知能の分野では一般的に使われている。

中間層の数を増やす：ディープニューラルネットワーク

フィードフォワード型の層状ニューラルネットに、処理対象の特性に合った中間層を「増築」し、 多層・多段の構造（アーキテクチャ）にしたものをディープニューラルネットと呼んでいる。 こうした発想は、第三次AIブームの以前にも、例えば、画像認識を行うニューラルネット「ネオコグニトロン」（福島邦彦） などの形で提案されていたが、実用的に使われるようになったのは近年になってからである。 中間層を増やすことで、目的に応じた柔軟な処理が可能となる一方で、パラメータ調整（学習）が困難であったが、 様々な改良のアイデアとハードウェア技術の進歩によって、実用的な段階に至った。

Kerasを使って層状のディープニューラルネットのモデルを構成するには、以下のように、mode.add(・・・)を継ぎ足していくだけで事足りる：

from keras.models import Sequential
from keras.layers import Dense, Dropout

...
	
model = Sequential()
model.add(Dense(24, input_dim=12, activation='sigmoid', use_bias=True)) # 1層目
model.add(Dense(48, activation='relu', use_bias=True))                  # 2層目
model.add(Dense(3, activation='sigmoid', use_bias=True, ))              # 3層目

入力を受け取る1層目は、入力ベクトルの次元を input_dim=12 のように指定しておく必要がある。 上の例の場合は、12要素からなるベクトル情報が入力されることになる。

画像のような二次元上に配列されたデータを入力する場合は、そこのところを、例えば、input_shape=(64,64) とすることで、 $64 \times 64$ ピクセルのグレースケール画像が取り込める。 色情報が必要な場合は、三原色それぞれの強度情報を得るため、input_shape=(64,64,3)とすればよい。

出力ベクトルの次元は、Dense(・・・)で設定する素子数そのものになる。上の例では3である。