Pythonプログラミング（ニューラルネットワークによる関数の学習）

(このページは目下作成中)

関数の「重ね合わせ」による近似

問題や事象をモデリングする際に、ある入力 $x$ に対して、出力 $y$ が対応するようなパターンに帰着できる例は極めて多い（殆どがそうである）。 例えば、$x$を入力画像とすると、$y$を「私の顔かどうか(yesなら$y=1$, noなら$y=0$」、といった具合に。

ここでは、最も簡単な例として、1変数の関数 $$ y = g(x) $$ によるモデリングから出発して考えてみたい。 ここで、関数$g$は問題毎の異なるし、単純な数学関数等では表せない可能性がある。 そこで、$g$を、性質のよく知れた簡単な関数の組み合わせによって近似する方法を考えてみる・

性質のよく知れた関数としては、例えば、シグモイド(sigmoid)関数 $$ f(u) = \frac{1}{1 + e^{-u}} $$ とか、（整流を伴う）ランプ（ReLU）関数 $$ f(u) = \left\{ \begin{array}{ll} 0 & u\lt 0 \\ u & \textrm{otherwise} \end{array} \right. $$ などがよく使われる。 この$f$は、もともと神経活動の活動度を表現するために導入されたことから、活性化関数と総称されている。

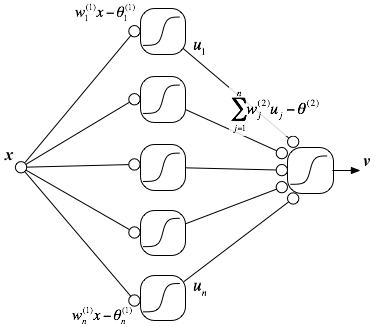
まず、入力$x$に重みを掛つつシフトした値を、$f$で変換する。 この変換を何通りも考えることにすると、$i$番目の変換の結果は $$ u_i = f\left(w^{(1)}_i x - \theta^{(1)}_i \right) $$ と表現できる。ここで、上付き添字の$(1)$は（微分ではなく）「１段目の変換」を表すために付けた。 また、「1段目の変換ユニット」は$n$個用意するとしよう。

次に、$u_i$の組に対して、同じような操作を行う。すなわち、 $$ v = f\left( \sum_{j=1}^n w^{(2)}_j u_j - \theta^{(2)} \right) $$ ここで、上付き添字の$(2)$は「2段目の変換」を表す。 入力$x$が2段階の処理を経て「統合」され、出力$v$が得られる、という流れを図で表現したのが以下である：

上記は、中間層付きのフィードフォワード型のニューラルネットワークと呼ばれている。 そして、このモデルに登場するパラメータ$ \{w^{(1)}_i\}, \{ \theta^{(1)}_i\}, \{ w^{(2)}_i\}, \theta^{(2)} $ の値をうまく調整することによって $$ v \approx y = g(x) $$ となるようにする方法を考えるのが、ここでの主題である。

教師信号による誤差の最小化

正しい入力と出力の組 $(x^1, y^1), (x^2, y^2), \cdots, (x^k, y^k), \cdots, (x^N, y^N)$ が与えられているような状況を考えよう。 ここで、上付き添字は累乗の意味ではないことに注意。 このとき、$y^k$ は教師信号と呼ばれる。 与えられた入力$x^k$に対して、できるだけ教師信号に近い値を出力することをゴールに設定すると、 ひとつの指標として、自乗誤差の総和 $$ E = \sum_{k=1}^N \left( v^k - y^k \right)^2 $$ を評価関数として、これが最小にになるようにパラメータを決めるというのが、自然な発想である。 つまり、ニューラルネットワークによる関数の近似は、（複雑なモデルの）最小二乗法の一種とみなすことができる。

$E$が最小となるパラメータを直接的に求めるのは難しいため、通常は、逐次的な方法が採られる。 $w^{(1)}_i$等のパラメータを記号 $\xi$ で代表して表すことにしよう。 いちばん最初は $\xi$ に「適当な」（例えばランダムな）値を設定しておいて、 $$ \xi \to \xi - \epsilon \frac{E(\{\xi\})}{\partial \xi} $$ によって更新する操作を反復する。ここで$\epsilon$は十分「小さな」値とする。 すると、パラメータの組は$E$の勾配を下って、$E$が極小となる点までたどり着くことができるはずである。

評価関数の微分は $$ \frac{E(\{\xi\})}{\partial \xi} = \frac{\partial \sum_{k=1}^N \left( v^k - y^k \right)^2}{\partial \xi} = \sum_{k=1}^N \frac{\partial \left(v^k - y^k \right)^2}{\partial \xi} $$ を、以下のように、具体的に計算することによって評価できる。

評価関数の$k$番目の項を、$w^{(2)}_j$と$\theta^{(2)}$でそれぞれ偏微分し、合成関数の微分とチェインルールを適用すると、 $$ \begin{eqnarray} \frac{\partial (v^k - y^k)^2}{\partial w^{(2)}_j} & = & 2 (v^k - y^k) \frac{\partial v^k}{\partial w^{(2)}_j} \\ & = & 2 (v^k - y^k) \, f'\left( \sum_{j=1}^n w^{(2)}_j u^k_j - \theta^{(2)} \right) \,u^k_j \end{eqnarray} $$ および $$ \begin{eqnarray} \frac{\partial (v^k - y^k)^2}{\partial \theta^{(2)}} = - 2 (v^k - y^k) \, f'\left( \sum_{j=1}^n w^{(2)}_j u^k_j - \theta^{(2)} \right) \end{eqnarray} $$ となる。

中間層のパラメータについての微分についても、微分のチェインルールを先まで進めることで、 $$ \begin{eqnarray} \frac{\partial (v^k - y^k)^2}{\partial w^{(1)}_i} & = & 2 (v^k - y^k) \frac{\partial v^k}{\partial w^{(1)}_i} \\ & = & 2 (v^k - y^k) \, f'\left( \sum_{j=1}^n w^{(2)}_j u^k_j - \theta^{(2)} \right) \sum_{j=1}^n w^{(2)}_j \frac{\partial u^k_j}{\partial w^{(1)}_i} \\ & = & 2 (v^k - y^k) \, f'\left( \sum_{j=1}^n w^{(2)}_j u^k_j - \theta^{(2)} \right) w^{(2)}_i f'\left( w^{(1)}_i x - \theta^{(1)}_i \right) x^k \end{eqnarray} $$ および、 $$ \begin{eqnarray} \frac{\partial (v^k - y^k)^2}{\partial \theta^{(1)}_i} = - 2 (v^k - y^k) \, f'\left( \sum_{j=1}^n w^{(2)}_j u^k_j - \theta^{(2)} \right) w^{(2)}_i f'\left( w^{(1)}_i x - \theta^{(1)}_i \right) \end{eqnarray} $$ が得られる。

この式をよく眺めると、出力の誤差 $v^k - y^k$ が、活性化関数の微分$f'(\cdot)$を介しながら、前段方向に「伝達」されるような格好になっていることから、 これを使ってパラメータの調整（学習）を行う手法は誤差逆伝播（バックプロパゲーション）法と呼ばれている。 この調整ルールは、ネットワークの中間層の数が増えても式中に同様の形： 

(出力段の誤差)×(出力段の微分)×(前段への荷重)×(前段の微分)×(前々段への荷重)×(前々段の微分)×(前々々段への荷重)×(前々々段の微分)×・・・・

を含むことになる。掛け算の過程で、微分が0に近い箇所があると全体としての勾配が非常に小さくなり（勾配消失）、逆に、1より大きな値が連続すると勾配が爆発する可能性もあり、 多段の（深い）ニューラルネットの学習の困難さの一因となっていた。 こうした困難を克服するために、ディープニューラルネットワークにおいては、様々な工夫が凝らされている。

関数近似（学習）のシミュレーション

では、上で説明した関数を近似するニューラルネットワークの動作を、コンピュータ上でシミュレーションしてみよう。 以下のPythonコードはKerasと呼ばれる機械学習用フレームワークを使って、入力1、中間層12、出力1素子のネットワークを構成し、 関数 $$ y = (\cos(x) + 1)/2 $$ を学習させる例である（$-\pi \lt x \lt \pi$）。

NumPyの配列x_trainが前節の説明の$\{x^k\}$に、y_trainが$\{y^k\}$に対応しており、自乗誤差を最小化するように学習が進められる。 計算を繰り返しながら（このコードでは100回）、テスト用データ（x_test, y_test）を使って誤差の大きさが評価される。 最後に、学習後のネットワークを使って、x_testに対する予測値（近似値）がプロットされる。

from keras.models import Sequential
from keras.layers import Dense, Activation
from keras import optimizers
import numpy as np
import matplotlib.pyplot as plt

x_train=np.random.uniform(-np.pi,np.pi,1000)
y_train=(np.cos(x_train) + 1)/2

x_test=np.random.uniform(-np.pi,np.pi,100)
y_test=(np.cos(x_test) + 1)/2

model = Sequential()
model.add(Dense(12, input_dim=1, activation='sigmoid', use_bias=True))
model.add(Dense(1, use_bias=True, activation='sigmoid'))

model.compile(loss='mean_squared_error', optimizer='Adam')

model.fit(x_train, y_train, epochs=100, verbose=1, validation_data=(x_test, y_test))

result = model.predict(x_test)

y_predict = result[:,0]

plt.scatter(x_test, y_test)
plt.scatter(x_test, y_predict)
plt.show()

右のコードの動作結果例。オレンジ色が予測（近似）値、ブルーが正確な値。

icon-pc　練習：近似精度の向上

上のコードをのままでは、あまり精度よく関数が近似できているとは言えない。より精度を上げるための工夫を施してみなさい。例えば、

等々。