Pythonプログラミング（決定木）

事象の分割と情報量

ある感染症の患者の年代と回復または死亡の別のデータが与えられたとしよう。 致死率はそれほど高いわけではないが、死者は高齢者 に多い傾向が見られる。 死亡と年齢との間の、情報論的な結びつきの程度を、相互情報量を使って測ってみよう。

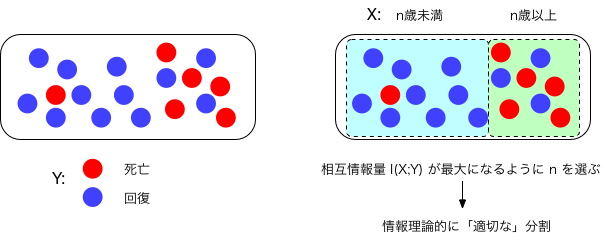
例えば、患者の年代を$X$（例えば「60歳未満」と「60歳以上」）、死亡したかどうかを$Y$（「死亡」と「回復」）としたとき、 相互情報量は $$ I(X;Y) = \sum_x \sum_y p(x,y) \log_2 \left( \frac{p(x,y)}{p(x) p(y)} \right) $$ で与えられる。 ここで、$x$は「60歳未満」と「60歳以上」、$y$は「死亡」と「回復」について、それぞれ和を取るものとする。 もし、$X$と$Y$が独立であれば、相互情報量は0を、そうでなければ正値をとる。

ここで、$X$の定義を「$n$歳未満」と「$n$歳以上」という風に一般化した上で、 $n$の値を変えながら相互情報量 $I(X(n);Y)$ の違いを調べたとしよう。 そして、ある$n=n^*$のところで相互情報量が最大になったとすると、 「死亡」か「回復」かについての情報との関係性が最大となるような データの分割方法（「$n^*$歳未満」と「$n^*$歳以上」）が得られたことになる。

相互情報量と情報の利得

相互情報量は、情報エントロピー $H(X), H(Y)$、条件付きエントロピー$H(X|Y), H(Y|X)$、そして結合エントロピー$H(X,Y)$と $$ \begin{eqnarray} I(X;Y) & = & H(X) - H(X|Y) \\ & = & H(Y) - H(Y|X) \\ & = & H(X) + H(Y) - H(X,Y) \end{eqnarray} $$ の関係がある。 ここで、これらの量を具体的な計算手順は $$ \begin{eqnarray} H(X) & = & - \sum_x p(x) \log_2 p(x) \\ H(Y) & = & - \sum_y p(y) \log_2 p(y) \\ H(X,Y) & = & - \sum_x \sum_y p(x,y) \log_2 p(x,y) \\ \end{eqnarray} $$ および $$ \begin{eqnarray} H(X|Y) = - \sum_y p(y) \sum_x p(x|y) \log_2 p(x|y) = - \sum_x \sum_y p(x,y) \log_2 p(x|y) \\ H(Y|X) = - \sum_x p(x) \sum_y p(y|x) \log_2 p(y|x) = - \sum_x \sum_y p(x,y) \log_2 p(y|x) \\ \end{eqnarray} $$ である。

ここで、$H(Y) - H(Y|X)$ の意味するところは、$Y$についての平均情報量と、$X$を知った上での$Y$についての情報量$H(Y|X)$の差、 すなわち、$X$についての知ることによって、どれだけの情報利得（ゲイン）が得られたか、と解釈できる。 このとき、$X$と$Y$の役割は対称なので、同じことを$H(X)- H(X|Y)$と表現することもできるというわけである。

また、エントロピーは必ず非負となるから、$Y$を与えた際に、情報ゲインを最大化するような$X$を見出すことは、 条件付きエントロピー $H(Y|X)$ を最小化することに他ならない。

COVID-19の患者データの分析

SIGNATEのウェブサイトに掲載されているCOVID-19の患者データを元に、 経過が明らかな約8400件について、 患者の年代（年齢が$0,10,20,\cdots,80$歳代以上)、性別（0:女性,1:男性）、経過（0:回復,1:死亡）をCSVにまとめたファイルを こちらに用意した。

これを読み込んで、$X$として「$n$歳代未満」と「$n$歳代以上」、$Y$として死亡の有無を採用し、 10きざみで$n$を変えながら相互情報量$I(X;Y)$を求めるコードの例を以下に示した。

# coding: utf-8

import pandas as pd
import numpy as np
import math

data = pd.read_csv('covid-19-age-sex-death.csv')

age = data['年代'].tolist()
sex = data['性別'].tolist() # 0:femail 1:male
death = data['死亡'].tolist() # 0:recovered 1:dead

for threshold in range(20,100,10):
    px = np.zeros((2,))
    py = np.zeros((2,))
    pxy = np.zeros((2,2))
    n = len(age)
    for i in range(n):
        a = age[i]
        s = sex[i]
        d = death[i]

        py[d] = py[d] + 1

        if a < threshold:
            px[0] = px[0] + 1
            pxy[0,d] = pxy[0,d] + 1
        else:
            px[1] = px[1] + 1
            pxy[1,d] = pxy[1,d] + 1

    px = px/n
    py = py/n
    pxy = pxy/n

    hx=0
    for x in range(2):
        if px[x]>0:
            hx = hx - px[x] * math.log2(px[x]) 

    hy=0
    for y in range(2):
        if py[y]>0:
            hy = hy - py[y] * math.log2(py[y]) 

    hxy=0
    for x in range(2):
        for y in range(2):
            if pxy[x,y]>0:
                hxy = hxy - pxy[x,y] * math.log2(pxy[x,y]) 

    IXY = hx + hy - hxy
    print('threshold age: {0}  IXY= {1:.4f} [bit]'.format(threshold,IXY))

このコードを実行すると

threshold age: 20  IXY= 0.0006 [bit]
threshold age: 30  IXY= 0.0042 [bit]
threshold age: 40  IXY= 0.0071 [bit]
threshold age: 50  IXY= 0.0108 [bit]
threshold age: 60  IXY= 0.0170 [bit]
threshold age: 70  IXY= 0.0191 [bit]
threshold age: 80  IXY= 0.0128 [bit]
threshold age: 90  IXY= 0.0024 [bit]

が得られるので、情報量ゲインが最も大きいのは $n=70$ であることが分かる。 すなわち、新型コロナに罹患して死亡する可能性の高い群は、70歳代以上とそれ未満に分けられる。 ただし、高齢者の致死率は相対的に大きいとはいえ、数%程度であるため、情報量のゲインはそれほど大きくは無い。

　練習：性別での情報ゲイン

上記のコードで用いたデータ（covid-19-age-sex-death.csv）は、患者毎の年代、性別、死亡の有無の情報が含まれている。 コードを元に、年代（$n$歳未満、以上）ではなく、 男女の別を$X$と置いた場合の情報ゲインを計算してみなさい。

分割の別の指標

相互情報量を用いた分割の意味は理解しやすいが、計算を行う手間が煩雑となってしまう。 それに代わる指標として、ジニ指標（Gini index, またはジニ不純度(Gini impurity measure)）がよく用いられる。 $M$個のカテゴリーに分けられた対象の中で、$k$番目のカテゴリーに属するものの割合（確率）を $p_k$ とすると、 ジニ指標は $$ G = 1 - \sum_k^M {p_k}^2 $$ で定義される。

例えば、あるグループの中の「死亡」の患者の率が$p$、「回復」が$1-p$とすれば $$ G = 2 \, p \, (1-p) $$ となる。 これは、$p=0$と$p=1$で最小(0）で、$p=1/2$で最大となる放物線である。

ここで、条件$x$（例えば「$n$歳未満」と「$n$歳以上」）のもとで、$y$が見いだされる確率から、 「条件付き」のジニ指標 $G(y|x)$ を求め、それを条件付きエントロピー $H(Y|X)$ に類する量と考えると、 平均的なジニ指標 $$ \sum_x p(x) G(y|x) $$ を最小にすることで、情報ゲインを大きくできると期待される。

このジニ指標を使って、前節と同じデータについて、ゲインを計算するコードの例を以下に示した：

# coding: utf-8

import pandas as pd
import numpy as np
import math

data = pd.read_csv('covid-19-age-sex-death.csv')

age = data['年代'].tolist()
sex = data['性別'].tolist() # 0:femail 1:male
death = data['死亡'].tolist() # 0:recovered 1:dead

for threshold in range(20,100,10):
    px = np.zeros((2,))
    pyx = np.zeros((2,2))
    n = len(age)
    for i in range(n):
        a = age[i]
        s = sex[i]
        d = death[i]

        if a < threshold:
            px[0] = px[0] + 1
            pyx[d,0] = pyx[d,0] + 1
        else:
            px[1] = px[1] + 1
            pyx[d,1] = pyx[d,1] + 1

    pyx[:,0] = pyx[:,0] / px[0]
    pyx[:,1] = pyx[:,1] / px[1]
    px = px/n

    G=0
    for x in range(2):
        g = 1
        for y in range(2):
            g = g - pyx[y,x]**2
        G = G + px[x] * g

    print('threshold age: {0}  G= {1:.4f}'.format(threshold,G))

実行してみると、相互情報量を用いた場合の計算と同じ年齢で、ジニ指標が最小になっていることが確認できる。

threshold age: 20  G= 0.0284
threshold age: 30  G= 0.0283
threshold age: 40  G= 0.0282
threshold age: 50  G= 0.0281
threshold age: 60  G= 0.0277
threshold age: 70  G= 0.0274
threshold age: 80  G= 0.0275
threshold age: 90  G= 0.0282

決定木の作成

以上のように、年齢や性別などの属性情報に基づき、相互情報量の最大化（またはジニ指標の最小化）を指標として、データをサブグループに分けることができる。 ここでは簡単のため、２つにグループ分けする場合のみを考えるが、それ以上に分けることも可能である。

こうして得られたサブグループに対しても、同様の手続きを再帰的に行うことで、結果（「死亡」か「回復」かなど）に対する寄与の大きな因子を、 ツリー状に表現することができ、決定木（decision tree)と呼ばれている。

複数の因子を持つ大きなデータに対して決定木を構成するのは、計算量を抑えるためのアルゴリズムの工夫が必要でコーディングも複雑になるため、ライブラリとして提供されている。 ここでは、scikit-learnライブラリに実装されている分類器を用いて、前節で用いたCOVID-19の患者データを処理するコードの例を示す。

# coding: utf-8

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from graphviz import Source

data = pd.read_csv('covid-19-age-sex-death.csv')

age = data['年代'].tolist()
sex = data['性別'].tolist() # 0:femail 1:male
death = data['死亡'].tolist() # 0:recovered 1:dead

n = len(death)

train_data = np.empty((n,2))
for i in range(n):
    train_data[i,0] = age[i]
    train_data[i,1] = sex[i]

target_data = np.array(death)

cls = DecisionTreeClassifier(max_depth = 2,criterion="entropy")
cls.fit(train_data, target_data)

src = Source(export_graphviz(cls))
src.render('covid-19-dtree', view=True, format='pdf')

　練習：旅行の口コミ情報の分析

情報基礎A/Bの演習用に、旅行サイトが収集した宿泊施設の評価に関するアンケートデータが提供されている。 データは、宿泊施設の「立地」, 「部屋」, 「食事」, 「風呂」, 「サービス」, 「設備」, そして「総合」について、 1から5までの5段階で客ごとに尋ねた結果をCSVファイル(travel_data.csv)にまとめたもので、 「情報とデータの基礎」教材(東北大学内限定)からダウンロードできる。

上記のコード例を参考に、 総合評価が5（最高評価）を1、それ未満を0、とし、「立地」から「設備」までの6つの属性情報によって、決定木を構成するコードを作成し、 その出力結果を解釈してみなさい。

　解説:「不平等」の指標

$N$人の集団（例えば国民）の所得の分布について考えてみる。 一般に、金持ちは比較的少数で、低所得者が相対的に多い傾向が見られるが、それが行き過ぎると「格差」が問題となる。 そこで、どの程度、所得が平等に（あるいは不平等に）分配されているかの定量的な指標としてよく議論されるのがジニ係数である。

集団を所得の昇順に並べ替え、（低いほうから）$i$番目の人の所得を $q_i$ と書くことにしよう。すると、$n$番目の人までの所得の合計は $$ Q_n = \sum_{i=1}^n q_i $$ であり、集団全体の総所得は $Q_N$ である。 そこで、 $$ P_n = Q_n / Q_N $$ を定義すれば、これは$n$に応じて最大1までの値を取る。

一方で、$n$番目の所得の人の相対的なランキングは $$ R_n = n / N $$ であり、こちらも$1/N$から1までの値を取る。1が最も高所得の人に対応する。

所得が完全に平等に分配されるときは、個人の所得は総所得の$1/N$倍になるので、 $$ Q_n = \sum_{1=1}^n \frac{Q_N}{N} = \frac{n Q_N}{N} $$ で、$P_n = n / N$、すなわち $$ P_n = R_n $$ であり、２つの量は勾配１で比例する。

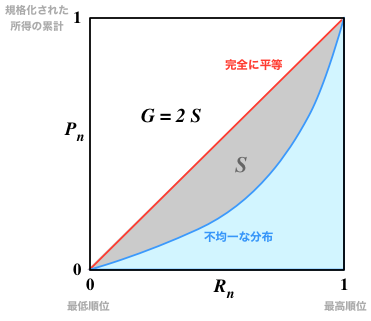
所得に格差が生じている場合は、高所得者側に全体の所得が多く分配されるので、図のように、$R_n$と$P_n$は、下に凸の形状に変わる。 実際に計算すると、その面積の比率は$N$が十分大きければ（台形近似で） $$ G = 1 - \frac{2}{N} \left[ \sum_{n=1}^{N-1} P_n + \frac{1}{2} \right] $$ となり、これはジニ係数(Gini coefficient)と呼ばれている。0が完全に平等な場合、1が少数（一人）に所得が集中している場合に相当する。

このジニ係数、そして決定木の生成過程の分類に用いたジニ指標のいずれも、 イタリアの統計学者Corrado Giniによって考案された。 名称が紛らわしいが、これらは別物である。