Pythonプログラミング(K近傍法によるクラス分類)
このページは、データ点を分類する基本的なアルゴリズムのひとつであるk近傍法について紹介する。
「基準」が示されている場合のデータの分類:k近傍法
あなたはカーナビを設計しているとしよう。 その内部には、データとして、いくつかのランドマーク(例えば市役所や役場)の座標が、それらが属する行政区と共に登録されていると仮定しよう。 実際にGPSから得られる現在地の座標情報から、現在、どの市町村にいるのかを表示するようにプログラムしたいとすると、 登録済みの情報(ランドマークの座標)からどのように行政区を割り出せばよいだろうか。
すぐに思いつくのは、『現在位置から最も近いランドマークを探し、そのランドマークが属する行政区を現在位置の行政区とみなす』 やり方であろう。
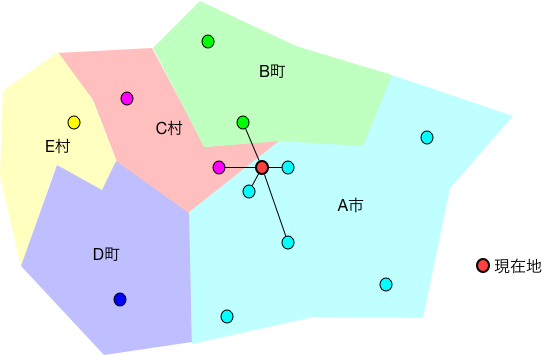
ところが、行政区の境界が入り組んでいるような場合は、これでは判断を誤る可能性も出てくる。 そこで、『現在位置から近い順に$k$番目までのランドマークを探し、そのランドマークが属する行政区を「多数決」して得られたものを、現在位置の行政区とみなす』 というふうに、判定基準を修正する。 例えば、$k=5$の場合、ランドマークが A市、B町、A市、A市、C村、であったら、現在位置はA市内とみなす(下図)。
ある点から一番近い点を第1近傍、2番目に近い点を第2近傍、等と呼ぶことから、この方法は k近傍法(k-nearest neighbor algorithm)と命名されている。 上記の例は2次元座標を想定していたが、任意の次元のデータでもアルゴリズムは全く同様である。
雪のかたち
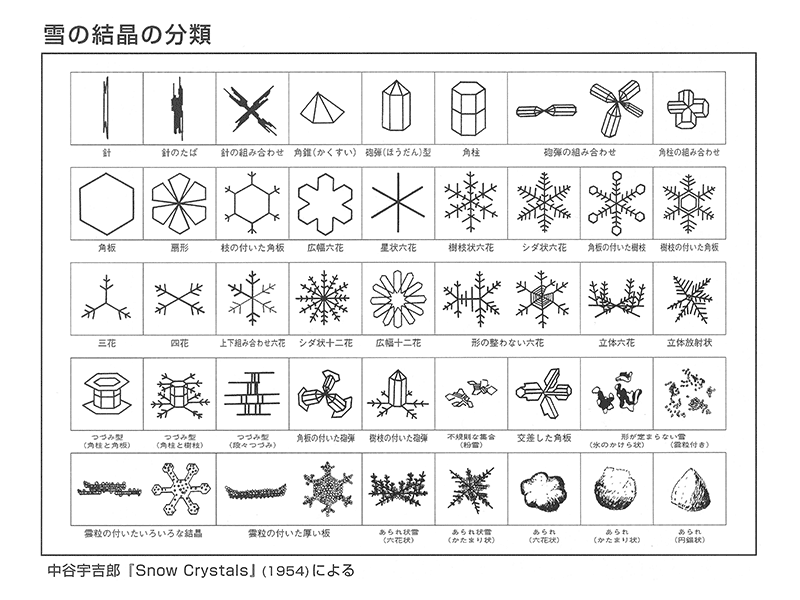
雪国で生活したことのある方ならば、雪の結晶の形は、気象条件によって様々に変化することを経験的に知っているだろう。 こうした雪の結晶形の研究で世界的に知られているのが中谷宇吉郎である。 以下は中谷が観察し分類した雪の結晶形である。この中で、我々がすぐに想像する6角形の枝分かれした雪華のイメージに対応するのが「樹枝状」である。
図はhttps://yukinokagakukan.kagashi-ss.com/からのリンク
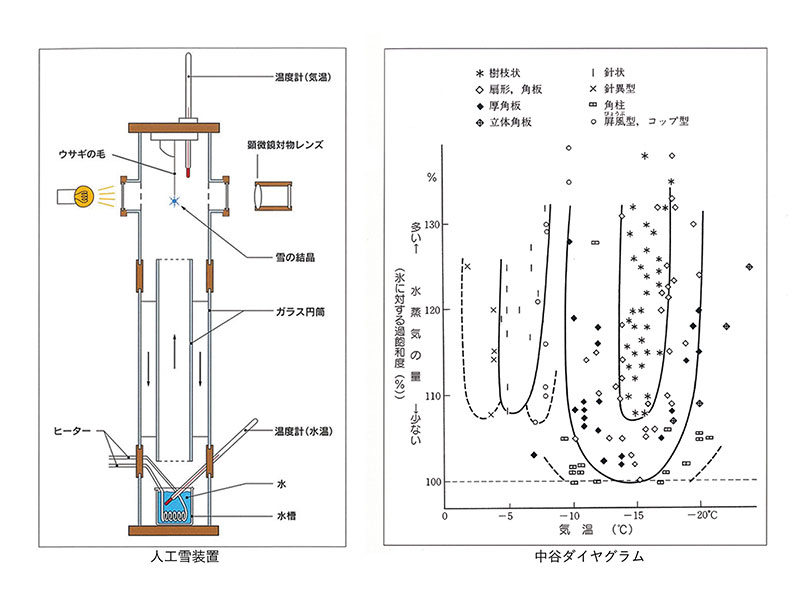
中谷は人工的に雪を作る装置を考案し、さまざまに条件を変えながら実験することで、雪の結晶の形を決める主な要因は、空気中の水蒸気量(過飽和度)と気温であることをつきとめた。 それを図で表したのが中谷ダイアグラム(The Nakaya snow crystal morphology diagram)である。
図はhttps://yukinokagakukan.kagashi-ss.com/からのリンク
ここでは、上図(右)の中谷ダイアグラムのデータ点を元に、形態を数値(分類番号)として
樹枝状 0 針状 1 扇型、角板 2 針異型 3 厚角板 4 角柱 5 立体角板 6 屏風型、コップ型 7
と置き直した上で、
気温(C) 過飽和度(%) 形態を表す分類番号
の形に整理したデータファイル:nakaya-data.txt を用意した。
以下では、中谷ダイアグラムを「地図」、データ点を「ランドマーク」、雪の結晶の形態を「行政区」に対応づけ、気温と過飽和度を入力すると、k近傍法をつかってその条件下で予想される雪の形態を出力するコードを作成してみよう。
k近傍法の実装
中谷ダイアグラムのデータを読み込んで、温度(摂氏)と過飽和度(%) の入力を求め、k近傍のクラスを出力するPythonコードの例を以下に示す。
かなり非効率ではあるが、処理の流れは以下のとおり:
- データファイルnakaya-data.txtを読み込み、リスト
linesに各行を格納 - NumPyの二次元配列
xに [温度,過飽和度,分類番号] に格納 - 温度と過飽和度を入力(
temp, ssat - 入力値からの距離と分類番号を、NumPyの配列
yに格納 yを距離をキーにして並べ替え- NumPyの配列
catsを0にセットして - 距離が$k$番目までの分類番号ごとにカウント
np.argmax()関数で最もカウント数の大きな分類番号を得て、出力
# coding: utf-8
import numpy as np
# データファイルの読み込み
with open('nakaya-data.txt') as file:
lines = file.readlines()
x = np.empty((0,3))
for line in lines:
d = line.split()
t = float(d[0])
s = float(d[1])
c = int(d[2])
x = np.append(x, np.array([[t,s,c]]), axis=0)
# 温度の過飽和度の入力
temp = float(input('temperature[C]:'))
ssat = float(input('supersaturation[%]:'))
# 入力値からの距離が近い順に並べ替え
dtype2=[('dist', float) , ('cat', int)]
y = np.empty((x.shape[0],), dtype=dtype2)
for i,[t,s,c] in enumerate(x):
dist = np.sqrt( (t-temp)**2 + (s-ssat)**2 )
y[i] = (dist,c)
y = np.sort(y,order="dist")
# k(以下では3)近傍内のデータ点を確認
k = 3
cats = np.zeros((10,))
for cnt,item in enumerate(y):
if cnt>=k:
break
i = item['cat']
cats[i] = cats[i]+1
# 出現回数の多いデータのカテゴリを出力
cat = np.argmax(cats)
print('カテゴリー番号:',cat)
コード中に用いているNumPy等の機能について補足する:
x = np.empty((0,3))- 0行3列の空の配列を生成
x = np.append(x, np.array([[t,s,c]]), axis=0)- 配列に、
[t,s,c]という行を追加 y = np.empty((x.shape[0],), dtype=[('dist', float) , ('cat', int)])- 配列
xの行数分のサイズの配列を生成。配列の要素は'dist'と'cat'と名付けられた2つのフィールドを持つ。 y = np.sort(y,order="dist")- 配列
yを'dist'フィールドをキーにして整列する。 cat = np.argmax(cats)- 配列
catsの中で、内容が最大値である要素の添字を得る。
上記を元に、カテゴリー番号0(樹枝状結晶)の領域を描画するように修正したコードと出力結果の例を示す:
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
with open('nakaya-data.txt') as file:
lines = file.readlines()
x = np.empty((0,3))
for line in lines:
d = line.split()
t = float(d[0])
s = float(d[1])
c = int(d[2])
x = np.append(x, np.array([[t,s,c]]), axis=0)
T = np.arange(-30,0,1)
S = np.arange(100,135,2)
Z = np.zeros((T.shape[0],S.shape[0]))
k = 3
for i_t,temp in enumerate(T):
for i_s,ssat in enumerate(S):
dtype2=[('dist', float) , ('cat', int)]
y = np.empty((x.shape[0],), dtype=dtype2)
for i,[t,s,c] in enumerate(x):
dist = np.sqrt( (t-temp)**2 + (s-ssat)**2 )
y[i] = (dist,c)
y = np.sort(y,order="dist")
cats = np.zeros((10,))
for cnt,item in enumerate(y):
if cnt>=k:
break
i = item['cat']
cats[i] = cats[i]+1
cat = np.argmax(cats)
if cat==0:
Z[i_t,i_s]=1
else:
Z[i_t,i_s]=0
plt.title("Nakaya diagram")
plt.contourf(T, S, Z.T)
plt.colorbar(orientation="vertical")
plt.xlabel('TEMPERATURE[C]')
plt.ylabel('SUPERSATURATION[%]')
plt.show()
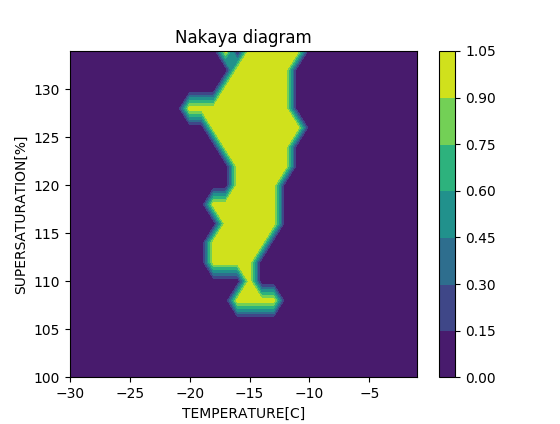
黄色い箇所が $k=3$ の場合に 、樹枝状結晶に分類される領域。 論文の中谷ダイアグラムとは横軸の向きが反転していることに注意。
このプロットから、樹枝状の雪が降るのは、気温が-15度程度、水蒸気量が110%以上の条件下であることが見て取れる。
 練習:k近傍法の動作確認
練習:k近傍法の動作確認
上記のコードを動かして、分類がうまくいくかどうか、動作を確認してみなさい。 また、「樹枝状」の代わりに、他の結晶形の領域を表示するよう、上記のコードを変更してみなさい。
さらに、k近傍法で誤った分類結果となるとしたら、それはどのような場合が想定されるか、考えなさい。