Pythonプログラミング(階層的なクラスタリング)
このページは、階層的なクラスタリングの考え方と例を紹介する。
データ点の類似度
データ点 $x$ と、データ点 $y$ の間の距離を $$ d(x,y) $$ で表すことにしよう。 ここで、 $d(x,y) \ge 0$で、$d(x,y)=0$のときに$x=y$(データは同一)となるように距離を定義する。 そして、距離が小さいほど、2つのデータは近い(類似性が高い)と解釈する。
距離の定義の仕方としては、ベクトル間のユークリッド距離 $$ d(\boldsymbol{x},\boldsymbol{y}) = \sqrt{ \sum_i^d (x_i - y_i)^2 } $$ に限らず、データの種類や目的に応じて任意に選択できる。 さらに、発想を拡張して、データ点のグループ同士の距離を考えることもできる。
クラスター間の距離
次に、データ点の集まりをひとつのグループ(クラスター)とみなし、複数のそうしたクラスターが存在するような状況を考えてみよう。 例えば、データ点を町の住宅の位置、クラスターを町と考えれば、A, B, C...、という複数の町が存在するようなイメージである。 そのとき、クラスター間の距離をどのように決めればよいだろうか。 定義のやり方は何通りも提案されているが、ここでは、3つの代表的な方法を紹介する。
最短距離法
クラスターA と クラスターBに属するデータ点を、それぞれ $\boldsymbol{x}_A$, $\boldsymbol{x}_B$ と表記することにする。 そしてそれぞれのクラスターからデータ点をひとずつ選んで(Aからは$i$番目の点 $\boldsymbol{x}^i_A$, Bからは$j$番目の点$\boldsymbol{x}^j_B$)、それらの距離 $$ d(\boldsymbol{x}^i_A, \boldsymbol{x}^j_B) $$ を求めれば、クラスター間の距離の目安になるはずである。 A町の$i$さん宅と、B町の$j$さん宅の距離を測れば、それが町の距離の目安になるのと同様である。
中でも、$i$と$j$の距離の最小値 $$ d(A,B) = \min_{i \in A, j \in B} d(\boldsymbol{x}^i_A, \boldsymbol{x}^j_B) $$ は、ふたつのクラスターがどの程度隣接しているかの目安と解釈でき、クラスター間の距離の指標として使われる。
群平均法
クラスターの代表的な2点($i \in A$と$j \in B$)間の距離を取っただけでは、$i$と$j$の選び方で結果が大きく変動してしまう。 そこで、クラスターの平均的な隔たりの指標として、全てのペアについて等しい重みで取った平均 $$ d(A, B) = \frac{1}{N_A N_B} \sum_{i \in A} \sum_{j \in B} d(\boldsymbol{x}^i_A, \boldsymbol{x}^j_B) $$ もよく用いられる。ここで、$N_A$はクラスターAの、$N_B$はBのデータ点の数である。
Ward法
クラスターの「大きさ」、あるいは「広がり具合」の指標を考えてみる。 $\boldsymbol{x}^i$があるクラスターに属するデータ点、 それらの重心を $$ \bar{\boldsymbol{x}} = \frac{1}{N} \sum_i \boldsymbol{x}^i $$ とすると、各点の代表点(重心)からの二乗和 $$ \sum_{i} \| \boldsymbol{x}^i - \bar{\boldsymbol{x}} \|^2 $$ がそのよい目安になっているであろうと直感できる。
ここで、2つのクラスターA, Bが与えられたとき、それらをひとつのクラスターにまとめた際に、上記の指標がどの程度変化(増加)するかを評価してみる。 $$ \Delta_{A,B} = \sum_{i \in A,B} \| \boldsymbol{x}^i - \bar{\boldsymbol{x}_{A,B}} \|^2 - \sum_{i \in A} \| \boldsymbol{x}^i - \bar{\boldsymbol{x}_{A}} \|^2 - \sum_{i \in B} \| \boldsymbol{x}^i - \bar{\boldsymbol{x}_{B}} \|^2 $$ この増加分が小さいほど、2つのクラスターは「近い」と言えるだろう。 そして、これを、2つのクラスター間の距離と見なす: $$ d(A,B) = \Delta_{A,B} $$
右の関係を漸化式として整理したものはLance-Williamsの更新式と呼ばれている。
上のようにデータ点の隔たりをユークリッド距離で定義する場合は、増分を求める際に併合したクラスターについて改めて二乗和の計算する必要はなく、 重心とデータ点の数から $$ \Delta_{A,B} = \frac{N_A N_B}{N_A + N_B} \| \bar{\boldsymbol{x}}_{A} - \bar{\boldsymbol{x}}_{B} \|^2 $$ となる。
 練習: 確認計算
練習: 確認計算
上記の$\Delta_{A,B}$の式が成り立つことを確認してみなさい。
クラスタリング
k-means法によるクラスタリングでは、クラスターの個数をあらかじめ決めておかねばならないため、分析に先立ってデータの特徴をある程度把握しておかねばならないところに難がある。 一方、以下のボトムアップな手順に従って、段階的により大きなクラスターにまとめる方法を採ることで、先験的な知識や前提無しに、クラスターを自動的に生成することができる:
- 初期状態として、データ点はそれぞれデータ数1のクラスターと考える。
- クラスターのペアを調べ、距離が最小のペアを併合して一つのクラスターにまとめる。
- 2を、全体がひとつのクラスターになるまで繰り返す。
クラスタリングのコードを書くのはいささか骨が折れるので、 以下ではSciPyの階層クラスタリング用ライブラリを用いて、サンプルデータのクラスタリングを行い、 結果をデンドログラム(dendrogram)と呼ばれる形式で出力するコード例を示した。
linkage関数はベクトルデータを指定された方法(この例ではward法)でクラスタリングし、その結果を行列形式(linkage matrix)として返す。
dendrogram関数は、その情報からデンドログラムをプロットする。
# coding: utf-8
import sys
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage,dendrogram
# 生成するグループの数
k = 4
# グループ毎の分散
sigma = [[20, 0], [0, 20]]
# データ点の生成
x = np.empty((0,2))
for ell in range(k):
pc = np.random.uniform(low=-20, high=20, size=(2,)) # グループ毎の代表点
xs = np.random.multivariate_normal(pc,sigma,30)
x = np.concatenate([x,xs])
# クラスタリング
link = linkage(x,'ward')
labels = range(0, k*30)
# 結果のプロット
dendrogram(link,
orientation='top',
labels=labels,
distance_sort='descending',
color_threshold=40.0,
show_leaf_counts=True)
plt.show()
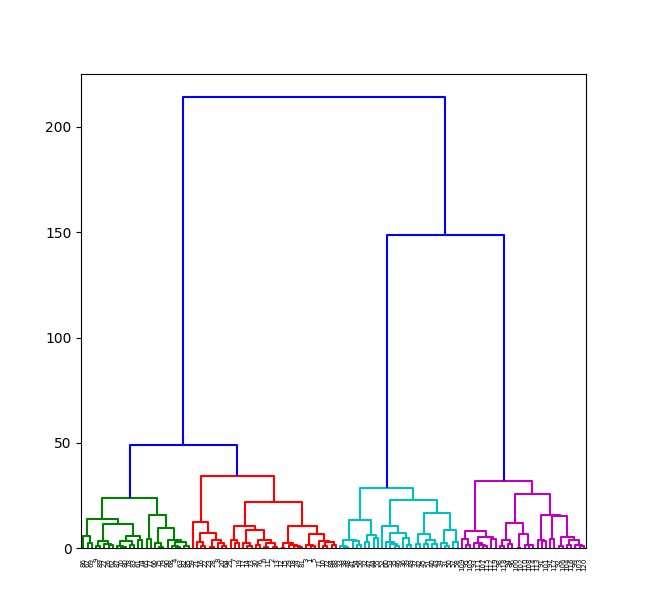
右のコードから出力されたデンドログラムの例
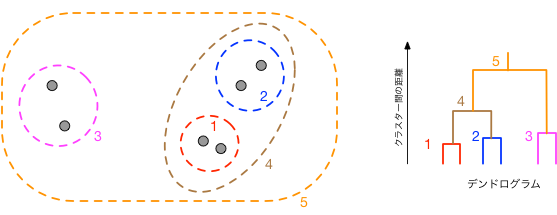
横軸が各データ点に、縦軸がクラスター間の距離を表す。 この図の場合、互いの距離がおよそ50程度以上の範囲でデータ点まとめると、データ点は3つのクラスターに分かれることがわかる。 ツリーをたどることで、どのデータ点がどのクラスターに属しているのかが判る。
同じく、SciPyのlinkage関数を使って、クラスター毎にデータ点を色分けしてプロットする例を示す。
クラスタリングに伴う距離の変化が、コード中程で設定されている変数thresholdの値を超えたら、
そこでクラスターの併合を打ち切り、結果をプロットするようになっている。
linkage関数は、クラスタリングのステップ毎に
[クラスター番号1, クラスター番号2, クラスタリングに伴う距離の変化, 新しいクラスターに属するデータ数]
の配列を出力する。データ総数を$n$とすると、(0番目から始めて)$i$ステップ目のクラスタリングによって、 クラスター番号 $n+i$ のクラスターが生成される。
下記のコードでは、$i$番目のデータ点の属するクラスター番号を、配列 group[i] に記憶し、
冒頭のrewrite_id関数によって、併合後のクラスターに属するデータ点に、
新しいクラスター番号を振り直すように設計している。
階層的クラスタリングの結果を、データ点の色によって出力するコードの例。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage
def rewrite_id(id, link, group, step, n):
i = int(link[step,0])
j = int(link[step,1])
if i<n:
group[i] = id
else:
rewrite_id(id, link, group, i-n, n)
if j<n:
group[j] = id
else:
rewrite_id(id, link, group, j-n, n)
# 生成するグループの数
k = 4
# グループ毎の分散
sigma = [[20, 0], [0, 20]]
# データ点の生成
x = np.empty((0,2))
for ell in range(k):
pc = np.random.uniform(low=-20, high=20, size=(2,)) # グループ毎の代表点
xs = np.random.multivariate_normal(pc,sigma,30)
x = np.concatenate([x,xs])
# クラスタリング
linked = linkage(x,'ward')
n = x.shape[0]
threshold=40
group=np.empty(n,dtype='int32')
step=0
while True:
if step>= n-2:
break
dist = linked[step,2]
if dist>threshold:
break
rewrite_id(step+n, linked, group, step, n)
step=step+1
# 結果のプロット
cmap = plt.get_cmap("tab10")
cids = list(set(group))
print('cluster ids:',cids)
for i in range(x.shape[0]):
ell = cids.index(group[i]) % 10
plt.scatter(x[i,0], x[i,1], color=cmap(ell))
plt.grid(True)
plt.show()
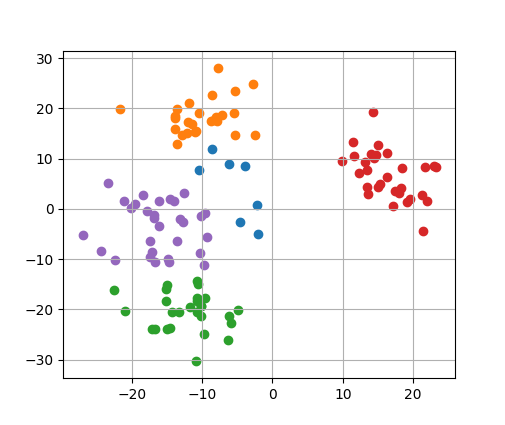
右のコードの実行例。
この例ではデータ点が5つのクラスターに分類されている。
変数thresholdの値を大きくすると、より少数のクラスターに併合される。
 練習:アルゴリズムによる違い
練習:アルゴリズムによる違い
SciPyのlinkage関数のマニュアルを参照し、 Ward法以外に選択可能なクラスター間の距離の定義を調べ、上記のサンプルコードを変更し、動作や違いを確認してみなさい。
 ヒント: 乱数の初期値の設定
ヒント: 乱数の初期値の設定
NumPyの乱数は生成する都度、異なった結果を返すため、アルゴリズムによる結果の差異を比較しにくい。そこで、コードの先頭付近(乱数生成を行う前段)に
np.random.seed(123)
のように、乱数の初期値(タネ)を設定しておくと良い。引数(この例では123)に応じて、決まった系列の乱数が生成される。
 練習:動物の群れの同定
練習:動物の群れの同定
以下の写真は編隊飛行を行うことでよく知られるマガンの群れの例である:
データファイル:geese-skein-20191207.dat
ステレオ画像による解析によって各個体の座標を推定したデータを用意した。 ファイルの各行は、カメラを原点として、個体ごとの 横、奥行き、高さ方向の三次元座標をメートル単位で表している。 写真の群れは、カメラから相対的におよそ45m上空を飛行している。
このデータをクラスタリングすることによって、どの個体がどの群れに属しているかを検出する方法を考察し、検証してみなさい。
 ヒント
ヒント
群れの形が「紐状」であることに着目して、クラスタリングのアルゴリズムを選択すると良い。
ファイルからデータをNumPyの配列に読み込むには、以下のようにすれば良い:
import numpy as np
...
x = np.loadtxt('geese-skein-20191207.dat')
...
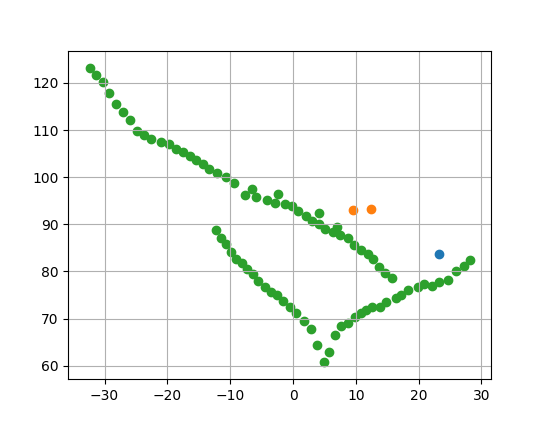
クラスタリングした結果の例を以下に示す。個体の座標を水平面に投影し、クラスター毎に色分けした。