情報基礎A 「Cプログラミング」（ステップ８・パート１）

このステップの目標

• 引数の受け渡し、戻り値の処理、関数の中の変数のスコープを意識し、関数の定義と呼び出しの作法のパターンに従って、プログラムを記述できる
• 複雑な処理を、関数を使って複数の要素に分解・構成できる

１．Cの関数

これまでに登場した色々なＣプログラムの基本骨格は、いつも、

#include <何々>

main() {

    何々;

}

というかたちをしていた。この「意味」について、改めて考えてみたい。

Cプログラムの基本的なルールとして、「括弧 { }で挟まれた箇所は、それ 全体で、一つのまとまりとして解釈される」ことを思い出そう。 正確な例えではないが、文章で言えば、章や段落のようなものだ。

章や節に表題があるように、Cプログラムにも、処理の大きなひとくくりに名前を付けて、 ひとつの処理のまとまりとして「使い回す」ための機構が備わっている。 例えば、main(){何々;} は {何々;}という処理全体に、mainという名前を付けたことになる。 このことを、Cプログラマーは、「mainという名前の関数を定義した」と表現する。

関数というと、sineやcosineなどの数学関数を直ちに連想するだろうが、Cの関数は、 それに似ている面と、かなり異なる面の両方を持ち合わせている。 その違いにはついては、このステップが終了するまでに、明らかになるだろう。

関数の名前は、変数名と区別するために、必ず括弧( )とペアになって登場する。例えばmain()のように。 C言語において、このmain()は特別な関数で、Cプログラムのどこかに必ず定義されていなければならない。 つまり、どんなに単純なプログラムであっても、main(){何々;} という「フレーズ」は、必ず存在する。

これまではmain()という関数が１つだけしか登場しないプログラムばかり扱ってきたが、長い小説には沢山の章があるように、 Cのプログラムでもmain以外の関数を使うことができる。 というより、Cのプログラムは（沢山の）関数の集まりと言ってよい。 そして、複数の関数で構成されるプログラムの外見は、以下のようになる：

#include <何々>

int func() ;
void proc() ;

main() {
    何々;
}

int func(){
    何々;
}

void proc(){
    何々;
}

その他の関数定義が続く・・

要するに、他とは重複しない名前を付けながら、関数の定義を（main()と全く同様に）、箇条書きにするだけである。

２．関数の呼び出しとデータの受け渡し

以前、ステップ２で、三角形の三辺の長さから、面積を計算するプログラムを作成した。 それをベースに、面積を計算する箇所を、Cの関数にまとめたプログラムの例を以下に示した。 ここで新たに定義しているのはarea3という名前の関数である。

#include <stdio.h>
#include <math.h>

void area3(float, float, float) ;

main()
{
  float x,y,z ;
  printf("三角形の三辺の長さ:") ;
  scanf("%f%f%f",&x,&y,&z) ;
  area3(x,y,z) ;
}

void area3(float a, float b, float c)
{
  float s ;
  s = (a+b+c)/2.0 ;
  printf("S= %f\n",sqrt(s*(s-a)*(s-b)*(s-c))) ;
}

関数の呼び出し

a.outでプログラムが実行されると、main( )に書いた処理が順次と実行される。 その途中で、関数名の書かれた箇所にさしかかると、対応する関数の内容が（main()の場合と全く同様に）順に実行される。 関数の処理がひととおり終わると、再びmain()の（その関数を呼び出した箇所の)次から処理が再開される。 この一連の動作を、関数の呼び出し(function call)、と呼ぶ。 この例では、main()関数からarea3()関数を呼び出したが、 どの関数が関数を呼びだしても構わない。 main()関数は、OS（operating system)から呼び出され、その処理が終わると、プログラム全体 が終了する（OSに処理が戻る）ような関数、と考えることができる。

引数（パラメータ）の引渡し

上記の例では、三角形の３つの辺の長さが、関数area3()に受け渡されている様子がすぐに想像できるだろう。

その一連の動作を、整理しておこう。 関数の定義の冒頭のarea3(float a, float b, float c)は、以下のふたつの指示を含意している：

• この関数内でのみ使う変数float a; float b; float c; を宣言する
• これらの変数の初期値は、関数を呼び出す際に、括弧の中の対応する箇所に書いた内容（値）に自動的にセットされる。

この例題の場合、 area3()関数が呼び出されると、呼び出し側のx,y,zの値が、 呼び出される側の変数a,b,cに代入される。 このように、関数に「受け渡される」データを、関数の引数（パラメータ）と呼ぶ。 こうしたデータの受け渡しは、引数のリストの順番にしたがって行われる。 よって、この例では x→a, y→b, z→cという対応関係になる。

こうした一連の動作を以下に図示したので、上の説明と併せて参照すること：

関数のプロトタイプ

この例でちょっと違和感を感じるかもしれないのは、プログラムの冒頭部分の

void area3(float, float, float) ;

の１行だ。これは、関数のプロトタイプ宣言と呼ばれ、コンパイラにarea3()関数の仕様を伝える働きをする。 もしプロトタイプ宣言が無いと、関数main( )の中で、area3( )が呼び出される際に、 Cコンパイラは、どのようにデータの受け渡しを行ったらよいか、知る手立てがない。 このプロトタイプ宣言宣言は「area3( )という関数は、float型の３つの引数を持っており、その処理の終了後、計算結果のデータは 返されない（void:「無し」という意味）」という情報を、コンパイラに告げる役割をしている。

３．戻り値のある関数

上の例題に少しだけ手を加えて、呼び出し側に値を戻す関数を使った例を以下に示す。 この例では、関数area3()で計算した三角形の面積を、呼び出し側で「受け取って」いる。 この動作は、これまでの演習でも使ったsqrt()やsin()等と同様、 「関数」として、自然な動作と言えるかもしれない。

#include <math.h>

float area3(float, float, float) ;

int main()
{
  float x,y,z,s ;
  printf("三角形の三辺の長さ:") ;
  scanf("%f%f%f",&x,&y,&z) ;
  s = area3(x,y,z) ;
  printf("S= %f\n",s) ;
  return 0 ;
}

float area3(float a, float b, float c)
{
  float s ;
  s = (a+b+c)/2.0 ;
  return sqrt(s*(s-a)*(s-b)*(s-c)) ;
}

計算結果を呼び出し側に「戻す」す働きをさせるためには、関数の定義の際に、以下の点に注意が必要である：

• 関数名の前に、その関数が返すデータの型を記述すること。
  例：float area3(float a, float b, float c) ・・・
  目的に応じて、Cの基本データ型int, float, double, charを選択（戻り値が必要無い場合はvoidを指定）。
• 関数内の処理の最後にreturn 式 ;を実行。式の値が呼び出し側に返される（リターンされる）。
  例：return sqrt(s*(s-a)*(s-b)*(s-c)) ;
  return文は、関数のおしまいに限らず、どこに記述してもよい。

これまで、main( )関数の戻り値について注意を払わなかったが、本来、main( )関数は

int main( ) {
    ....
    return 0 ;
}

のように記述すべきである（上の例題ではそのように記述した）。 main()関数の戻り値はプログラムの終了コード(exit code)を表しており、0は「正常な終了」を意味する。 終了コードによって、OSは、そのプログラムがどのような状態で終了したのかを知ることができる。 エラーの発生をOSに伝えたい場合は、0以外の値をreturnすればよい。 ただし、終了コードを気にしなくて良い場合、単にmain() { ... }と書いても構わない。

４．ソフトウェアの部品としての関数

上で述べた例で、関数area3( )が働く様子を、呼び出し側から眺めてみたとすると、（講義担当者の頭の中には）下の様な情景が浮かんでくる。

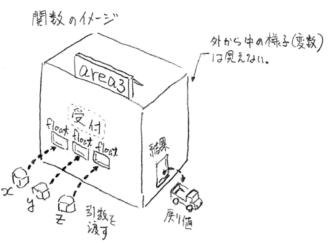
関数の中身はブラックボックスになっていて、中の様子（どんな処理が行われていて、どんな変数が使われているか）はのぞき見ることができない。 ただ、引数に対応する「受付」の窓口があって、そこに、指定されたタイプのデータ（の値）を知らせることと、 処理の結果出てきた別のデータ（return 式;によって返されてくる戻り値）を受け取ることが、呼び出す側の処理の全てだ。 そのあとで、受け取った値をどのように使うか（変数に代入したり、式の中で使ったり、printf()で表示したり・・・）は、呼び出し側の仕事になる。

つまり、関数をデザインするということは、このような「下請け会社」を設けることに相当し、関数の呼び出しとは、 必要なデータを渡した上で、下請け会社に仕事を発注し、結果を受け取る一連の作業と言えるだろう。 ある意味で、こうしたＣの関数は、ソフトウェアの部品とも言えるだろう 。

そして、複雑な仕事をどのような関数を使って（作って）分業させるか、が、Ｃプログラミングの重要なポイントとなる。

５．変数の見える範囲（スコープ）

ブロックの中の変数は、外からは見えない

C言語でブロック（{何々;}）は、複数の文をひとまとめにする以外に、もうひとつの重要な働きをする。 それは、変数の管理である。 これまでの例題では、変数宣言は関数定義の冒頭箇所に記述していた。 けれども、Ｃ言語のルールでは、ブロックの先頭箇所だったら、どこで変数宣言しても構わない。 例えば、次のような記述が可能である：

{
  int x=0,y=2 ;
  {
    int x=1 ;
    print("%d %d\n",x,y) ;
  }
}

これを実行すると、画面には"1 2"が表示される。 このとき、内側のブロックで宣言されている変数xと、外側で宣言されている変数xは（名前はたまたま同じであっても）別の箱（メモリー）になる。 そして、内側のブロックからは、その同じブロック内（内側のx）と、それより外側のブロックで宣言された変数（この例ではy）のみが「見える」。 また、ブロックの外側と内側に同じ名前の変数が宣言されている場合は、内側の変数のほうが見える。

このように、ブロックは、変数の見通せる範囲の「仕切り」としての役割も果たしているのだ。 もしこの機能が無ければ、大きなプログラムで、変数の「衝突」が生じてしまうだろう。 i,jといったよく使いそうな名前の変数が、プログラムの別の箇所でも使われていて、気づかないうちに 値が書き換わってしまうようなことがあったら、長いプログラムはとても記述できない。

Ｃの関数も（名前付きの）ブロックの一種であるから、ある関数の中から、別の関数の中で使われている変数は「見えない」し、 直接アクセスすることもできない。 このように、変数がどの範囲まで「見える」か、を、変数のスコープと呼ぶ。

グローバル変数

ある程度複雑なプログラムを書いていると、どの関数からも見える（アクセスできる）、共通的な変数があると便利なことが多い。 「同じブロックか、その外側が見える」というルールを思い出すと、どこからでも見える変数を設けるには、全てのブロックの外側で変数を宣言すれば良さそうだ。 事実、そうした記述は可能であって、

int global=1 ;
float data[1000] ;

main() {
  ・・・
}

func() {
  ・・・
}

のように、関数の「外側」でも変数宣言が可能だ。こうして宣言された変数は、全ての関数からアクセス可能なので、全体にわたる変数という意味で グローバル変数(global variable)と呼ぶ。 それとは対照に、関数やブロックの中だけで使われる変数を、ローカル変数（local variable）と呼ぶ。

　練習：素数を判定する関数

素数を引数に与えると 1, そうでない場合は 0 を返す、素数判定を行う関数 int is_prime(int n)をデザインし、 以下のひな形プログラムに書き加えて、正しく動作することを確認しなさい。

#include <stdio.h>
int is_prime(int) ;
main( )
{
    int n ;
    setbuf(stdout,NULL) ;
    for (n=3 ; n<=1000 ; n=n+1) {
        if (is_prime(n)==1) printf("%d ",n) ;
    }
    printf("\n") ;
}

/* 以下、is_prime() 関数の定義を追加する */

　ヒント

素数の判定アルゴリズムについては、多重ループ処理のページを参照のこと。

亀場で練習：素数の分布図

亀場を100×100のマス目に区切って、右上隅のマスが1、続いて、横に2, 3, 4, ・・・、そして、右下隅が10000を表すとしよう。 そのとき、素数を表すマス目だけに色を付け、下図のように1〜10000の素数の分布を可視化するプログラムを作成しなさい。

　ヒント

素数の判定には、ひとつ前の演習課題で作成した関数（int is_prime(int)）が使えるはず。

マス目を埋めるには、その場所に四角形として描いても良いが、（四角い）点を打ったほうが高速に描画できる。 POINT()関数を使って点線を描くプログラム例を以下に示す：

#include "turtle.h"
main()
{
	int i ;
	CON("localhost") ;
	CLR() ;
	JUMP(-256, 0) ; EAST() ;
	LW(16) ;  /* 点の大きさを16に設定 */
	POINT() ;  /* 点を打つモードに切り替える */
	for (i=0; i<32; i=i+1) {
		if (i%2==0) { PD() ; PU() ;} /* iが偶数の時に、現在位置に点を打つ */
		FD(16) ;
	}
}

$n$が十分に大きな数のとき、$n$以下の素数の数は$n/\log(n)$個程度であることが分かっている（素数定理）。 つまり、素数の密度はゆっくりと減少する。得られたプロットからその様子（気配？）が観察できるだろうか。