情報基礎A 「Cプログラミング」(ステップ9・ポインター・応用編)
このページでは、ポインターを用いたCコードの実例をいくつか学ぶ。(書きかけ)
1.多次元配列の動的確保
数値計算などを行なう際に、多次元の配列がしばしば必要になる。そして、そのサイズがあらかじめ決められないこともよくある。
そんなとき、例えば、変数n,mの値に応じて
float x[n][m] ;
* ただし、Cの処理系によっては動的確保(可変長配列)が可能なものもある
としたいところだが、このような配列の宣言はC言語では許されていない(配列のサイズは定数で指定しなければならない)*。 そこで、ポインタの出番となる。
2次元の配列は、1次元の配列を集めたもの、と見なすことができる。 上の例では、float型の要素数mの配列を単位として、それがn個、と考えればよい(下図):
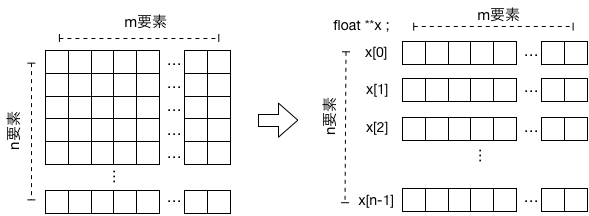
すると、float型の1次元配列n個分の先頭のアドレスを扱わねば(管理せねば)ならない。
そこで、そのアドレスを入れるためのn個の「箱」(1次元配列)を
float *x[n] ;と宣言したいところだ。
けれども、このような可変長(nが変数)の配列宣言がそもそも許されないから、こうやって思案しているのであった。
標準的なC言語には、一次元的な(連続した)メモリ領域を確保する方法が別に用意されており、
malloc(バイト数)は、指定したバイト数の連続したメモリ領域を確保し、戻り値として、その領域の先頭アドレスを返す。
システムのメモリがもう一杯になってしまった等の理由でメモリ確保に失敗するとNULL(ヌル・ポインタ)が返される。
sizeof(float *)は、floatへのポインタのサイズを表す。
#include <stdlib.h> ... float **x ; x = (float **) malloc(sizeof(float *)*n) ;
と記述すればよい。float型変数へのポインタのポインタ(ポインタの配列)変数xを宣言し、
malloc()で、float型のポインタ変数n個分の領域を確保する。
すると一次元配列x[0],x[1],...の各要素に、float型へのポインタ(つまりfloat型のデータが格納されている先のアドレス)を記憶することが可能となる。
次に、サイズmのfloat型の一次元配列のメモリ領域をn個分確保して、それぞれの先頭アドレスをx[0],x[1],...に順にセットすれば良い:
#include <stdlib.h>
float **x ;
int n,m ;
x = (float **) malloc(sizeof(float *)*n) ;
for (i=0 ; i<n ; i=i+1) {
x[i] = (float *) malloc(sizeof(float)*m) ;
}
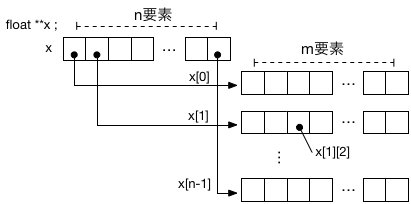
これによって、x[i][j]のようにして、配列の各要素にアクセスできるようになる。
C言語で、変数名[整数値]は、『変数の先頭から、その変数のサイズを単位に・・番目の内容』を表す。
よって、x[i][j]は、『xのi番目のアドレス(x[i])を先頭に、そこからj番目の箱の内容』、と処理系は解釈するわけである。
プログラムが終了すると、malloc()で確保した領域は自動的に解放される。
しかし、プログラム中でメモリ確保を繰り返すようなコードの場合、不要になった領域はその都度解放しておかないと、
システムのメモリを消費し尽くしてしまう。
このような状態をメモリリークと呼び、Cプログラムで生じ得る典型的な不具合のひとつである。
そのため、現代的なプログラミング言語は、メモリの確保と解放を処理系が自動的に行なう仕組み(ガーベージコレクション)を内蔵している例も多い(例えばJava等)。
こうして確保したメモリが不要になったら、free()によって解放(OSに返納)しておく。
以下の例に示すように、解放は、確保と逆順に行なう必要がある:
#include <stdlib.h>
for (i=0 ; i<n ; i=i+1) {
free(x[i]) ;
}
free(x) ;
以下のコードは、特に意味のある計算をするものではないが、動的に2次元配列を確保、関数に渡して計算を行なった後、メモリを解放する一連の流れを示す例として挙げておく:
#include <stdio.h>
#include <stdlib.h>
void func(int n, int m, float *x[]) {
int i,j ;
for (i=0; i<n ; i=i+1) {
for (j=0; j<m ; j=j+1) {
x[i][j] = i+j ;
}
}
}
main()
{
float **x ;
int n,m ;
int i ;
printf("nとmの値:") ;
scanf("%d%d",&n,&m) ;
x = (float **) malloc(sizeof(float *) * n) ;
if (x==NULL) {
fprintf(stderr,"メモリ確保に失敗しました\n") ;
exit(0) ;
}
for (i=0 ; i<n ; i=i+1) {
x[i] = (float *) malloc(sizeof(float) * m) ;
if (x[i]==NULL) {
fprintf(stderr,"メモリ確保に失敗しました\n") ;
exit(0) ;
}
}
func(n,m,x) ;
for (i=0 ; i<n ; i=i+1) {
free(x[i]) ;
}
free(x) ;
}
配列のサイズが大きくなると、上記のコードではいささか効率が悪くなってしまう。メモリを確保する都度、malloc(), free()をn回も呼ばなければならないからだ。そこで、連続したメモリ領域を一度に確保するよう変更したコードの例を示す:
連続した領域を一括して確保し、malloc()呼び出しの回数を節約した例
#include <stdio.h>
#include <stdlib.h>
void func(int n, int m, float *x[]) {
int i,j ;
for (i=0; i<n ; i=i+1) {
for (j=0; j<m ; j=j+1) {
x[i][j] = i+j ;
}
}
}
main()
{
float **x,*w ;
int n,m ;
int i ;
printf("nとmの値:") ;
scanf("%d%d",&n,&m) ;
x = (float **) malloc(sizeof(float *) * n) ;
if (x==NULL) {
fprintf(stderr,"メモリ確保に失敗しました\n") ;
exit(0) ;
}
w = (float *) malloc(sizeof(float) * n * m) ;
if (w==NULL) {
fprintf(stderr,"メモリ確保に失敗しました\n") ;
exit(0) ;
}
for (i=0 ; i<n ; i=i+1) {
x[i] = w + m * i ;
}
func(n,m,x) ;
free(x) ;
free(w) ;
}
この例では、$n \times m$の領域を一括して確保し(その先頭アドレスをポインタwにセット)、
これとは別に確保したポインタの配列xに、wの先頭からm要素おきのアドレスをセットしている
(x[i] = w + m * i ;の箇所)。
こうすれば、2次元配列の場合、malloc(), free()をそれぞれ2回呼び出せば事足りる。
 練習:3次元配列の動的確保
練習:3次元配列の動的確保
上の二次元配列の例をひな形として、三次元配列を動的に確保し、解放するプログラムを作成しなさい。
 ヒント
ヒント
二次元配列へのポインタの配列を用意し、二次元配列の確保は、上のひな形を流用するのが良さそうだ。
2.グラフの表現
鉄道や航路・道路の路線、ウェブのリンクの構造、交友関係から、細胞内の代謝経路やタンパクの相互作用に至るまで、世の中のあらゆるところに複雑なネットワークが登場する。それを数学的に抽象化したのがグラフ(graph)である。 グラフについては、例えば、教科書の 4.3 最適な経路を探す(p.121)や付録A.4も参照のこと。
グラフは、頂点と、頂点間を結ぶ辺から構成される。その構造を表現する自然な方法のひとつが、隣接行列を用いる方法である。 頂点に順に番号を割当て($i=1,2,\cdots,n$)、頂点$i$から頂点$j$が辺で結ばれているときは$ a_{ij} = 1 $、そうでないときは $a_{ij}=0$ と置く。 このとき、隣接行列は $A=\{ a_{ij} \}$ で与えられる。
現実のネットワークは、他の頂点とほとんど繋がっていないことが多い。例えば、どんなに巨大なハブ空港であっても、接続があるのはごく限られた都市だけであるし、東京駅のような大きな駅でも、その隣の駅は、数えるほどしかない。つまり、隣接行列の要素は殆ど0ばかりになる。 加えて、ネットワークの構造や規模が時間と共に変化するようなケースも多く(例えば、インターネットのルーティングはその典型であろう)、隣接行列では扱いにくい(メモリー効率が悪い)。
そんな場合は、頂点とそこから伸びる辺のみを記憶する(繋がっていないところは記憶しない)ようなデータ表現が適している:
頂点についてのデータ:
名前(または番号)
隣接する頂点のリスト(配列)
複数の属性がセットになって、ある情報を表すことはよくある。
そのような場合、構造体を使うと、自然にアルゴリズムをコーディングできる。
関連するC言語の文法やルールについては、
構造体(struct)、
共用体(union)、
ビットフィールド(bit field)、
構造体へのポンタ−、
構造体の配列、
等をキーワードに、
さらに調べることを勧めたい。
これをC言語流に、構造体を使って表現すると、
struct vertex {
char *name ;
struct vertex **link ;
} ;
と書くことができる。構造体の各項目はメンバーと呼ぶ。このように構造体を宣言すると、新たに struct vertex というデータ型を持った変数を宣言し、操作できるようになる:
struct vertex x ; /* 構造体変数xの宣言 */ struct vertex * p ; /* 構造体変数へのポインタpの宣言 */ p = &x ; /* 構造体変数xのアドレスをpに代入 */ x.name = NULL ; /* xのメンバーnameに NULL(ヌルポインタ)を代入 */ p->link = NULL ; /* pがポイントしている構造体変数のメンバーlinkにNULLを代入 */
この構造体(struct vertex)を使って、頂点の作成(create_vertex() )、
辺(隣接する頂点)の追加(add_vertex())、
頂点の接続(connect_vertex())をCでコーディングした例を以下に示す。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct vertex {
char *name ;
int max_adj ;
struct vertex **link ;
} ;
struct vertex * create_vertex(char *name)
{
struct vertex *v ;
v = (struct vertex *) malloc(sizeof(struct vertex)) ;
v->name = (char *) malloc(sizeof(strlen(name))+1) ;
strcpy(v->name,name) ;
v->max_adj = 2 ;
v->link = (struct vertex **) malloc(sizeof(struct vertex *)*(v->max_adj + 1)) ;
v->link[0] = NULL ;
return v ;
}
void add_vertex(struct vertex *v, struct vertex *a) {
int n=0 ;
while (v->link[n] != NULL) {
if (v->link[n] == a) return ;
n=n+1;
}
if (n >= v->max_adj) {
v->max_adj = v->max_adj*2 ;
v->link = (struct vertex **) realloc(v->link, sizeof(struct vertex *)*(v->max_adj+1)) ;
}
v->link[n] = a ; v->link[n+1] = NULL ;
}
void connect_vertex(struct vertex *v1, struct vertex *v2) {
add_vertex(v1,v2) ;
add_vertex(v2,v1) ;
}
void print_link(struct vertex *v)
{
int n=0 ;
printf("%s -> ",v->name) ;
while (v->link[n] != NULL) {
printf("%s ",(v->link[n])->name) ;
n=n+1;
}
printf("\n") ;
}
main()
{
struct vertex *v1,*v2,*v3 ;
v1 = create_vertex("tokyo") ;
v2 = create_vertex("kanda") ;
v3 = create_vertex("yurakucho") ;
connect_vertex(v1,v2) ;
connect_vertex(v1,v3) ;
print_link(v1) ;
}
補足説明:
上の例では、構造体のメンバーにint max_adj ;を加え て、リスト(.link)に登録できる最大の辺(隣接する頂点)の数を管理するようにした。
その初期値は2で、辺を追加して足りなくなると、2倍に増やすようになっている。
add_vertex()の中で使われているrealloc(ポインター, 新しいサイズ)関数は、確保済みのメモリー領域のサイズを変更し、新たなメモリーを割り当てる(もともと保存されていたデータはコピーされ、引き継がれる)。
辺のリストのためのメモリが足りなくなると、サイズを倍にして、メモリ領域を確保し直してる。
隣接する頂点のリスト(構造体のメンバーlink)は、項目の末尾の印として、NULL(ヌルポインター)を使っている。NULLは、プログラムで使われるメモリ領域の「外」の特別な場所(0番地)を意味する。
構造体へのポインターを v とすると、v->メンバー名によって、そのメンバーにアクセスできる。v->nameは、(*v).nameと同じ意味である。
 練習:ランダムなネットワークの自動生成
練習:ランダムなネットワークの自動生成
上のプログラムをひな形として、頂点数が$N$で、各頂点が$M$本の辺を持つようなグラフを生成するコードを書きなさい。 $M$本の辺は、ペアとなる頂点がランダムに選ばれるように工夫しなさい。 こうして生成されたグラフ(ネットワーク)は、Erdős–Rényi modelとしてよく調べられている。
 ヒント
ヒント
$0$から$N-1$までの乱数(整数)を生成するには random()%N を用いるとよい。
ある頂点の現在の辺の数を調べる関数をコーディングした例を示す:
int n_edge(struct vertex *v)
{
int n=0 ;
while (v->link[n] != NULL) {
n=n+1;
}
return n ;
}