情報基礎A 「Cプログラミング」(ステップ7・配列・基本)
このステップの目標
- 配列変数を用い、配列要素への適正なアクセスに配慮したプログラムが書ける
- 計算によってアクセス位置を変えたり、配列要素の並べ替え操作を伴う処理、および必要なデータを探索するアルゴリズムを理解できる
1.配列変数の基本
コンピュータを使って大量のデータを処理するために必須の機能のひとつ、それが配列だ。 「プログラミングの入門編」といえども、この配列は是非マスターしておきたい。
 配列変数:沢山のメモリー(変数)を一括して確保し、通し番号でアクセスする
配列変数:沢山のメモリー(変数)を一括して確保し、通し番号でアクセスする
これまで書いてきたプログラムでは、変数が必要になったら、その都度、名前を付けて、
int a ; float x ;
のように宣言していた。 ところが、例えば、1000人から成る集団があって、それぞれの情報(例えば体重)を使った処理をしたいような場合、同じような変数宣言を1000回も書くのは御免こうむりたい。 このように、データの件数が多い場合(あるいは、データの件数が不定の場合)には、必要な個数のメモリを一括して宣言し、それぞれを通し番号(**番目)で管理するのが理にかなっている。
C言語に限らず、一般のプログラミング言語では、こうした用途に使うために、配列型のデータ構造(array data type)が用意されている。
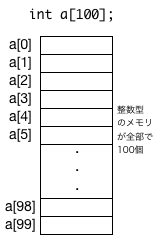
例えば、int型の変数を100個、float型の変数を1000個分、一括して準備したい場合は、
int a[100] ; float x[1000] ;
のように宣言する。括弧[ ]の中には、必要な変数の個数を記述する。
配列変数へのアクセス
これらの変数の中身(データ)には、通し番号(添字, index)を付け、要素ごとにアクセスする。例えば、
a[3] = 17 ; x[i] = x[i-1] + x[i+1] - 2 * x[i] ;
のように。つまり [ ] の中に、何番目のハコであるかを指定するわけだ。 ハコの場所は、整数値で指定しても良いし、変数や数式であっても構わない。
配列へのアクセスの「はみ出し」は、コンパイル時には検出できないので、とても厄介だ。
ここで、気をつけなければならないのは、通し番号(添字)は0から始まることだ。
100個の要素から成る配列を宣言したら、おしまいの要素の番号は99である(図参照)
あらかじめ宣言した範囲を超えた要素(例えば a[-1]やa[100])にアクセスすると、
プログラムは『予期せぬ動作』をするので、十分注意すること。
配列データのコピー
標準的なCの処理系には、連続したデータをコピーするためmemcpy()関数等が用意されており、
実際のプログラミングではそちらを使う場合も多い。
配列変数の中身をそっくりコピーする場合、
int a[100],b[100] ; ・・・ a = b ;
のように書いてはいけない。「配列へのアクセスは要素ごとに行う」のが基本ルールである。 であるから、面倒だけれども、
int a[100],b[100] ; int i ; ・・・ for (i=0; i<100; i=i+1) a[i] = b[i] ;
のように、反復処理を使って、要素毎に逐一代入する必要がある。
2. 配列へのアクセスと操作
配列変数を使うと、アクセスする場所(添字の値)を変数や式を使って指定することで、様々なデータの処理や加工が可能となる。
次の例題は、配列中のデータを、ひとつ「右」(添字が大きい位置)にずらし、一番「右」のデータは、 一番「左」に移動(つまりデータの位置を右向きにシフト、あるいは回転)し、結果を表示するCコードの例である。
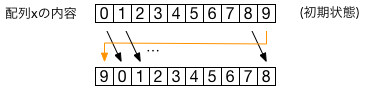
例題8a(ex8a.c)
配列中のデータのシフト
![]()
#include <stdio.h>
#define N 10
main( )
{
int x[N] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } ;
int i,t ;
t = x[N-1] ;
for (i=N-1 ; i>0 ; i=i-1) {
x[i] = x[i-1] ;
}
x[0] = t ;
for (i=0 ; i<N ; i=i+1) {
printf("%d番目の値= %d\n",i,x[i]) ;
}
}
プログラムの見所
forループで変数 i を「カウントダウン」方式で操作している理由、変数 t が必要な理由をよく考えてみるとよい。
#define N 10
このページの例題プログラムでは、宣言部に #define N 10 とある。
これは、『これ以降では N と書いたら、それは 10 と書いたことと見なす(Nを10と定義する)』という宣言である。
したがって、in x[N] は int x[10] を、for (i=0;i<N;i=i+1)はfor (i=0;i<10;i=i+1)を、それぞれ意味する。
このNは変数ではないので注意すること。
配列変数の初期化
配列変数の初期値を設定する場合に、いちいち、
x[0] = 0 ; x[1] = 1 ;
のように書くのは手間がかかるので、上記の例のように、まとめて
のような書き方が許されている。ただし、この 配列[ ]={ }; の記法は変数宣言の際にだけ(最初の1回だけ)使うことができる。
 練習:配列の要素のシフト
練習:配列の要素のシフト
例題8aをもとにして、配列xのデータを「左」にシフトし、結果を表示するプログラムを書きなさい。
 練習:配列の内容の反転
練習:配列の内容の反転
以下に示すひな形をもとに、配列xの要素の並び順を逆転させた上で出力するプログラムを書きなさい。
ひな形
#include <stdio.h>
main()
{
int x[10]={9,8,7,6,5,4,3,2,1,0} ;
int i,t ;
?????
?????
?????
for (i=0 ; i<10 ; i=i+1) {
printf("%d番目の要素=%d\n",i,x[i]) ;
}
}
|
 ヒント
ヒント
入れ替えのアルゴリズムは、N枚のカードの並べ替えですでに考察済みである。
i番目の配列要素と入れ替えを行うべき要素の位置を i を使った式でどのように表せばよいか、添字の範囲に注意して、よく考えること。
 練習:あみだくじ
練習:あみだくじ
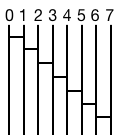
左図のあみだくじの「行き先」を求めるCプログラムを書いてみなさい。反復処理を使うこと。結果は
0 -> 7 1 -> 0 2 -> 1 ...
のように出力すること。
 ヒント
ヒント
i 番目の縦棒の行き先を x[i] の値で表現してはどうか? その上で、あみだくじを、配列データの「入れ替え」操作として捉え直すと良い。 入れ替えの順序も重要である。
ひな形
#include <stdio.h>
#define N 8
main()
{
int x[N]={0,1,2,3,4,5,6,7} ;
int i,t ;
?????
?????
?????
for (i=0 ; i<N ; i=i+1) {
printf("%d -> %d\n",i,x[i]) ;
}
}
|
3.配列内のデータの検索
データの中から必要なものを探し出すのは、情報を扱う上での基本である。 そして、我々はコンピュータを使って、膨大なデータの検索を、日常的に行っている。 この節では、配列を一種のデータベースに見立てて、情報の探索のいくつかの基本パターンを紹介する。
データの検索(線形探索)
例題8b(ex8b.c)
配列中の中から特定の値のデータを見つける
#include <stdio.h>
#define N 10
main( )
{
int x[N] = { 12, 11, 9, 13, 8, 4, 3, 5, 6, 1 } ;
int i,k,n ;
printf("検索する数: ") ;
scanf("%d",&n) ;
k=-1 ;
for (i=0 ; i<N ; i=i+1) {
if (x[i]==n) {
k = i ;
break ;
}
}
if (k<0) {
printf("その数は見つかりません\n") ;
} else {
printf("その数は %d 番目の位置に見つかりました\n",k) ;
}
}
プログラムの見所
変数kを最初に-1にセットしておき、配列中に入力した数値が見つかったら、その添字をkに代入しforループを抜けている。そうすると、もしkが初期値のまま(-1)であれば、 if (x[i]==n)の判定が「真」とはならなかった、つまり、その数が見つからなかったことになる。もしkが0以上なら、それはデータの位置(添字の値)になっている。
最大値・最小値
数値計算や、統計処理などを行う際に、配列中のデータの中で一番大きな値が必要になることがよくある。 以下は、配列中の最大値を見つけるプログラムの例である。
例題8c(ex8c.c)
配列中のデータの中から最大値を探し出す。
#include <stdio.h>
#define N 10
main( )
{
float x[N] = { 2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8 } ;
int i ;
float maxval ;
maxval = x[0] ;
for (i=1 ; i<N ; i=i+1) {
if (x[i] > maxval) {
maxval = x[i] ;
}
}
printf ("最大値= %f\n",maxval) ;
}
プログラムの見所
配列データの中から最大値を探す手順
8行目から16行目にかけてが配列の中から最大値を見つける処理で、アルゴリズムをまとめると:
1: 仮の最大値として、最初の要素の値を設定する(仮の最大値は、本当の最大値を超えない値ならば何でも良い) 2: 配列の中身を順に最後まで調べる: 3: もし、i番目の値が、仮の最大値より大きければ、仮の最大値としてi番目の値をセットする 4: この時点での、仮の最大値を、配列全体を通しての最大値とする
上の手順をちょっとだけ変更すれば、最小値を見つけるアルゴリズムになる。
整列済みのデータ内からの探索(二分探索)
配列データの中に、ある値を持ったデータが含まれているかどうかを調べるには、添字を0から順に変えながら値を比較すればよい(線形探索)が、 データの件数が膨大になると、無視できない手間となる。 けれども、もしデータが既に(ここでは昇順に)整列済みの場合は、二分探索法(binary search algorithm)と呼ばれる、 シンプルながらも効率的なアルゴリズムが利用できる。
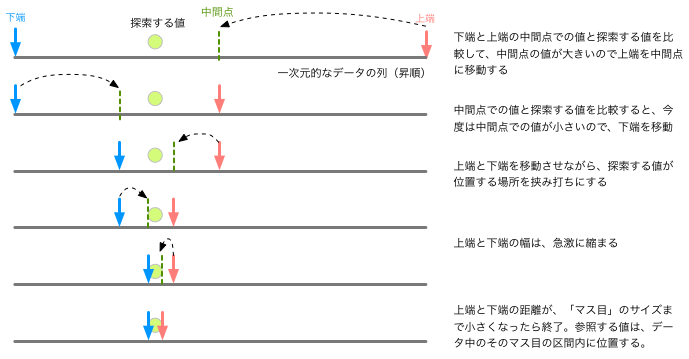
以下は、この二分探索を使って、キーボードから入力した数値が、配列xの中のどの区間(何番目の要素の間)に位置するかを調べ、表示するCプログラムの例である。 入力値を$v$とすると、$x_i \le v \lt x_{i+1}$ となるような $i, i+1$ が出力される。 このプログラムでは、N=10 件の既に昇順に整列済みの配列データを用いており、 データの最小値よりも小さい$v$を入力すると [-1,0] が、最大値より大きな$v$については [N-1, N] が出力される。
例題8d(ex8d.c)
二分探索
#include <stdio.h>
#define N 10
main( )
{
float x[N] = { 1.2, 2.1, 3.1, 4.7, 4.8, 5.3, 5.3, 7.3, 8.3, 9.2 } ;
int i,il,ih ;
float val ;
printf("探したい値:") ;
scanf("%f",&val) ;
il=-1 ;
ih=N ;
for (;;) {
if (ih-il<=1) break ;
i = (ih + il)/2 ;
if (x[i]<=val) il=i ;
else ih=i ;
}
printf ("そのデータは %d 番目と %d 番目の要素の間に位置します\n",il,ih) ;
}
例題8d「二分探索」のアルゴリズム
Input: 10件のデータが昇順に入った配列 $\{x_i\}$ と探索する値 $v$
Output: $x_{i} \le v \lt x_{i+1}$となるような $i, i+1$の組
1: 配列$\{x_i\}$に10件のデータをセットする
2: キーボードから値を$v$にセットする
3: 下端の位置を $i_l \leftarrow -1$ とする
4: 上端の位置を $i_h \leftarrow 10$
5: 下端と上端が接する($i_h - i_l \le 1$ となる)まで、9: までを繰り返す
6: 下端と上端の中間位置を $i$ にセットする( $i \leftarrow (i_h + i_l)/2$ )
7: もしも $x_i \lt v$ ならば、$i$を新しい下端とする($i_l \leftarrow i$)
8: そうでなければ、$i$を新しい上端とする($i_l \leftarrow i$)
9: 反復ここまで
10: 上端と下端の位置を出力する
11: 終了する
プログラムの見所
forループの箇所がこのコードの中心部分で、
変数ilを下端、ihを上端として、その中間位置i=(il+ih)/2での配列の値とデータを比較し、
その大小関係に応じて、下端または上端の位置を更新している。
いわば、『挟み打ち』にする作戦である(下図)。
地下に埋設されたケーブルのどこかに不具合があったとき、全体を掘り返す代わりに、まず問題のある区間の中間点を掘ってみて、 問題箇所がその上流側が下流側かを調べ、調べる区間を狭める。 こうした作業を繰り返せば、短時間で問題箇所を特定できるはずである。
 練習:最小値
練習:最小値
配列データ中の最大値を見つけるプログラム(例題 8c)を修正し、最小値を見つけ、出力するコードを作成しなさい。
 練習:線形探索
練習:線形探索
二分探索のアルゴリズムを使った例題8dは高速ではあるが、プログラムの動作を理解するのは少し慣れが必要かもしれない。
この課題では、最もシンプルなアルゴリズムである線形探索(配列の先頭から順にひとつずつ要素を調べるやり方)によって、入力した値が(以下に示すひな形コードの)昇順に並んだ配列中のデータのどの区間に属するかを探索する(例題8dと同様の動作をする)プログラムを作成してみなさい。
 ヒント
ヒント
例えば、3.5 に対して x[2] <= 3.5 < x[3] が成り立つから、「3.5 は 2番目と3番目の要素の間に位置」する。
さらに一般に、x[i] <= val < x[i+1] が成立していれば、「val は i 番目と i+1 番目の要素の間に位置」となるだろう。
ひな形
#include <stdio.h>
#define N 10
main( )
{
float x[N] = { 1.2, 2.1, 3.1, 4.7, 4.8, 5.3, 5.3, 7.3, 8.3, 9.2 } ;
int i,il,ih ;
float val ;
printf("探したい値:") ;
scanf("%f",&val) ;
for (??? ; ??? ; ???) {
????
????
}
printf ("そのデータは %d 番目と %d 番目の要素の間に位置します\n",il,ih) ;
}
|
 練習:データのカウント
練習:データのカウント
以下のひな形をもとに、与えられた配列(x)中に、指定した範囲(上限、下限も含む)にあるデータが何個含まれるかをカウントして、結果を出力するプログラムを作成しなさい。
例えば、下限値1、上限値3を検索すると6個、下限値7、上限値10を検索すると2個、と出力するようにしなさい。
ひな形
#include <stdio.h>
#define N 10
main( )
{
float x[N] = { 3, 1, 0, 1, 8, 1, 2, 3, 9, 4 } ;
float minval, maxval ;
int i, count ;
printf("下限値:") ;
scanf("%f",&minval) ;
printf("上限値:") ;
scanf("%f",&maxval) ;
?????
for (??? ; ??? ; ???) {
????
????
}
printf ("その範囲のデータが %d 個見つかりました\n",count) ;
}
|
 練習:フィボナッチ数列
練習:フィボナッチ数列
フィボナッチ数列は、初項を $x_0 = 1, x_1 = 1$ として、漸化式 $x_n = x_{n-1} + x_{n-2}$ $(n \ge 2)$ によって計算される数列で、数理的な問題や自然現象、造形物など、 色々な事象と関わることで良く知られている。 具体的には、1, 1, 2, 3, 5, 8, 13, 21, ... と単調に(しかも急激に)値が増大する数列となる。
以下のひな形をもとにして、配列の i 番目の要素に順に $x_i$ をセットし、$x_{29}$ までの値を出力するCプログラムを作成しなさい。

ひな形
#include <stdio.h>
#define N 30
main()
{
int x[N] ;
int i ;
????
...
/* xの内容を出力 */
for (i=0 ; i<N ; i=i+1) {
printf("x[%d]= %d\n",i,x[i]) ;
}
}
|
 亀場で練習:フィボナッチの正方形列
亀場で練習:フィボナッチの正方形列
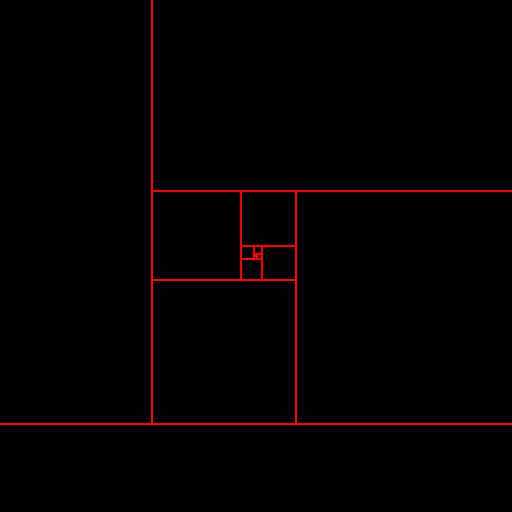
下図は、一辺の長さがフィボナッチ数列になるような大きさの正方形を並べて描いたものである。 漸化式 $x_n = x_{n-1} + x_{n-2}$ から、「2つ前までの正方形の辺の長さの和が、ちょうど次の正方形の辺の長さになる」ような関係が成り立っている。 原点(中央)から描画を開始し、図のようなパターンを描くプログラムを作成しなさい。
フィボナッチ数列の計算部分は、ひとつ上の練習問題のコード使うと良い。
図
 ヒント
ヒント
少し「無駄足」になってしまうが、正方形を描く際に、同じ場所を再びなぞることで、一筆書きで描くことができるはずだ(下図)。
この図形に関係して、Golden spiral についても調べてみるとよい。