情報基礎A 「Cプログラミング」(ステップ7・最小二乗法・計算編)
このページでは、配列を用いた統計計算の例として、回帰直線をCプログラムで計算する方法について考える。
二つの量をペアとして表現する
二次元配列を使わず、2つの一次元配列(例えば、float x[ ], y[ ] ;)でデータを表現することも出来るが、
ここでは、対応関係をより意識したコーディング・スタイルを選んだ。
実験などで二つの量の関係を調べるケースは多い(というよりは、殆どがそうなので、敢えて例を挙げるまでもないだろう)。 ここでは、$X$という量を変えながら、$Y$という量を調べている、という場合を想定しよう。
そのように、組になったデータを扱う際には、C言語の二次元配列を用いると、すっきりとコーディングできる。 例えば、$(x,y)$ が12ペアあるようなデータを表現するには、
float x_vs_y[12][2] = {{1,1.9},{2,1.4},{3,5.5},{4,10.9},{5,16.5},{6,20.6},
{7,23.7},{8,24.6},{9,20.5},{10,15.3},{11,10.0},{12,2.8}} ;
これはfloat型の2次元配列 x_vs_y を宣言した例で、2つずつの値が、合計12セット、初期値として代入されている。 この場合、配列の要素数12は省略できて
float x_vs_y[][2] = {{1,1.9},{2,1.4},{3,5.5},{4,10.9},{5,16.5},{6,20.6},
{7,23.7},{8,24.6},{9,20.5},{10,15.3},{11,10.0},{12,2.8}} ;
多次元配列の初期化を伴った宣言の際に、要素数を省略できるのは、一番「左側」の要素のみ。
と書いても構わない(12のところは、コンパイラーが自動的に計算して補ってくれる)。
ただし[2]の2を省略することはできない。
二次元配列は、数学の行列のイメージと対応する。 上の例は、$(x,y)$ で構成される行ベクトルを12個縦に並べたもの、と考えると良い: $$ \left( \begin{array}{cc} 1 & 1.9 \\ 2 & 1.4 \\ 3 & 5.5 \\ 4 & 10.9 \\ \vdots & \vdots \end{array} \right) $$
そして、C言語では配列の要素が0から始まることを思い出すと、
この例では、x_vs_y[0][0]には1、x_vs_y[0][1]には1.9が記憶されている。
x_vs_y[2][1]は、5.5 ということになる。
プログラムの中でデータをセットするには、例えば、以下のようにコーディングすれば良い:
float x_vs_y[12][2] ;
....
for (i=0; i<12 ; i=i+1) {
x_vs_y[i][0] = (i番目のXの値) ;
x_vs_y[i][1] = (i番目のYの値) ;
}
量の関係を回帰直線によって特徴付ける
以下では、量 $X$ については、きちんと値が確定できるが、$Y$については、 測定の度に対象側の事情で値が揺らいだり、測定そのものに不定性(誤差)があるような組み合わせを考える。 例えば、$X$は細胞に照射された放射線量、$Y$は細胞の生存数、などを想像してみるとよい。
最小二乗法の解説
データを正しく解釈するには、「考え方」も大切である。
例えば、最小二乗法で得られる回帰直線は、感覚的に「データ点の丁度ど真ん中あたりに引いた直線」になるとは限らない。
$X$の変化が$Y$に及ぼす影響が、揺らぎや誤差を別とすれば、直線的であることが期待されるとき、 その様子を特徴付ける方法として、最小二乗法による直線回帰が広く用いられる。 その考え方と「公式」の導出方法については、理論編のページにまとめておいたので、そちらを参照すること。
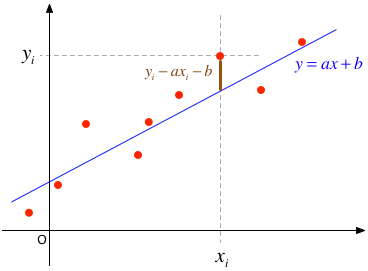
データが全部で$n$点あり、$i$番目の$X$の値を$x_i$、$Y$の値を$y_i$と表記することにする。 ここではC言語の流儀に従って、$i=0,1,2,\cdots,n-1$とする。 このデータ集合を「もっとも良く表す」ような直線(回帰直線) $y = a x + b$ の傾き $a$ と切片 $b$ は、 データから得られる統計量を使って、以下の手順で求めることができる:
$E(X)$は「$X$についての期待値(expected value)」の意味。
CのプログラムでこれをそのままE(X)と書くと、「関数EにXを渡して呼び出す」と解釈されるので、
変数名としては、例えば、e_xなどとするのが良いだろう。
【ステップ1】データ $(x_i,y_i)$ について、以下の平均量を計算する: $$ E(X) = \frac{1}{n} \sum_{i=0}^{n-1} x_i ,\\ E(XX) = \frac{1}{n} \sum_{i=0}^{n-1} {x_i}^2 ,\\ E(XY) = \frac{1}{n} \sum_{i=0}^{n-1} x_i y_i ,\\ E(Y) = \frac{1}{n} \sum_{i=0}^{n-1}y_i $$
【ステップ2】こうして求めた $E(X), E(XX), E(XY), E(Y)$ を用いると、$a, b$ の値は公式 $$ a = \frac{E(XY) - E(X) E(Y)}{E(XX) - E(X)^2} ,\\ b = \frac{E(XX) E(Y) - E(XY) E(X)}{E(XX) - E(X)^2} $$ から得られる。
こうして直線の傾き $a$ と切片 $b$ を決めると、データ点と直線とのy軸方向の残差の二乗和 $$ \sum_{i=0}^{n-1} \left( y_i - a x_i - b \right)^2 $$ を最小とすることができる。
 練習:地球の気温のトレンド
練習:地球の気温のトレンド
以下は、University of East Angliaのグループが公開しているデータを元に、 1850年から2014年までの地球上(地上)の気温の変動(各地の平均気温からの変動分)をCの配列として定義したものである。 これを用い、 時間(西暦年)を$X$、気温変動(temperature anomaly(度))を$Y$として、回帰直線 $y=ax+b$ のパラメータ $a,b$ を計算・表示するCプログラムを作成せよ。
この期間、10年あたりに換算して、地球上の気温は平均的に何度変化したと考えられるか?
float year_vs_temp[][2] = {
{1850,-0.425},{1851,-0.011},{1852,-0.208},{1853,-0.398},{1854,0.131},
{1855,-0.111},{1856,-0.369},{1857,-0.247},{1858,-0.401},{1859,-0.265},
{1860,-0.354},{1861,-0.300},{1862,-0.590},{1863,-0.334},{1864,-0.631},
{1865,-0.295},{1866,-0.359},{1867,-0.384},{1868,-0.316},{1869,-0.272},
{1870,-0.292},{1871,-0.422},{1872,-0.165},{1873,-0.233},{1874,-0.392},
{1875,-0.606},{1876,-0.260},{1877,-0.069},{1878,0.101},{1879,-0.402},
{1880,-0.164},{1881,-0.311},{1882,-0.134},{1883,-0.417},{1884,-0.543},
{1885,-0.504},{1886,-0.421},{1887,-0.517},{1888,-0.485},{1889,-0.239},
{1890,-0.472},{1891,-0.585},{1892,-0.596},{1893,-0.690},{1894,-0.547},
{1895,-0.558},{1896,-0.380},{1897,-0.299},{1898,-0.395},{1899,-0.329},
{1900,-0.170},{1901,-0.182},{1902,-0.355},{1903,-0.429},{1904,-0.571},
{1905,-0.440},{1906,-0.226},{1907,-0.615},{1908,-0.488},{1909,-0.464},
{1910,-0.342},{1911,-0.461},{1912,-0.388},{1913,-0.331},{1914,-0.066},
{1915,-0.076},{1916,-0.358},{1917,-0.693},{1918,-0.478},{1919,-0.255},
{1920,-0.303},{1921,-0.159},{1922,-0.261},{1923,-0.291},{1924,-0.375},
{1925,-0.285},{1926,-0.052},{1927,-0.235},{1928,-0.157},{1929,-0.439},
{1930,-0.139},{1931,-0.131},{1932,-0.070},{1933,-0.289},{1934,-0.068},
{1935,-0.171},{1936,-0.114},{1937,-0.068},{1938,0.110},{1939,-0.060},
{1940,-0.033},{1941,-0.015},{1942,-0.030},{1943,-0.072},{1944,0.082},
{1945,-0.110},{1946,-0.082},{1947,-0.021},{1948,-0.059},{1949,-0.148},
{1950,-0.320},{1951,-0.130},{1952,-0.039},{1953,0.058},{1954,-0.187},
{1955,-0.206},{1956,-0.433},{1957,-0.051},{1958,0.078},{1959,-0.011},
{1960,-0.100},{1961,0.043},{1962,0.001},{1963,0.006},{1964,-0.288},
{1965,-0.201},{1966,-0.122},{1967,-0.119},{1968,-0.211},{1969,-0.059},
{1970,-0.021},{1971,-0.204},{1972,-0.174},{1973,0.152},{1974,-0.303},
{1975,-0.115},{1976,-0.370},{1977,0.081},{1978,-0.050},{1979,0.063},
{1980,0.143},{1981,0.249},{1982,0.017},{1983,0.316},{1984,-0.058},
{1985,-0.008},{1986,0.117},{1987,0.287},{1988,0.348},{1989,0.199},
{1990,0.431},{1991,0.343},{1992,0.092},{1993,0.175},{1994,0.333},
{1995,0.468},{1996,0.204},{1997,0.463},{1998,0.820},{1999,0.489},
{2000,0.361},{2001,0.552},{2002,0.664},{2003,0.646},{2004,0.611},
{2005,0.747},{2006,0.669},{2007,0.678},{2008,0.528},{2009,0.642},
{2010,0.713},{2011,0.539},{2012,0.621},{2013,0.724},{2014,0.742}
};
 亀場で練習:グラフのプロット
亀場で練習:グラフのプロット
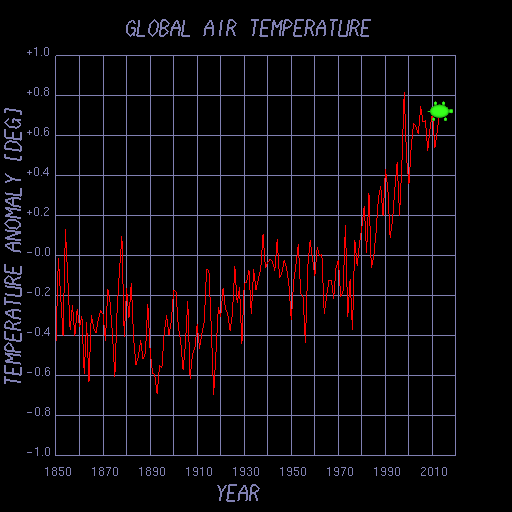
亀場を使って、西暦と気温の変動の関係のデータ(year_vs_temp)を、下図のようにプロットするプログラムを作成せよ。
加えて、最小二乗法で求めた回帰直線をグラフに重ねて描いてみよ。
亀場を使って描いたグラフの例
 ヒント
ヒント
亀場に英数字を描くにはSAY( )関数やTPRINTF( )が使える。
また、文字のサイズを変えたり、寝かせて描く場合は、簡易プロッターライブラリを使うとよい。