Cプログラミング(ステップ6・数値積分・DE法)
このページの目標
- 積分を効率的に精度よく見積もることができるDE法のアイデアを理解し、コードに反映できること。
無限区間の積分
ガウス関数は、両端が滑らかに0に漸近するので、中央の凸部とその両脇の凹部とで、台形近似で生じる「ずれ」(面積の過不足)をうまく相殺してくれる。
いろんな科目を学んでいると、ガウス積分 $$ I=\int_{-\infty}^{\infty} e^{-x^2} dx $$ の値が必要になることが多い。 このケースは簡単に積分できるし、あまりに一般的なので、特にプログラミングをせずとも色々な方法でその値を知ることができるが、 もし、数値積分を行うとすると、$\infty$をどのように扱えばよいかが悩ましい。 ところが、被積分関数 $e^{-x^2}$ は積分区間の両端で滑らかかつ急激に0になるので、これを 台形則で有限の積分区間で近似的に計算しても、 とてもよい結果が得られることが知られている。 以下のコードは、台形の幅をかなり粗目に$h=0.5$にとって、$[-10,10]$の区間で台形法の計算を行う例であるが、 「両端を1/2倍する処理」をさぼっているにもかかわらず、非常に正確な結果を得ることができる。
#include <stdio.h>
#include <math.h>
main()
{
float x,h=0.5;
float sum=0.0 ;
int i ;
for (i=-20 ; i<=20 ; i=i+1) {
x = i * h ;
sum = sum + exp(-x*x) ;
}
sum=sum*h ;
printf("I(台形法)= %f\n",sum) ;
printf("I(厳密値)= %f",sqrt(M_PI)) ;
}
有限区間の積分を無限区間で見積もる
今度は、有限区間の積分 $$ I = \int_a^b f(x) dx $$ を考える。 このとき、うまい変数変換 $x=\phi(t)$ があって、 $\lim_{t \to -\infty} \phi(t) = b$, $\lim_{t \to \infty} \phi(t) = a$ となっているとしよう。 すると、積分は $$ I = \int_{-\infty}^{\infty} f(\phi(t)) \frac{d\phi}{dt} dt $$ となる。もし $\frac{d \phi}{dt}$ が積分の両端で滑らか、かつ急激に、0に漸近するような性質を持てば、 これに台形法を適用することで、ガウス積分の例と同様、よい近似を得ることができるはずである。
$a=-1,\; b=1$の場合、 $$ \phi(t) = \tanh\left(\frac{\pi}{2} \sinh(t) \right) $$ がそのよい例であることが発見されている。その微分は $$ \frac{d\phi}{dt} = \frac{\frac{\pi}{2} \cosh(t)}{\cosh^2\left(\frac{\pi}{2}\sinh(t)\right)} $$ である。
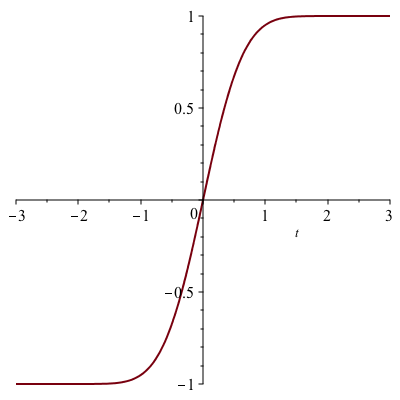
$\phi(t) = \tanh\left(\frac{\pi}{2} \sinh(t) \right)$のプロット: $t$の絶対値が大きいと急激に一定値($\pm 1$) に近づく。 このグラフからは、動かす$t$の範囲は、-3から3くらいまででも十分であることが伺える。
積分区間が$[a,b]$の場合は、 $$ x = \frac{b-a}{2} \phi(t) + \frac{a+b}{2} $$ と座標を取り直せばよい。つまり $$ I = \frac{b-a}{2} \int_{-\infty}^{\infty} f\left( \frac{b-a}{2} \phi(t) + \frac{a+b}{2} \right) \frac{d\phi}{dt} dt $$ となる。 このように変換を施し数値積分を行う方法は、$\phi$が二重に指数関数を組み合わされて構成されていることから、 DE(Double Exponential)公式と呼ばれている。
以下は、このアイデアをCのコードで表現し $$ \int_0^{\pi} \sin(x) dx = 2 $$ を数値的に評価する例である:
#include <stdio.h>
#include <math.h>
main()
{
float a=0;
float b=M_PI ;
float h=0.25 ;
float phi,dphidt ;
float x,t,s,sum ;
int i ;
sum=0.0 ;
for(i=-20 ; i<=20 ; i=i+1) {
t = i*h ;
s = (M_PI/2)*sinh(t) ;
phi = tanh(s) ;
dphidt = (M_PI/2)*cosh(t) / (cosh(s)*cosh(s)) ;
x = (b-a)*phi/2 + (b+a)/2 ;
sum = sum + sin(x) * dphidt ;
}
sum=(b-a)/2*sum*h ;
printf("I(DE法)= %f\n",sum) ;
printf("I(厳密)= %f\n",2.0) ;
} 練習:DE法の数値実験
練習:DE法の数値実験
上記のサンプルコードの$h$や積分範囲を調整して、近似の精度がどのように変わるか実験し、その過程でエラーが生じた場合は、その原因について考察しなさい。
半無限区間の積分
積分範囲が$[0,\infty)$の場合は、変換ルールとして $$ \phi(t)=\exp\left( \frac{\pi}{2} \sinh(t) \right) $$ $$ \frac{d\phi}{dt} = \frac{\pi}{2} \cosh(t) \exp\left( \frac{\pi}{2} \sinh(t) \right) $$ が提案されている。これを用いると、 $$ \int_a^{\infty} f(x) dx = \int_{-\infty}^{\infty} f(\phi(t) + a) \frac{d\phi}{dt} dt $$ を台形法で評価すればよい。
 練習:半無限区間の積分
練習:半無限区間の積分
定積分 $$ \int_1^{\infty} \frac{1}{1+x^2} dx $$ を数値的に(できるだけ精度良く)計算してみなさい。
 ヒント
ヒント
$$ \int_1^{\infty} \frac{1}{1+x^2} dx = \frac{\pi}{4} = 0.78539816339744830962 \cdots $$