マガンの群れの紐運動

早川美徳（東北大学　教育情報基盤センター）

概要

大規模なマガンの群れは、揺らぎながら移動する紐のように振る舞うことがある。そして、紐の変形は群れの先頭から後方に波動として伝搬する。フィールドでの計測結果をもとに、こうした集団モード発現の機構を、現象論的なモデルを交えて議論する。

はじめに

ガンやハクチョウ、ツルなどの大型の渡り鳥が、V字型や鈎型といった特徴的な編隊飛行を行うことはよく知られている。こうした渡り鳥は、家族の絆が非常に強いと言われており、家族単位（数羽）で餌場を移動する際にも小さな群れを形成するし、営巣地の近隣では、季節が訪れると、マガンやヒシクイの大規模な群れをしばしば目にすることができる。

同じように集群性が強い鳥で、人間の生活の場でもしばしば目にするスズメやムクドリの群れは、ときに個体数が千を大きく超え、あたかも「雲」のようなクラスターを形成するものの、その運動の様態は、マガンなどとは大きく異なる。

多くの大型の渡り鳥が、V字型や鈎型の隊形を取るのは、前方の個体によって生じる気流を利用することで、飛行にかかるコストが減じられる（楽に飛べる）からであろうと言われている。飛行中に前方の個体が発生する流れ場は、個体の真後ろでは下向きの速度成分（downwash）を、進行方向に対して翼長程度の間隔をおいた斜め後方では、上向きの成分(upwash)が生じる。すなわち、ちょうど翼が少し重なる程度、横方向に間隔を置きながら、一列の並ぶやり方が、各個体にとっても、群れ全体としても、飛行に有利であると見積もられている。

一方、ムクドリなどの群れの形態を決める要因を、流体効果などの物理的要因から、生物の内的情報処理といった可能性までの、いったいどこに求めるべきかは興味深い問題ではあるが、著者の浅薄な知識の範囲では、このことについての信憑性の高い議論は未だ成されていないと思う。

さて、（著者の居住地にも近い）宮城県北部の沼地（伊豆沼、長沼、蕪栗沼等）は、数万羽のマガンが越冬のために集積する場所として知られている。その近隣には、餌場となる、すでに刈り取りの終わった田が広範に分布しており、日中、マガンは数十から数百程度の集団ごとに、落ち穂などをついばんで過ごす。日没が近づくと、こうした集団はほぼ一斉に飛び立ち始め、ねぐらである沼へと向かうが、その途中で、別の餌場から飛び立った群れと合流しながら、ときに視野を覆い尽くすほど大規模な群れが形成される。

比較的長い時間スケールでは、個体が群れに合流したり、群れ同士が融合して、さらに大規模な群れを形成したり、それらが分裂、交差なども繰り返しながら、全体として、非常に動的な振る舞いを呈する。また、突然隊形が崩壊し、再び整列し直すような事例も観察される。

しかしながら、10秒から数分程度の、羽ばたき時間（0.2秒程度）よりは十分長いけれども、隊形そのものが変化するよりは短い時間スケールでは、群れは「運動する一次元的な紐状の構造物」と見なすことができる。

こうした中間的な時間スケールでは、群れを構成する個体数も、群れの大まかな形態も変わらないが、数十個体程度以上の比較的長い「紐」になると、あたかも一端を持って揺らしたロープのように、大きく形を揺らしながら運動しており、しかも、その揺らぎは、群れの前方から後方に向かって伝搬していることが、目視でもはっきりと確認できる。

こうした紐の揺らぎとその伝搬は、比較的大型の群れであれば、気象条件や観察場所などに依らず確認できる。（ただし、定量的なデータはないものの、強風下では、より、揺らぎの程度が大きくなる傾向は見られる。）そのため、波動の励起は、この系に固有の集団的な動力学的特性の現れではないかと直感される。以下では、このマガンの紐状運動と波動伝搬に焦点を当てて、筆者が最近得た知見のいくつかを紹介したい¹。

群れの計測

マガンは、成鳥で体重が2kg、翼開長が1.4m程度と言われており、餌場からねぐらに帰る際には20 m/s 程度の速さで、地上から 50m程度の高度を飛行する。
群れで飛行する場合の隣接する個体同士は、進行方向に凡そ２m程度、横方向には凡そ1m程度の間隔を空けており、飛行高度は急激には変化しないので、荒い近似としては、同一平面内を飛行していると見なせる。ただし、進行方向の間隔については、翼が触れあう程度にまで接近する場合もあれば、かなり大きな間隔を空けて飛行している例も見かける。また、一般的な傾向としては、群れの後方の個体は、僅かではあるが、前方個体よりも高めの位置を取る場合が多く、大型の群れになると、後方が少し持ち上がっているように見える場合もある。

マガンは、１００個体以上が隊列を成して飛行する例も珍しくないので、群れの先頭から末尾までの長さは数１００m程度以上にも及び、その全体を長時間補足するのは容易ではない。

各個体の三次元的な軌跡を推定するために、市販のデジタルカメラ（Canon EOS 5D Mark II）2台を、水平に設置したたわみの小さい金属棒の両端に1mの間隔をおいて固定し、ステレオ撮影する装置を製作した。左右のカメラは電子レリーズで接続し、同時にシャッターを切ることができる。運動を解析する際には、カメラの連射機能とフルハイビジョン動画撮影機能（30fps）を併用した。このとき、フレームの同期は完全ではないものの、時間差は3ms程度以内であることを確認している。

言うまでもなく、ステレオ計測は、左右画像から対応する部分を同定し、画像上の視差から、対象物までの距離Lを推定する方法である。視差は距離に反比例するため、Lがカメラの基線長に較べ十分大きい場合、測定誤差の主要因は視差の算出で生じる。そこで、長距離でもできるだけ検出精度を高めるため、部分画像の相関関数を計算することによって、ピクセル以下の精度で画像のずれを検出できるように工夫した。その結果、静止画の場合、50m先の対象物の移動距離を、（128x128 pixelの部分画像を用いて）3cm程度の精度で検出できることを確認した。原理上、この検出精度は、Lの逆自乗比例して劣化する。また、動画撮影の場合の検出能力は、画素数の低下などの影響で、さらに1/３程度に悪化する。

こうして、100m程度以内の範囲内の個体については、そのサイズと同程度以下の精度で個体の位置を推定できるようになったが、100メートルを大きく超えると、測定誤差がマガンの揺らぎの振幅を上回る程度にまでなってしまうため、以下の方針を取った：

1. 飛行高度や個体間の相互位置などの量は、群れがカメラの頭上近くまで接近した際に、ステレオ計測によって算定する。
2. 遠方から飛来する間、群れの高度は（接近した時と変わらず）一定に保たれていたと仮定し、遠方の個体については、画像から算出される各個体の仰角から、三角測量の原理によって、個体までの距離を推定する。

こうして、カメラから数100m以上離れていても、画像から各個体が識別できる限りにおいて、位置を推定することが可能となる。無論、マガンが常に等高度の平面内を飛行するとは限らないので、こうした解析の妥当性は吟味されねばならない。

こうして得られた時刻tでの平面内のマガンの位置を、最小自乗法で直線フィットし、先頭からn番目の個体の、その直線からの進行方向へのずれをw(n,t)として、時空プロットを作成した例が図1(a)である。

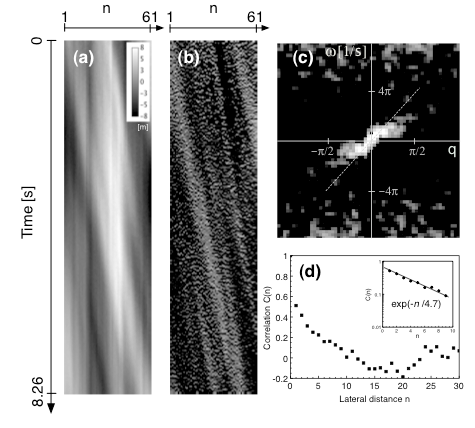
図１　マガンの紐の時空間的な挙動。詳細は本文を参照。

図の濃淡は、直線からの揺らぎ成分の大きさを表しており、さらに、時間的に変化する成分のみを可視化するため、同じデータを時間軸方向に微分したのが図1(b)である。これより、ほぼ等速で、群れの先頭から後方に向けて、波動が伝搬している様子がわかる。その伝搬速度は、およそ 7個体/s 程度で、他の群れでも、ほぼ同様の値を取る。同じデータからパワースペクトルを計算し、波動の分散関係を見ると、計測時間と群れのサイズが限られていることから、やや明瞭さを欠くものの、一方向に進行する音響モード的な励起の存在が見てとれる（図1©）。さらに、波長に換算して６個体分程度よりも高い波数領域では、エネルギー密度が急激に減衰している。

高い波数でのカットオフの存在は、「紐」の運動にある種の特徴的な長さが存在すること意味するが、それをさらに直接的に調べるために、揺らぎ成分の、紐に沿っての相関を求めてみた。紐の局所的な特徴量として$w(n,t)$を長さ方向に微分（差分）を取った量について、その紐に沿っての距離相関C(n)を計算すると、図1(d)に示すように、近距離では指数関数的に減衰しており、その相関距離は、概ね5個体分程度と見積もられた。これは、分散関係のカットオフ波数に相当する長さと言える。このことから、マガンは5個体程度の範囲ではコヒーレントに運動して（揺らいで）おり、ある種のpersistent lengthを持つような紐として扱えるのではないかと考えられる。

比較的長時間の紐の揺らぎ運動とは別に、カメラの近傍の個体に対しては三次元的な軌跡の再構成が可能であるので、撮影条件の良い群れについて、個体の相互位置などを推定した。群れの中のある個体から、後方最近接の個体との相対距離の時間変化を、一つの群れの中のいくつかのペアについて調べてみたところ、飛行方向の相対位置関係は、個体間ごとにかなりの自由度（最大4m程度）があるものの、横方向については、ほぼ1m弱程度の間隔が保たれていた。また、数秒以内の比較的短時間であっても、個体間の相対位置は検出可能な程度に揺らいでいる。こうした相対位置の揺らぎは進行方向にも、横方向にも認められるものの、進行方向の振幅のほうが相対的に大きい。

こうした観察結果から、まず荒い近似として、隣接するマガンの相対位置の変化は、比較的短い時間スケールで調整が行われる横（翼）方向と、進行方向の遅い成分とに、時間スケールの分離が可能ではないかと予想される。もちろん、群れ全体は非常に大きな空間スケールを持つので、隣接個体間の調整機構がそうであったとしても、
群れ全体の運動を考える際に、横方向の変化を「断熱消去」してしまって良いかどうかは自明ではない。事実、大規模な群れでは、紐の「曲がり」や「捻れ」によって、個体の進行方向までもが揺らいでいる様子も観察される。しかしながら、以下のモデリングの議論においては、群れの個体の進行方向も、横方向の間隔も、設定した観察時間の間は、時間的に変動しないという単純化を行った。

マガンは、前方の個体に対して、横方向に翼長程度の間隔を置いた位置に留まろうと「努力」しながら飛行しているとも言える。一方で、進行方向についての位置取りについては、比較的大きな自由度を持つと言える。このことは、これまで提案されてきた流体力学的な議論ともよく符合する。すると、飛行中のマガンは、専ら前方の個体にのみ注意を払って、運動を制御しているはずである。偶然、マガンの列の途中に、下方から、別の個体が割り込みをかける様子を撮影することに成功したが、割り込まれた側の群れの軌跡を解析してみると、割り込み位置よりも前方の個体については、飛行経路に目立った変化は見られなかった一方で、割り込んだ個体よりも後方の個体は、非常に短い時間に、軌跡を横方向にずらす様子が観察された。このことからも、個体間の相互作用は非対称的で、$n$番目の個体は、$n’ < n$番目にのみ影響されていると考えて良いだろう。

モデル

以上の観察結果、あるいは、推論をもとに、群れの先頭から$n$番目の個体の進行方向の座標を$y_n$として、現象論的な運動方程式を
\[
m \ddot{y}_n = F_\textrm{t} + \sum_{\ell<n} F_{n,\ell} - F_\textrm{d}
\]
のように書いてみる。ここで、$m$は個体の質量、 $F_\textrm{t}$は推進力、$F_{n,\ell}$は個体間隔を制御するために生じた有効相互作用力、$F_\textrm{d}$は流体力学的な抵抗力を表す。

各個体は、前方の個体としか相互作用しないと考え、$n$番目の個体が$n-h$番目の個体($h \ge 1$)から
受ける力を$F_{n,n-h}$とおいて、
これが「自然な」個体間距離からのずれで級数展開できると仮定すると、$\alpha_k^{(h)}$を展開係数として
\[
F_{n,n-h} = \sum_{k=1} \alpha_k^{(h)} \left( y_{n-h} – y_n \right)^k
\]
と書けるだろう。ただし、自然な個体間距離をここでは0と置いた（このことで、議論の一般性は失われない）。

マガンの飛行のような高いレイノルズ数（$10^6$程度）領域では、流体からの抵抗力 $F_\textrm{d}$ は
\[
F_\textrm{d} = \frac{1}{2} c_d \rho S \left( \dot{y}_i \right)^2
\]
と近似して良いだろう。ここで$c_d$は抵抗係数、$\rho$は空気の密度、$S$はマガンの断面積である。以下では$\gamma = \frac{1}{2} c_d \rho S $とおく。

このモデルに従うと、相互作用の無い場合は、個体は定常速度 $U_0 = \sqrt{\alpha_0 / \gamma}$ で飛行する。この速度を使って、運動方程式をガリレイ変換 $w = y – U_0 t$した上で、特徴的な時間$T= m/(2\gamma U_0+\beta)$と、長さ$L=a$ ($a$は個体の横方向の距離)を使って、運動方程式を無次元化すると、揺らぎが定常飛行速度より十分小さいときに、$n$番目の個体の運動は、
\[
\frac{d^2 \hat{w}(n,\hat{t}\;)}{d \hat{t}^2} =
\sum_{k \ge 1} \sum_{h \ge 1}
\hat{\alpha}_k^{(h)} \left( \hat{w}(n-h,\hat{t}) – \hat{w}(n,\hat{t})\right)^k
– \frac{d \hat{w}(n,\hat{t}) }{d \hat{t}}
\]
と書ける。ただし、ここで
\[
\hat{\alpha}_k^{(h)} = \frac{m a^{k-1} }{(2 \gamma U_0 + \beta)^2}\alpha_k^{(h)}
\]
である。この単純化のもとでは、$n$は個体の番号という意味に加え、横方向の無次元化された座標と見ることもできる。

このモデルは、相互作用の様式こそ異なるものの、一次元交通流の最適速度モデルと等価と考えられる²。長波長極限で、線形波の伝搬速度は
\[
c_0 = \sum_{h \ge 1} h \alpha_1^{(h)}
\]
で与えられ、
\[
D = c_0^2 – \frac{1}{2} \sum_{h \ge 1} h^2 \alpha_1^{(h)}
\]
が正の場合に線形不安定となる。文献などから、このモデルに現実系での物理的な値を代入し、波動の伝搬速度の実測値を代入することによって、（個体は１つ前方としか相互作用しないと仮定して）、
個体間の有効相互作用パラメータ（仮想的なバネ定数）として$\alpha_1^{(1)}\approx 50$ N/m という値が得られた。また、このとき、系は線形不安定な領域にあること、線形不安定領域となる波数は$q^* \approx 1.8$程度以下と見積もられ、実測の分散関係とも概ね整合すること等の知見が得られた。さらに、中立安定に近い領域にあるため、マガンの群れで見られる波動の後方への伝搬は、一次元交通流の渋滞と同様に、mKdV型のソリトンとして理解できるのはないかと考えている。

文献

¹ Y. Hayakawa, Europhys. Lett. 89 (2010) 48004.

² M. Bando, K. Hasebe, K. Nakanishi, A. Nakayama, A. Shibata, and Y. Sugiyama, Phys. Rev. E 51 (1995) 1035.